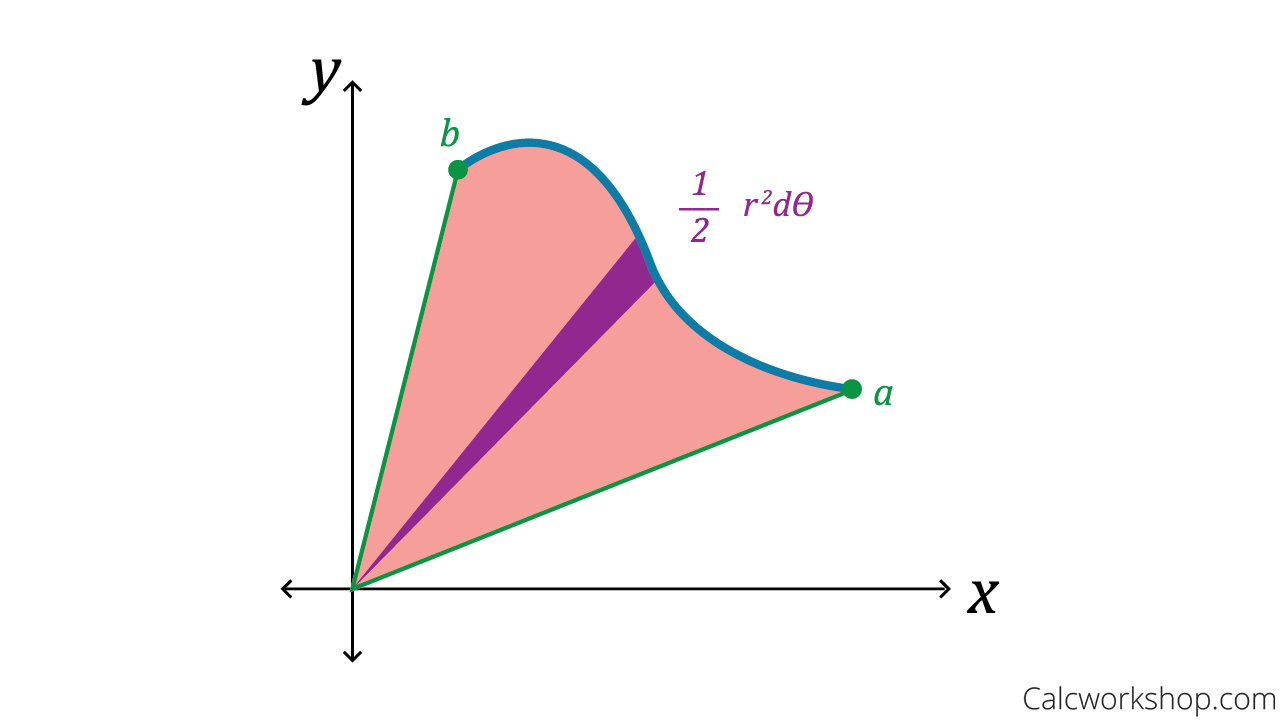
Finding the area enclosed by polar curves is just like finding the area of triangles!
Finding Polar Area
Why?
Well, it has a lot to do with how we subdivide a polar function.
Remember, in our Riemann Sum lesson how we used a technique of subdividing a region into rectangles in order to find the area? Well, in polar coordinates, instead of using rectangles we will use triangles to find areas of polar curves.
Once we understand how to divide a polar curve, we can then use this to generate a very nice formula for calculating Area in Polar Coordinates.
We will realize that we can no longer look at a curve in the typical sense; instead, we must ask the questions:
- How is shaded region enclosed?
- And what are the angle sweeps to enclose such a region?
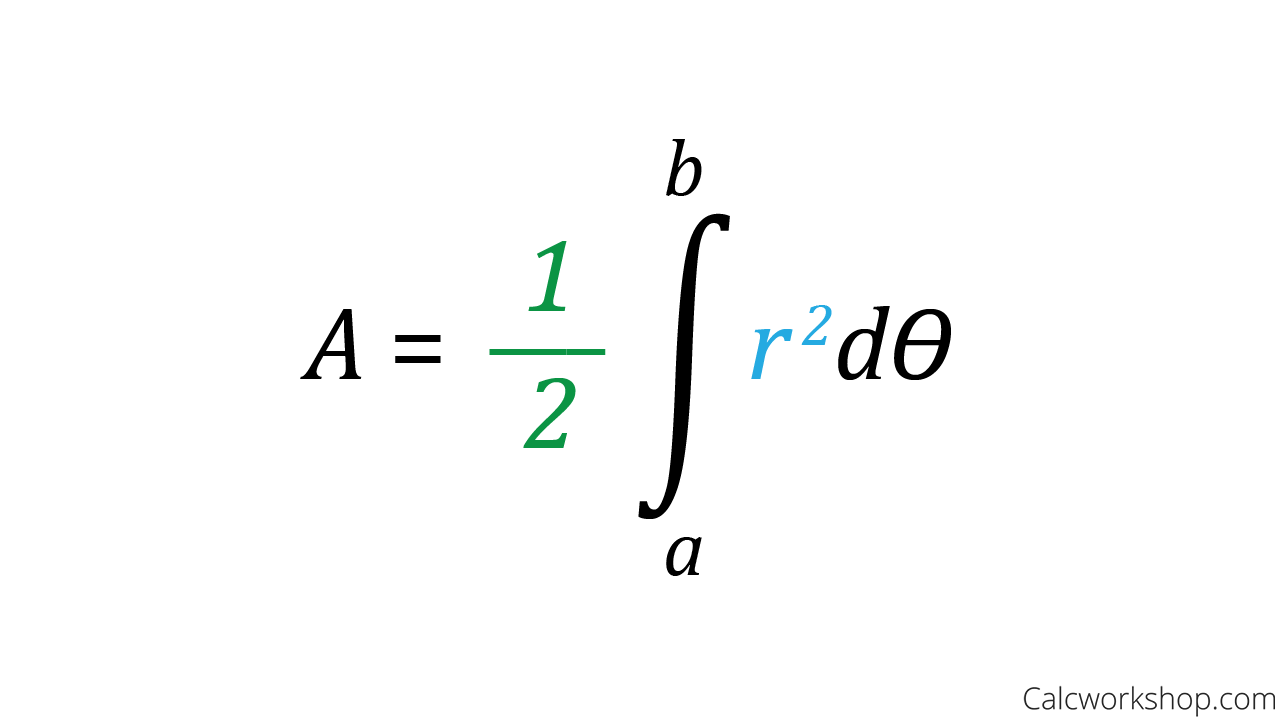
Formula for the Area of a Polar Region
The reason for having to ask these two questions is because of how a polar graph is generated. We start at the pole, or origin, and radiate out.
Therefore, as Paul’s Online Notes accurately states, we must think of the area as being “enclosed by” rather than being “under” as we typically have in the past.
Next, we will use our formula to find the area of all different types of polar curves, and employ our integration strategies to simplify our integrands.
In fact, we will look at how to calculate the area given one polar function, as well as when we need to find the area between two polar curves.
Lastly, we will learn the formula for calculating Arc Length in Polar Coordinates, and look at one example in detail.
Area in Polar Coordinates Video

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.