Sometimes you must break down tasks into parts or steps in order to be more manageable or less intimidating.
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The idea of focusing on one thing and ignoring everything else for a moment helps us see the big picture and allows us to notice how one part can affect the whole.
What Is A Partial Derivative
In mathematics, the process of examining the slope of a surface in only one direction at a time is called partial differentiation.
Partial derivatives calculate the rate of change of a function of several variables with respect to one of those variables while holding the other variables fixed or constant.
In other words, a partial derivative allows only one variable to vary (change) at a time and helps us to analyze surfaces for minimum and maximum points.
And as the graphs below nicely indicate, the partial derivatives are the slopes of the tangent plane in either the \(x\) or \(y\) direction.
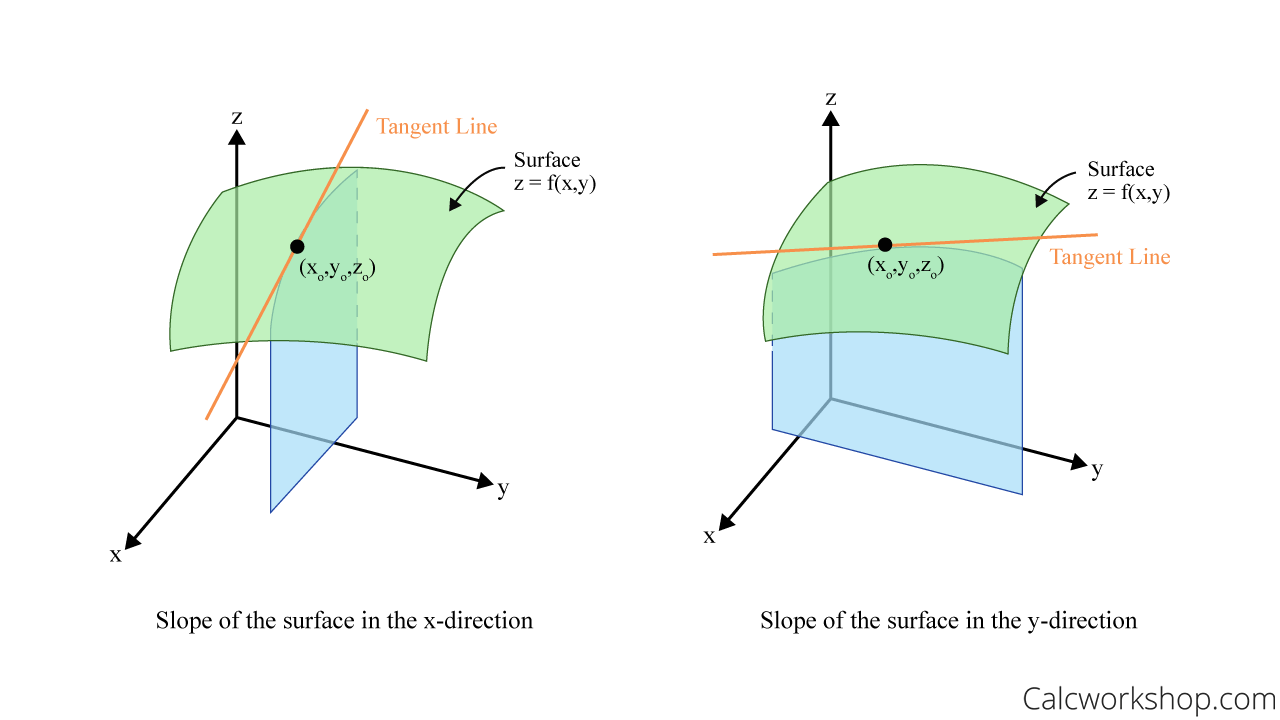
Partial Derivative Slope (Tangent Line)
Derivative Vs Partial Derivative
Wait!
Then what’s the difference between a derivative and a partial derivative?
Well, a derivative from single-variable calculus, called the total derivative, is the rate of change of a compound function. In contrast, a partial derivative measures the rate of change of one particular variable at a time.
So, a total derivative allows for one variable’s change to affect the other, but a partial derivative only allows one variable to change — prohibiting other variables to disturb or disrupt.
Definition & Formula
Let’s examine the formal definition of a partial derivative so we can better understand how to wield its power.
Partial derivatives of a function of two variables states that if \(z = f\left( {x,y} \right)\), then the first order partial derivatives of \(f\) with respect to \(x\) and \(y\), provided the limits exist and are finite, are:
\begin{equation}
\begin{aligned}
&\frac{\partial f}{\partial x}=f_{x}(x, y)=\lim _{\Delta x \rightarrow 0} \frac{f(x+\Delta x, y)-f(x, y)}{\Delta x} \\
&\frac{\partial f}{\partial y}=f_{y}(x, y)=\lim _{\Delta y \rightarrow 0} \frac{f(x, y+\Delta y)-f(x, y)}{\Delta y}
\end{aligned}
\end{equation}
Notice how similar these definitions are to single-variable calculus.
But what is imperative to note is that only one variable is allowed to change at a time.
Symbols
But as we saw with single variable calculus, the limit definition is a bit cumbersome to use, so let’s look at some new notation.
The following notation is consistently used for expressing first partial derivatives.
\begin{equation}
\frac{\partial f}{\partial x}=f_{x}=z_{x}
\end{equation}
\begin{equation}
\frac{\partial f}{\partial y}=f_{y}=z_{y}
\end{equation}
But how do we go about finding the first-order partials?
All we have to do is keep one variable “active” and make the other variable “fixed.”
Let’s look at an example.
Example – How To Take A Partial Derivative
Find the first partial derivatives of \(f\left( {x,y} \right) = {x^2}{y^5} + 3xy\).
First, we will find the first-order partial derivative with respect to x, \(\frac{{\partial f}}{{\partial x}}\), by keeping \(x\) variable and setting y as constant.
\(f\left( {x,y} \right) = {x^2}\underbrace {{y^5}}_a + 3x\underbrace y_b\) , where a and b are constants can be rewritten as follows:
\begin{equation}
f(x, y)=a x^{2}+3 b x
\end{equation}Now, let’s take the derivative with respect to \(x\).
\begin{equation}
\frac{\partial f}{\partial x}=f_{x}=2 a x+3 b
\end{equation}All we have left to do is substitute our \(a = {y^5}\) and \(b = y\) back into the equation and simplify.
\begin{equation}
\begin{aligned}
&\frac{\partial f}{\partial x}=f_{x}=2\left(y^{5}\right) x+3(y) \\
&\frac{\partial f}{\partial x}=f_{x}=2 x y^{5}+3 y
\end{aligned}
\end{equation}Easy, right!
Now, it’s time to find the first-order partial derivative with regards to \(y\), \(\frac{{\partial f}}{{\partial y}}\), by keeping \(y\) variable and setting \(x\) as constant.
\(f\left( {x,y} \right) = \underbrace {{x^2}}_c{y^5} + 3\underbrace x_dy\) , where c and d are constants can be rewritten as follows:
\begin{equation}
f(x, y)=c y^{5}+3 d y
\end{equation}Now, let’s take the derivative with respect to \(y\).
\begin{equation}
\frac{\partial f}{\partial y}=f_{y}=5 c y^{4}+3 d
\end{equation}All we have left to do is substitute our \(c = {x^2}\) and \(d = x\) back into the equation and simplify.
\begin{equation}
\begin{aligned}
&\frac{\partial f}{\partial y}=f_{y}=5\left(x^{2}\right) y^{4}+3(x) \\
&\frac{\partial f}{\partial y}=f_{y}=5 x^{2} y^{4}+3 x
\end{aligned}
\end{equation}
And that’s it.
See, taking partial derivatives is a snap!
Higher Partial Derivatives
But what about higher partial derivatives?
Yes, we can find higher order partial derivatives. In fact, there are four possibilities for the second partial derivative for a function of two variables
- Differentiate twice with respect to x:
- Differentiate twice with respect to y:
- Differentiate first with respect to y, then with respect to x:
- Differentiate first with respect to x, then with respect to y:
\begin{equation}
\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial x^{2}}=f_{x x}
\end{equation}
\begin{equation}
\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^{2} f}{\partial y^{2}}=f_{y y}
\end{equation}
\begin{equation}
\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^{2} f}{\partial x \partial y}=f_{y x}
\end{equation}
\begin{equation}
\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial y \partial x}=f_{x y}
\end{equation}
Clairaut’s Theorem
Please note that \({f_{xy}}\) and \({f_{yx}}\) are called mixed partial derivatives, and thanks to Clairaut’s Theorem, we know they’re equal!
\begin{equation}
f_{x y}=f_{y x}
\end{equation}
Let’s work through an example to demonstrate this fantastic equality.
Example
Using our example from above, let’s find the second partial derivatives of \(f\left( {x,y} \right) = {x^2}{y^5} + 3xy\).
Knowing that…
\begin{equation}
f_{x}=2 x y^{5}+3 y
\end{equation}
\begin{equation}
f_{y}=5 x^{2} y^{4}+3 x
\end{equation}
Let’s find \(\frac{{{\partial ^2}f}}{{\partial {x^2}}}\), the second order partial with respect to \(x\), by taking the derivative of \({f_x}\)with respect to \(x\) by keeping the \(x\) variable active and setting \(y\) as constant.
\({f_x} = 2x\underbrace {{y^5}}_a + 3\underbrace y_b\) , where \(a\) and \(b\) are constants, such that \({f_x} = 2ax + 3b\).
Now, let’s take the derivative with regards to \(x\).
\begin{equation}
f_{x x}=2 a
\end{equation}Lastly, we substitute our \(a = {y^5}\) and back into the equation and simplify.
\begin{equation}
\begin{aligned}
&f_{x x}=2\left(y^{5}\right) \\
&f_{x x}=2 y^{5}
\end{aligned}
\end{equation}Alright, now let’s find \(\frac{{{\partial ^2}f}}{{\partial {y^2}}}\), the second-order partial with respect to \(y\), by taking the derivative of \({f_y}\) with respect to \(y\) by keeping the \(y\) variable active and setting \(x\) as constant.
\({f_y} = 5\underbrace {{x^2}}_c{y^4} + 3\underbrace x_d\) , where \(c\) and \(d\) are constants, such that \({f_y} = 5c{y^4} + 3d\).
Now, let’s take the derivative with respect to \(y\).
\begin{equation}
f_{y y}=20 c y^{3}
\end{equation}Lastly, we substitute our \(c = {x^2}\) and \(d = x\) back into the equation and simplify.
\begin{equation}
\begin{aligned}
&f_{x x}=2\left(y^{5}\right) \\
&f_{x x}=2 y^{5}
\end{aligned}
\end{equation}Okay, so now we want to find our mixed order partials \({f_{xy}}\) and \({f_{yx}}\).
To find \({f_{xy}}\), we take the derivative of \({f_x}\) with respect to \(y\), and to find, we take the derivative of \({f_y}\) with respect to \(x\), as seen below:
\begin{equation}
f_{x}=2 x y^{5}+3 y \Rightarrow f_{x}=2 \underbrace{x}_{a} y^{5}+3 y \Rightarrow f_{x}=2 a y^{5}+3 y
\end{equation}\begin{equation}
\begin{aligned}
&f_{x y}=10 a y^{4}+3 \\
&f_{x y}=10(x) y^{4}+3 \\
&f_{x y}=10 x y^{4}+3
\end{aligned}
\end{equation}\begin{equation}
f_{y}=5 x^{2} y^{4}+3 x \Rightarrow f_{y}=5 x^{2} \underbrace{y^{4}}_{c}+3 x \Rightarrow f_{y}=5 c x^{2}+3 x
\end{equation}\begin{equation}
\begin{aligned}
&f_{y x}=10 c x+3 \\
&f_{y x}=10\left(y^{4}\right) x+3 \\
&f_{y x}=10 x y^{4}+3
\end{aligned}
\end{equation}
See! We’ve just shown the equality of mixed partial derivatives, as \({f_{xy}} = {f_{yx}}\).
Fantastic!
Together we will learn how to represent and find first partial derivatives and higher partial derivatives for multivariable functions by working through a number of examples in detail. And we will fully understand the notation used for partial differentiation and determine the value of partial derivatives at a given point.
Let’s jump on in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.