Multivariable Chain Rule (How-To w/ Step-by-Step Examples!)

What is the multivariable chain rule?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching multivariable chain rule

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

And is it different than the chain rule we learned back in calculus 1?

Well, truth be told, there are several versions of the chain rule, but they are all extremely similar and super easy to use.

Chain Rule Of Differentiation

We learned that the chain rule allows us to differentiate a composite function in single variable calculus.

Recall, a composite function is a function that is inside another function. Similar to how the milk chocolate is encompassed, or inside, the candy-coating shell of an M&M.

So, if $f$ and $g$ are both differentiable functions and $F$ is the composite function defined by $F = f (g (x))$ , then $F$ is differentiable and $F^{'}$ is the product:

$\frac{d y}{d x} = f^{'} (g (x)) \cdot g^{'} (x)$

But this formula, in its current form, only works for single variable functions.

Partial Derivative Chain Rule

Therefore, we will need something similar but a bit more robust for multivariable functions.

Thankfully, we can take our current formula and make a pivotal adjustment to our notation!

$\frac{d y}{d x} = f^{'} (g (x)) \cdot g^{'} (x) = \frac{d f}{d g} \cdot \frac{d g}{d x}$

Why is this important?

Consider the following…

If $z = f (x, y)$ is a differentiable function of $x$ and $y$ , where $x = g (t)$ and $y = h (t)$ are both differentiable functions of $t$ . Then $z$ is a differentiable function of $t$ and

$\frac{d z}{d t} = \frac{\partial f}{\partial x} \frac{d x}{d t} + \frac{\partial f}{\partial y} \frac{d y}{d t}$

Cool!

Example – Single Variable Calculus VS Multivariable Calculus

Let’s look at the implications of this new form as it applies to the following problem.

Suppose $z = 3 x^{2} - y^{2}$ where $x = \sin t$ and $y = \cos t$ . Find $\frac{d z}{d t}$ ?

Well, we can use two different methods. Both are equally great, but I hope to convince you that the second method will be the preferred choice, especially when more variables become involved.

Let’s take a look.

Method #1 – Single Variable

Apply the chain rule, as was done in single-variable calculus.

If $z = 3 x^{2} - y^{2}$ , $x = \sin t$ , $y = \cos t$ , then $z = 3 \sin^{2} t - \cos^{2} t$

Thus…

$\begin{aligned} z = 3 (\sin t)^{2} - (\cos t)^{2} \\ \frac{d z}{d t} = 6 \sin t \cos t - 2 \cos t (- \sin t) \\ \frac{d z}{d t} = 6 \sin t \cos t + 2 \sin t \cos t \\ \frac{d z}{d t} = 8 \sin t \cos t \end{aligned}$

Method #2 – Multivariable

Apply the chain rule for multivariable where we take partial derivatives.

$\frac{d z}{d t} = \frac{\partial f}{\partial x} \frac{d x}{d t} + \frac{\partial f}{\partial y} \frac{d y}{d t}$

If $z = 3 x^{2} - y^{2}$ where $x = \sin t$ , $y = \cos t$ , then:

$\frac{\partial f}{\partial x} = f_{x} = z_{x} = 6 x, \frac{\partial f}{\partial y} = f_{y} = z_{y} = - 2 y, \frac{d x}{d t} = \cos t, and \frac{d y}{d t} = - \sin t$

Next, we have to plug into the formula and simplify.

$\begin{aligned} \frac{d z}{d t} = \frac{\partial f}{\partial x} \frac{d x}{d t} + \frac{\partial f}{\partial y} \frac{d y}{d t} \\ \frac{d z}{d t} = (6 x) (\cos t) + (- 2 y) (- \sin t) \\ \frac{d z}{d t} = 6 x \cos t + 2 y \sin t, where x = \sin t, y = \cos t, then \\ \frac{d z}{d t} = 6 (\sin t) \cos t + 2 (\cos t) \sin t \\ \frac{d z}{d t} = 8 \sin t \cos t \end{aligned}$

As you can see, both methods yield the same result and can be used to check the validity of our answer.

But if there are two ways to find the derivative of a composite function, why do we need the multivariable chain rule?

Great question!

But the answer lies in asking another question…

…what would we do if our function has three, four, or more variables?

Ahh, and this is where method #2 (shown above) really shines, and cements its necessity into our ever expanding mathematical loving hearts.

Multivariable Chain Rule

Now let us consider the situation when $z = f (x, y)$ but this time, each $x$ and $y$ is a function of two variables $s$ and $t$ such that $x = g (s, t)$ and $y = h (s, t)$ .

This means that $z$ is a function of $s$ and $t$ , which complicates matters when trying to compute the derivative using the single-variable method.

Ergo, we do the following to help make things easier.

If $z = f (x, y)$ is a differentiable function of $x$ and $y$ , where $x = g (s, t)$ and $y = h (s, t)$ are differentiable functions of $s$ and $t$ . Then…

$\frac{\partial z}{\partial s} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s} and \frac{\partial z}{\partial t} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t}$

Example – Chain Rule For Two Independent Variables

For instance, assume $z = 3 x^{2} - y^{2}$ where $x = s t^{2}$ and $y = 2 s^{2} t$ . Let’s find $\frac{\partial z}{\partial s}$ and $\frac{\partial z}{\partial t}$ .

First, we will find our partial derivatives.

$\begin{array}{ll} \frac{\partial f}{\partial x} = f_{x} = z_{x} = 6 x & \frac{\partial f}{\partial y} = f_{y} = z_{y} = - 2 y \\ \frac{\partial x}{\partial s} = t^{2} & \frac{\partial y}{\partial s} = 4 s t \\ \frac{\partial x}{\partial t} = 2 s t & \frac{\partial y}{\partial t} = 2 s^{2} \end{array}$

Next, all we have to do is plug into the respective formulas and simplify.

$\begin{aligned} \frac{\partial z}{\partial s} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial s} \\ \frac{\partial z}{\partial s} = (6 x) (t^{2}) + (- 2 y) (4 s t) \\ \frac{\partial z}{\partial s} = 6 x t^{2} - 8 y s t, where x = s t^{2} and y = 2 s^{2} t, then \\ \frac{\partial z}{\partial s} = 6 (s t^{2}) t^{2} - 8 (2 s^{2} t) s t \\ \frac{\partial z}{\partial s} = 6 s t^{4} - 16 s^{3} t^{2} \end{aligned}$

And

$\begin{aligned} \frac{\partial z}{\partial t} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial t} \\ \frac{\partial z}{\partial t} = (6 x) (2 s t) + (- 2 y) (2 s^{2}) \\ \frac{\partial z}{\partial t} = 12 x s t - 4 y s^{2}, where x = s t^{2} and y = 2 s^{2} t, then \\ \frac{\partial z}{\partial t} = 12 (s t^{2}) s t - 4 (2 s^{2} t) s^{2} \\ \frac{\partial z}{\partial t} = 12 s^{2} t^{3} - 8 s^{4} t \end{aligned}$

And that’s it! Using partial derivatives helps to keep things neat and straightforward.

General Formula

Now, this brings us to a more general version of the chain rule so that we can handle functions of any number of variables.

Suppose that $u$ is a differentiable function of $n$ variables $x_{1}, x_{2}, \dots, x_{n}$ and each $x_{j}$ is a differentiable function of $m$ variables $t_{1}, t_{2}, \dots, t_{m}$ . Then for each $i = 1, 2, \dots, m$

$\frac{\partial u}{\partial t_{i}} = \frac{\partial u}{\partial x_{1}} \frac{\partial x_{1}}{\partial t_{i}} + \frac{\partial u}{\partial x_{2}} \frac{\partial x_{2}}{\partial t_{i}} + \dots + \frac{\partial u}{\partial x_{n}} \frac{\partial x_{n}}{\partial t_{i}}$

Don’t worry.

This formula may seem strange, but it’s quite easy to use. We’ll look at several examples in the following video, and I’m confident that you’ll be wielding its power in no time!

Implicit Function Theorem

But we need to discuss one more version of the chain rule, and it involves implicit differentiation!

The Implicit Function Theorem allows us to calculate the derivative implicitly all while using partial derivatives. And the greatest part is that it’s super easy to use!

Implicit Function Theorem for a function $F (x, y)$ .

$\frac{d y}{d x} = - \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} = - \frac{F_{x}}{F_{y}}$

Implicit Function Theorem for a function $F (x, y, z)$ .

$\frac{\partial z}{\partial x} = - \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}} = - \frac{F_{x}}{F_{z}} and \frac{\partial z}{\partial y} = - \frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}} = - \frac{F_{y}}{F_{z}}$

Example

Let’s look at an example to see how this works by finding $y^{'}$ of $x^{3} y^{3} - 2 y = x$ .

As before, let’s compare our two methods – single variable vs. multivariable.

First, we will implicitly take the derivative using our single variable calculus techniques.

Differentiate Implicitly – Product Rule

But now, let’s find the derivative of this same function, using the Implicit Function Theorem.

$\frac{d y}{d x} = - \frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}} = - \frac{F_{x}}{F_{y}}$

First, we will need to collect all terms on one side, so the function is set equal to zero.

$\begin{aligned} x^{3} y^{3} - 2 y = x \\ x^{3} y^{3} - 2 y - x = 0 \\ F (x, y) = x^{3} y^{3} - 2 y - x = 0 \end{aligned}$

Now, we will find our partial derivatives.

$F_{x} = 3 x^{2} y^{3} - 1 and F_{y} = 3 x^{3} y^{2} - 2$

Lastly, we drop our partial derivatives into our formula and simplify to find our solution.

$\begin{aligned} \frac{d y}{d x} = - \frac{F_{x}}{F_{y}} \\ \frac{d y}{d x} = - \frac{(3 x^{2} y^{3} - 1)}{(3 x^{3} y^{2} - 2)} \\ \frac{d y}{d x} = \frac{1 - 3 x^{2} y^{3}}{3 x^{3} y^{2} - 2} \end{aligned}$

Now, wasn’t our new method of using the Implicit Function Theorem pretty awesome and easy?

Yep! I think so too.

Together we will learn how you can apply the multivariable chain rule to the function of two or more variables and evaluate at a point, and how we can take our knowledge of partial derivatives and apply it implicit differentiation.

It’s going to be great, so let’s get to it.

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

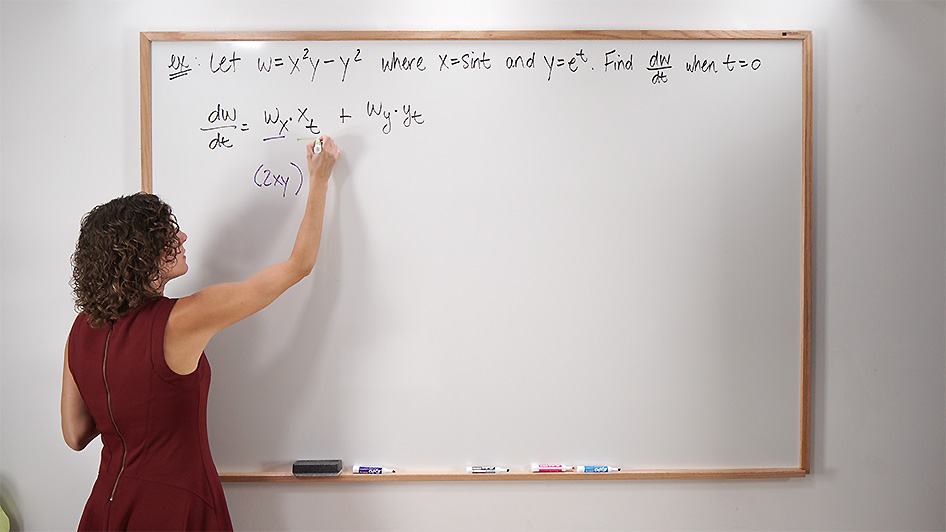
Multivariable-Chain-Rule-Example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,147 Reviews

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Keshav04-24-25 - United Kingdom

I loved it and it helped me get a better understanding of the topics. The ample amount of examples was really helpful to make sure that I understand what I am doing and how to solve various types of problems

Syniah N.04-24-25 - CA, United States

Jen is an exceptional math teacher and a rare find. In a university setting where many instructors prioritize research over teaching, Jen stands out for her ability to explain complex topics in a clear, approachable way.Before discovering this resource, I often felt lost in math classes where instructors wouldn't simplify formal equations for beginners. Jen changed that completely. Thanks to her, I passed Calculus II with an A.I'm truly grateful and highly recommend this resource to anyone struggling with math

Leonardo N.04-20-25 - LA, United States

Calcworkshop is an exceptionally comprehensive mathematics learning platform, spanning from basic algebra to advanced topics like Calculus III, Linear Algebra, and Differential Equations. Its standout feature is the vast number of practice problems, each accompanied by detailed, step-by-step explanations, effectively teaching learners how to approach and solve complex mathematical concepts. The instructor behind Calcworkshop is notably exceptional, delivering lessons with elegance, humility, and clarity, making even challenging topics approachable and enjoyable. Her teaching style combines rigorous mathematical proofs with intuitive analogies, creating an engaging and supportive learning atmosphere. Users consistently experience improved understanding, increased confidence, and significantly better academic performance. Calcworkshop effectively transforms mathematics from an intimidating subject into an exciting and manageable adventure. Ultimately, its unique combination of breadth, depth, engaging instruction, and personalized support makes Calcworkshop unmatched among online math learning resources

Leah04-18-25 - MO, United States

My experience was amazing. I learned so much and it really helped me through my classes.

Dillon04-16-25 - SC, United States

I have been taking my college math courses online because I work full time. It was extremely hard for me to teach myself the material from the textbook without anyone explaining what needed to be done and it was trial, and error and I quickly fell behind in Calculus and Calculus 2. I discovered Calc Workshop a few weeks ago and gave it a try. I went back several courses to refresh what I've learned in the past and I already know more now than I ever did taking the course online. Jen does an amazing job of explaining the material, giving the formulas, and showing where the formulas come from so that you don't HAVE to memorize as much. She also gives helpful tips on how to memorize the rest. I have messaged to ask her several questions and she has responded before the end of the next day every time with exactly the answer I needed. I intend to use Calc Workshop throughout the rest of my college math.

Jon, C.04-06-25 - MD, United States

CalcWorkshop is a premier resource for any student seeking to understand, practice, and succeed within the vast areas of mathematics. I am impressed with the quality of instruction and practice problems offered by Jenn. As a engineering student, I always utilize Calcworkshop as a the "first stop" to really understand and gain confidence in the subject. I credit my success in Calculus to Jenn and CalcWorkshop and making me "smarter than the average bear."

Sayida S.04-03-25 - PA, United States

I absolutely love this subscription. At first I was iffy about spending the money, but in the long term it is so worth it. I started watching Jenn almost 3/4ths into my calc 2 class, and I a confidently say I understand the depths to each topic. Before, with my professor I felt that I only understood surface level of each topic. But after the CalcWorkshop videos, I have acronyms, tips, and knowledge I walk away with, that I didn't have before. Genuinely cannot wait to keep using this website for my future endeavors, minoring in Mathematics!

Gina K.03-30-25 - WA, United States

My experience was great! I needed help studying for my math class, but I wasn't sure how-until an ad for this popped up on my YouTube. After watching the ad, I was convinced, so I subscribed to CalcWoskop. I'm so happy I did because it helped me so much with my class! I learned a lot that I couldn't grasp from my college lectures, and this was the perfect solution.

Maria03-26-25 - AB, Canada

I found Jenn's videos near the end of my discrete math class, so I only had a month to go through all of her discrete math lessons to study for my exam. I'm sure I would have aced it if I had more time but I got a pretty good grade considering I thought I would fail.So happy to be done that class!As advertised, Jenn is very thorough and doesn't skip steps, she lets you know exactly how she gets from a to b or she will refer you to other videos where she teaches the techniques she's using more in depth. This was extremely valuable to me, being a mature student taking advanced math while not remembering basic algebra.And it was fun to understand and solve complex problems vs memorize proof structures.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

Syniah N.04-24-25 - CA, United States

Leonardo N.04-20-25 - LA, United States

Dillon04-16-25 - SC, United States

See more reviews on Shopper Approved