Wouldn’t it be great to be able to find the slope of a surface in any direction?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Thanks to Directional Derivatives and the Gradient Vector, we can!
Imagine you are out on a hike. As you plan your upward and downward descent along the undulating terrain, you constantly have to navigate varying slopes along your path.
In other words, you must constantly ask yourself, “what is the rate of change in the direction I’m traveling?”
Think of it this way.
As you look about over the rolling hills, your line of sight creates a curve for which you would travel, and you plan your next step. As you scan the landscape, you change your visual direction; thus, changing the curve you will travel.
What Is Directional Derivative?
Now, as we know, the partial derivatives
But they can only tell us the rate of change parallel to the
What about the slope in any direction?
We begin by letting
Next, we need to pick a direction of where we hope to travel or walk. So, we let our fixed direction be the unit vector
Then, the directional derivative of
Directional Derivative Formula
More generally speaking, the rate of change of
Okay, so there’s a lot to unpack in this definition, so let’s work through an example to help make sense of things.
And don’t worry, we’ll talk about the gradient vector,
Example
Find the directional derivative of
Okay, so first, we will find our unit vector by dividing each component of vector
by its magnitude.
So, now that we have our unit vector
, let’s compute our gradient vector . The gradient vector, denoted
or , read “del f”, is a vector valued function such that…
Therefore, for our function
, the gradient is:
Now, let’s substitute our given point
into and evaluate.
Lastly, we plug our values into our directional derivative formula and simplify.
Awesome!
But what did we find?
The value represents the rate of change!
So, as you can see, the directional derivative allows us to find the slope in the same direction we desire.
Cool!
But there’s more!
Calculate The Directional Derivative
Suppose the direction of a directional derivative is described by the angle
Example
For example, suppose we were asked to find the directional derivative of
Since we are not given a unit vector but an angle of inclination of
, we will use our new handy expression to find our unit vector.
Now, we proceed by finding our partial derivatives at our given point and substituting them into our directional derivative formula.
Perfect!
Gradient Vector
Now, let’s look a bit more closely at the gradient vector.
- First, the gradient vector is normal to all level curves. So, when we let
- Secondly, the gradient tells us in what direction this maximum change is occurring, and its magnitude tells us how to find the maximum rate of change of a function at a given point.
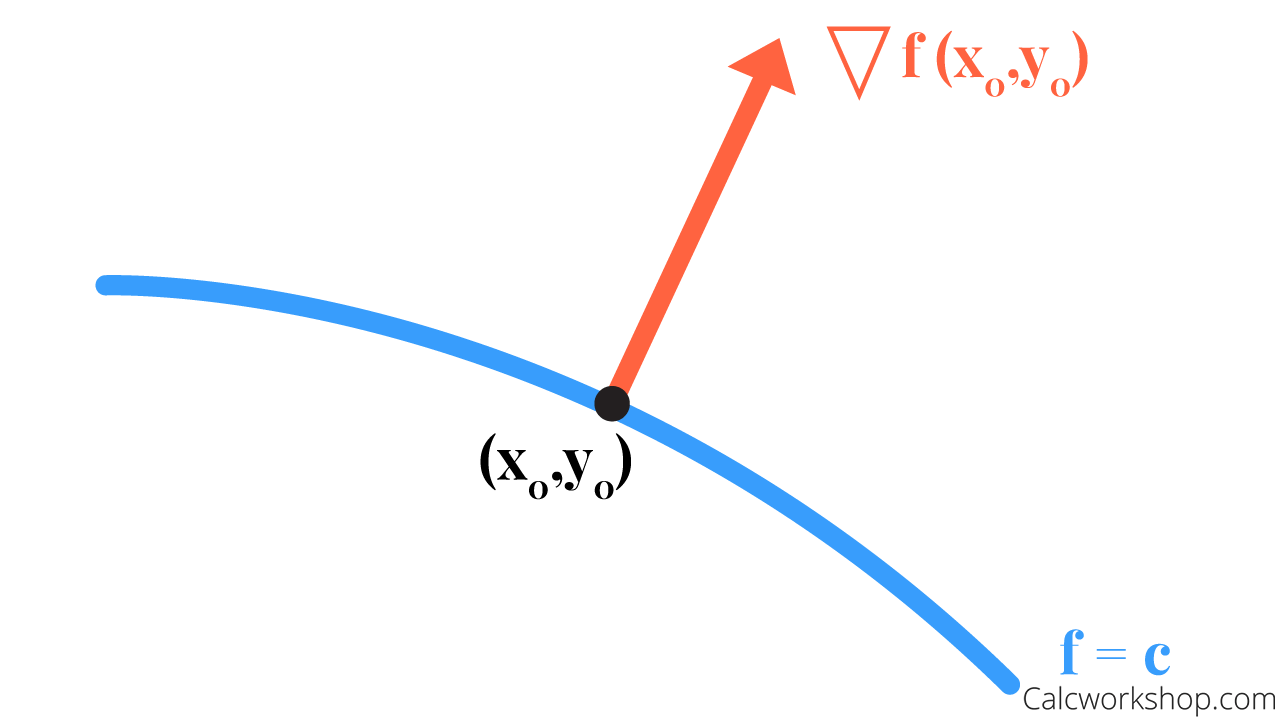
Gradient Vector Perpendicular Level Curve
This means the function
increases most rapidly at in the direction of the gradient with a rate of and decreases most rapidly in the oppositive direction with a rate of .
Example
For example, let’s find a vector indicating the direction of most rapid increase of
Okay, so the vector that points in the direction of most rapid increase is the gradient vector:
So, let’s take our first order partial and evaluate the gradient vector at our given point.
Now that we have found the vector indicating the direction of steepest increase, we need to find the rate of change in that direction by calculating its magnitude
.
And that’s it!
Easy, right?
Together we will learn how a directional derivative is a value that represents a rate of change and how to find the directional derivatives both geometrically and algebraically. We will then take a closer look at the Gradient Vector, as it signifies a vector that points to the direction of the steepest ascent of a curve.
We will work through examples of how to calculate and draw gradient vectors, as they are orthogonal to level curves, use the gradient to determine maximum and minimum steepness of a surface, and how the gradient vector helps us understand the tangent plane to a level surface.
There’s so much to discover so let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.