Did you know that another term for dot product is the inner product?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
By extending the concept of the dot product to general vector spaces, we can incorporate the set of polynomials, matrices, and continuous functions just like we would for a Euclidean \(\mathrm{n}\)-space.
But what does all of this mean? What’s a dot product?
Understanding Dot Product with Examples
A dot product, sometimes called the scalar product, is the product or multiplication of two vectors and is written with a raised dot, such as \(\vec{a} \cdot \vec{b}\).
Let’s look at an example.
Suppose we are asked to find the inner product of the following two vectors:
\begin{aligned}
\vec{a} & =\langle 8,-5\rangle \\
\vec{b} & =\langle 2,1\rangle
\end{aligned}
All we have to do is multiply each component and add their products
\begin{aligned}
\vec{a} \cdot \vec{b} & =\langle 8,-5\rangle \cdot\langle 2,1\rangle \\
& =(8)(2)+(-5)(1) \\
& =16-5 \\
& =11
\end{aligned}
Notice that the inner product yields a scalar value and not a vector.
This is extremely important to note because a vector has both direction and magnitude (length), whereas the inner product is not a vector but a number only.
Dot Product of Column Matrices
But how do we apply the dot product to vectors written as column matrices?
Don’t worry. The process is still the same because of the following property.
If \(\vec{a}=\left[\begin{array}{c}a_{1} \\ \vdots \\ a_{n}\end{array}\right]\) and \(\vec{v}=\left[\begin{array}{c}b_{1} \\ \vdots \\ b_{n}\end{array}\right]\) then \(\vec{a} \cdot \vec{b}=(\vec{a})^{T} \cdot \vec{b}=\left[\begin{array}{lll}a_{1} & \cdots & a_{n}\end{array}\right]\left[\begin{array}{c}b_{1} \\ \vdots \\ b_{n}\end{array}\right]=a_{1} b_{1}+\cdots+a_{n} b_{n}\)
For example, let’s find the inner product of \(\vec{a}=\left[\begin{array}{c}-1 \\ 2 \\ -5\end{array}\right]\) and \(\vec{b}=\left[\begin{array}{c}-3 \\ 3 \\ 2\end{array}\right]\)
Well, all we have to do is transpose the first vector and add the product of the corresponding entries.
\begin{aligned}
\vec{a} \cdot \vec{b} &= (\vec{a})^{T} \cdot \vec{b} \\
&= \left[\begin{array}{lll}
-1 & 2 & 5
\end{array}\right]\left[\begin{array}{c}
-3 \\
3 \\
2
\end{array}\right] \\
&= (-1)(-3)+(2)(3)+(5)(2) \\
&= 19
\end{aligned}
Easy!
Properties of Dot Product
And this leads us to some very beneficial properties.
If \(\vec{m}, \vec{n}\), and \(\vec{p}\) are vectors in \(\mathbb{R}^{n}\) and if we let \(\mathrm{c}\) be a scalar, then:
\(\vec{m} \cdot \vec{n}=\vec{n} \cdot \vec{m}\)
\((\vec{m}+\vec{n}) \cdot \vec{p}=\vec{m} \cdot \vec{p}+\vec{n} \cdot \vec{p}\)
\((\overrightarrow{c m}) \cdot \vec{n}=c(\vec{m} \cdot \vec{n})=\vec{m} \cdot(\overrightarrow{c n})\)
\(\vec{m} \cdot \vec{m} \geq 0\) and \(\vec{m} \cdot \vec{m}=0\) if and only if \(\vec{m}=\overrightarrow{0}\)
\(\vec{m} \cdot \vec{n}=\|\vec{m}\| \cdot\|\vec{n}\| \cos \theta\), where \(\|\vec{m}\|\) is the length of vector \(\vec{m},\|\vec{n}\|\) is the length of vector \(\vec{n}\), and \(\theta\) is the angle between vectors \(\vec{m}\) and \(\vec{n}\).

Inner Product of Two Vectors
Determining a Vector’s Length
But how do we find a vector’s length, sometimes called the magnitude or norm?
By using the Pythagorean theorem, of course!

How to find the Norm of a Vector
If the length of a vector in \(\mathbb{R}^{2}\) is the square root of the sum of the square of the \(\mathrm{x}\) and \(\mathrm{y}\) components, as seen above, then we can extend this concept to any vector in \(\mathbb{R}^{n}\) to be
\begin{aligned}
\|\vec{a}\| &= \sqrt{a_{1}^{2}+a_{2}^{2}+\cdots+a_{n}^{2}} \\
\|\vec{a}\|^{2} &= (\sqrt{\vec{a} \cdot \vec{a}})^{2} \\
&= \vec{a} \cdot \vec{a}
\end{aligned}
Application of Norm to Matrices
And as the norm measures the magnitude of things, it should be noted that we can find the norm or length of a matrix \(\mathrm{A}\) in a vector space by as \(\|A\|=\sqrt{\langle A, A\rangle}=\sqrt{\operatorname{tr}\left(A^{T} A\right)}\)
For example, suppose \(A=\left[\begin{array}{ll}4 & 3 \\ 2 & 1\end{array}\right]\). Let’s find then the norm \(\|A\|\).
First, we will find the trace of the inner product of \(\mathrm{A}\) and \(\mathrm{A}\).
\begin{aligned}
\operatorname{tr}\left(\left[\begin{array}{ll}
4 & 3 \\
2 & 1
\end{array}\right]^{T}\left[\begin{array}{ll}
4 & 3 \\
2 & 1
\end{array}\right]\right) &= \operatorname{tr}\left(\left[\begin{array}{ll}
4 & 2 \\
3 & 1
\end{array}\right]\left[\begin{array}{ll}
4 & 3 \\
2 & 1
\end{array}\right]\right) \\
&= \operatorname{tr}\left[\begin{array}{cc}
22 & 15 \\
10 & 7
\end{array}\right] \\
&= 22+7 \\
&= 29
\end{aligned}
Next, we apply the square root to find
\begin{aligned}
\|A\| &= \sqrt{\operatorname{tr}\left(A^{T} A\right)} \\
&= \sqrt{29}
\end{aligned}
Cool, right?
Creating Unit Vectors
And did you know that we can utilize the length of a vector to create a unit vector? A unit vector is a vector whose length is 1, and we can create unit vectors by simply dividing a nonzero vector by its length. This process is sometimes referred to as normalizing.
\begin{align*}
\vec{u}=\frac{\vec{a}}{\|\vec{a}\|}
\end{align*}
For example, let \(\vec{a}=(2,-2,1,0)\). Find a unit vector \(\vec{u}\) in the same direction as \(\vec{a}\)
First, we will calculate the norm or length of \(\vec{a}\)
\begin{aligned}
\|\vec{a}\| &= \sqrt{(2)^{2}+(-2)^{2}+(1)^{2}+(0)^{2}} \\
&= \sqrt{9} \\
&= 3
\end{aligned}
Now we divide each component of the vector by its magnitude to obtain the unit vector.
\begin{aligned}
\vec{u} &= \frac{\vec{a}}{\|\vec{a}\|} \\
&= \frac{(2,-2,1,0)}{3} \\
&= \left(\frac{2}{3}, \frac{-2}{3}, \frac{1}{3}, 0\right) \\
&\text{ or } \\
\vec{u} &= \left[\begin{array}{c}
2 / 3 \\
-2 / 3 \\
1 / 3 \\
0
\end{array}\right]
\end{aligned}
Finding the Angle Between Vectors
Alright, so now that we know how to find the length of a vector, we can use this knowledge to find angles.
Remember how one of the properties listed above says \(\vec{m} \cdot \vec{n}=|| \vec{m}\|\cdot || \vec{n}\| \cos \theta\) ? Well, let’s put this into action and determine the angle between two vectors with the following example.
Assume \(\vec{a}=\left[\begin{array}{l}2 \\ 5\end{array}\right]\) and \(\vec{b}=\left[\begin{array}{c}5 \\ -2\end{array}\right]\). Let’s use the inner product formula to find the angle between the vectors.
First, we will find the norm of \(\vec{a}\) and \(\vec{b}\)
\begin{aligned}
\|\vec{a}\| &= \sqrt{(2)^{2}+(5)^{2}} \\
&= \sqrt{29} \\
\|\vec{b}\| &= \sqrt{(5)^{2}+(-2)^{2}} \\
&= \sqrt{29}
\end{aligned}
Next, we will find the inner product.
\begin{aligned}
\vec{a} \cdot \vec{b} &= (\vec{a})^{T} \cdot \vec{b} \\
&= \left[\begin{array}{ll}
2 & 5
\end{array}\right]\left[\begin{array}{c}
5 \\
-2
\end{array}\right] \\
&= 2(5)+5(-2) \\
&= 0
\end{aligned}
Now we will substitute our values into our formula and solve for theta.
\begin{aligned}
\vec{a} \cdot \vec{b} &= \|\vec{a}\| \cdot\|\mid \vec{b}\| \cos \theta \\
0 &= (\sqrt{29})(\sqrt{29}) \cos \theta \\
0 &= 29 \cos \theta \\
0 &= \cos \theta \\
\theta &= \cos ^{-1}(0) \\
&= 90^{\circ}
\end{aligned}
Plus, if we plot these two vectors, we can indeed see that the vectors are perpendicular to each other.
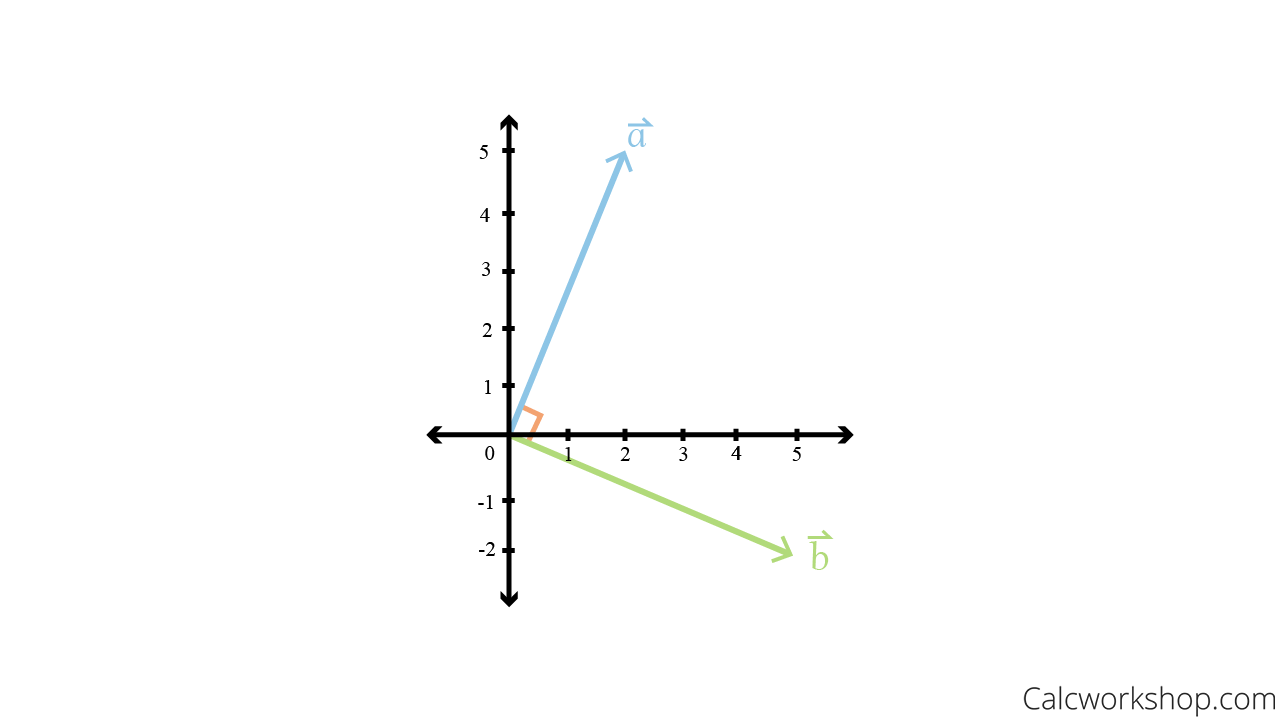
Inner Product – Orthogonality Graph
Orthogonality and Inner Product
And when the inner product is zero, the two vectors are said to be orthogonal (i.e., perpendicular).
This is an essential concept! Two vectors \(\vec{a}\) and \(\vec{b}\) are orthogonal (i.e., \(\vec{a} \perp \vec{b}\) ) if and only if \(\|\vec{a}+\vec{b}\|=\|\vec{a}\|^{2}+\|\vec{b}\|^{2}\), as we will prove in our video lesson.
Orthogonal Complement
Consequently, if a vector \(\vec{a}\) is orthogonal to every vector in a subspace \(\mathrm{W}\) of \(\mathbb{R}^{n}\), then \(\vec{a}\) is said to be orthogonal to \(\mathrm{W}\). And the set of all vectors \(\vec{a}\) that are orthogonal to \(\mathrm{W}\) is called the orthogonal complement of \(\mathrm{W}\) and is denoted by \(W^{\perp}\), which is read as “W perp”
For example, suppose \(L\) consists of all vectors that orthogonal to vector \(\mathbb{R}^{n}\) in plane \(\mathrm{W}\), and \(\mathrm{W}\) consists of all vectors orthogonal to all the vectors in \(\mathrm{L}\), then the orthogonal complement of a line \(\mathrm{L}\) in \(\mathbb{R}^{3}\) is the perpendicular plane \(W^{\perp}\)
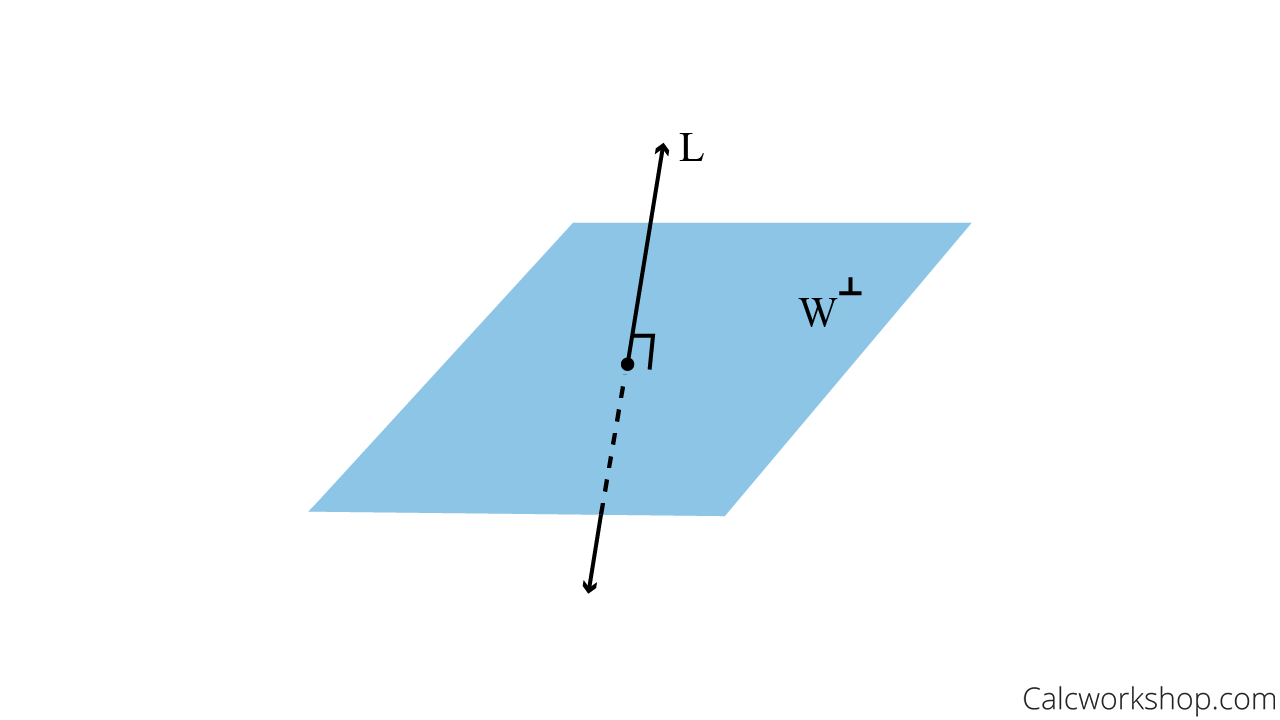
How to Find W Perp for Planes
Implications of Orthogonal Complement
So, this has some beneficial implications:
A vector \(\vec{x}\) is in \(W^{\perp}\) if an only if \(\vec{x}\) is orthogonal to every vector in a set that spans \(\mathrm{W}\).
\(W^{\perp}\) is a subspace of \(\mathbb{R}^{n}\)
\(\left(W^{\perp}\right)^{\perp}=W\)
\(\operatorname{dim}(W)+\operatorname{dim}\left(W^{\perp}\right)=n\)
If the subspace \(\operatorname{span}(v)\) is a line in \(\mathbb{R}^{2}\), then the orthogonal complement of \(\operatorname{span}(v)\) is a line.
If the subspace \(\operatorname{span}(v)\) is a line in \(\mathbb{R}^{3}\), then the orthogonal complement of \(\operatorname{span}(v)\) is a plane.
If \(\mathrm{A}\) is an \(n \times n\) matrix, then the orthogonal complement of the row space of \(\mathrm{A}\) is the nullspace of \(A\), and the orthogonal complement of the column space of \(\mathrm{A}\) is the nullspace of, such that
\((\operatorname{Row} A)^{\perp}=\operatorname{Nul} A \quad\) and \(\quad(\operatorname{Nul} A)^{\perp}=\operatorname{Row} A\) \((\operatorname{Col} A)^{\perp}=\operatorname{Nul} A^{T} \quad\) and \(\quad\left(\operatorname{Nul}^{T}\right)^{\perp}=\operatorname{Col} A\)
Next Steps
And
In this lesson, you will:
- Learn how to find the inner product and norm of a vector
- Discuss orthogonality of vectors to determine the orthogonal distance between two vectors
- Investigate orthogonal complements, “W-perp”
- Learn how to find the basis for a set of orthogonal vectors
- See the connection between orthogonality and the row space, column space, and the null space
Jump right in and start exploring!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.