Did you know that you use modular arithmetic daily?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
The Clock
Every time you think about “time,” you use modular arithmetic because it deals with cycles of integers and remainders just like a clock.
For example, suppose your clock reads 9:00 (am/pm is not important).
What will the clock show in 10 hours?
Well, 9 + 10 = 19, but “19 o’clock” is not something that can be displayed on a clock with the numbers 1 to 12.
So, what do we do?
We subtract 12 from 19 and proudly say that the clock will show 7:00.
This is the idea behind modular arithmetic, which is sometimes referred to as “clock arithmetic” because 19 mod 12 = 7 mod 12, where 7 represents the remainder when 19 is divided by 12. You can review more history behind the idea at the Institute for Advanced Studies.
How To Do Modular Arithmetic
This means that modular arithmetic finds the remainder of a number upon division!
Example #1
What is 16 mod 12?
Well 16 divided by 12 equals 1 remainder 4. So the answer is 4!
Example #2
What about 15 mod 2?
Here, 15 divided by 2 equals 7 remainder 1, so the solution is 1!
Example #3
And if you have 18 mod 9?
Alright, so we know that 18 divided by 9 equals 2 remainder 0, so that means 18 mod 9 is equivalent to 0!
So, what have we learned?
But just like we say with divisibility, the remainder must be positive.
Example #4
For this problem, suppose we wanted to evaluate -97 mod 11.
Well, -97 divided by 11 equals -8 remainder -9.
But since this remainder is negative, we have to increase our quotient by 1 to say -97 divided by 11 equals -9 remainder 2, as 11(-9) + 2 = -97!
Therefore, -97 mod 11 equals 2!
Modular Congruence
Now, in number theory, we often want to focus on whether two integers say a and b, have the same remainder when divided by m. This is the idea behind modular congruence.
Congruence is nothing more than a statement about divisibility and was first introduced by Carl Friederich Gauss.
In other words, a congruence modulo asks whether or not a and b are in the same equivalence class.
Congruence Modulo Property
Equivalence Class
What’s an equivalence class?
It’s best explained with an example.
Suppose we want to find the equivalence classes of mod 3. Well, we know that “mod” means we are interested in remainders, so what are the possible remainders when a number is divided by 3?
It’s 0, 1, or 2!
Here’s how.
Okay, so the remainders of 0, 1, or 2 comprise the equivalence classes for mod 3, which we write as [0], [1], and [2].
But let’s look a bit deeper and find all the values within each class (partition).
Here’s a trick, start by listing the equivalence classes as separate columns and then start at zero and keep writing numbers consecutively, wrapping to the next row, as shown below.
Equivalence Class Mod 3
This means that [0] = {…-6,-3,0,3,6,9,…} and [1] = {…-5,-2,1,4,7,10,…} and [2] = {…-5,-1,2,5,8,11,…}
Why?
Because every integer within the equivalence class has the same remainder when divided by 3!
Notice the following:
- 6/3 = 2 with remainder 0.
- 7/3 = 2 remainder 1.
- 8/3 = 2 remainder 2.
Congruence Modulo — Examples
So, now let’s see how equivalence classes help us determine congruence.
If n is a positive integer then integers a and b are congruent modulo n if they have the same remainder when divided by n. Another way to think of congruence modulo, is to say that integers a and b congruent modulo n if their difference is a multiple of n.
For example, 7 and 4 are congruent modulo 3 because not only are they in the same equivalence class, but their difference 7-4 = 3, is a multiple of 3 (i.e., 3 divides 3), as shown below.
Problem #1
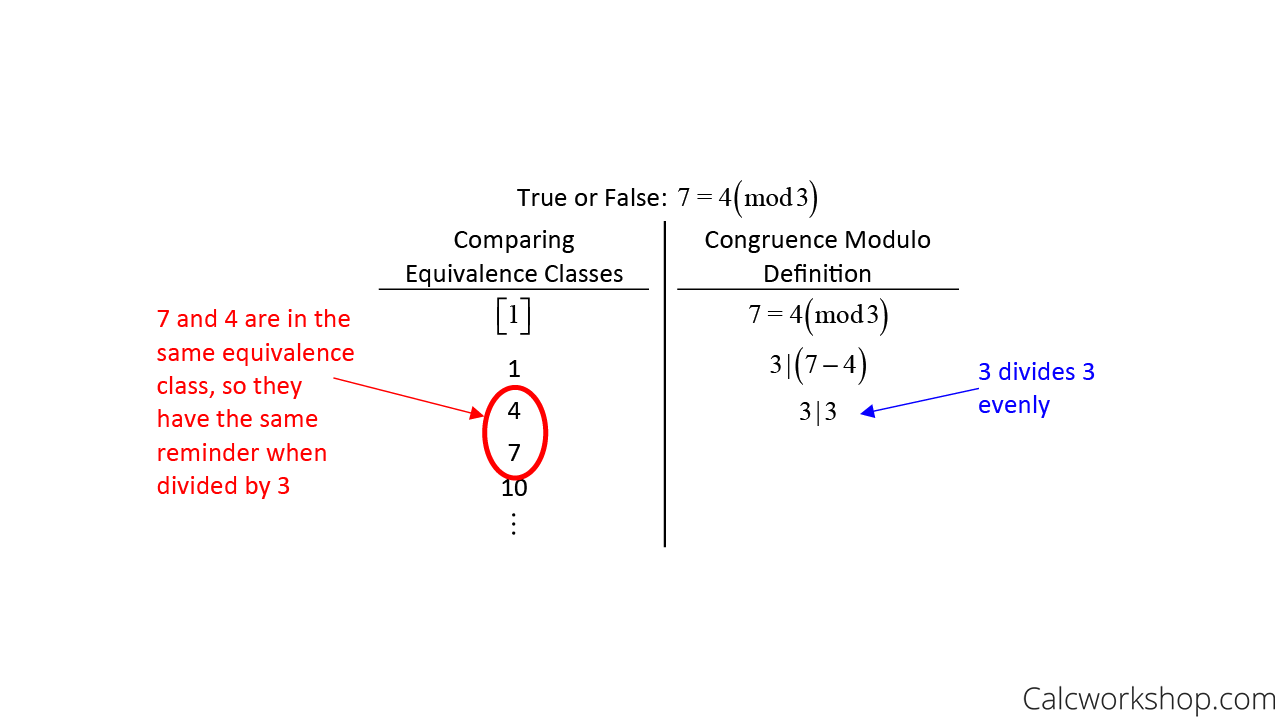
Determine Congruence — Example
But 11 and 6 are not congruent modulo 3 because they are not in the same equivalence class and their difference, 11-6 = 5, is not a multiple of 3, as illustrated below.
Problem #2
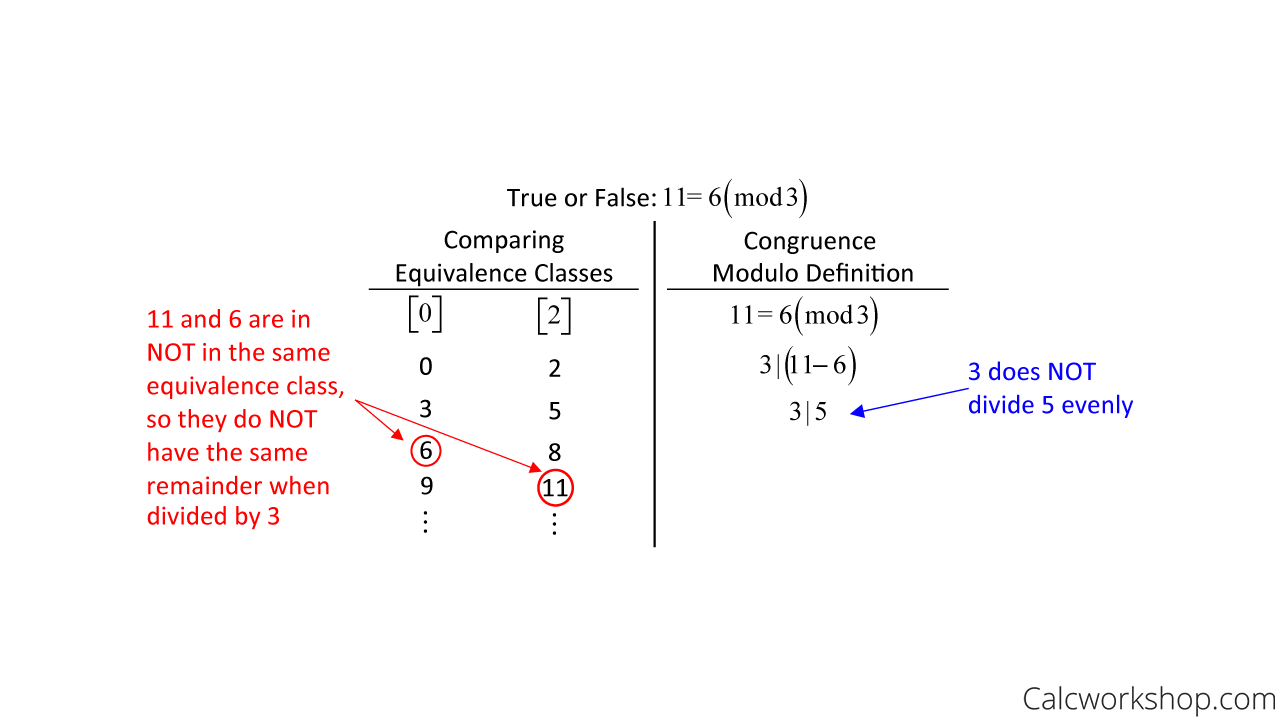
Verify Incongruence — Example
So, what have we learned? If the remainders are equal to each other, then they are congruent! And the following theorem highlights this very idea:
Congruence Property
And this leads us to several vital theorems for congruence modulo.
Modular Arithmetic Properties
In our lesson, we will work through several proofs for these essential theorems, as they are pivotal in our understanding of equivalence relations (future lesson) and allow us to define arithmetic operations.
For example, let’s find:
- (7+9)(mod 11)
- (7)(9)(mod 11)
Modular Arithmetic Multiplication Addition
Arithmetic Modulo
And this leads us to Arithmetic Modulo m, where we can define arithmetic operations on the set of non-negative integers less than m, that is, the set {0,1,2,…,m-1}.
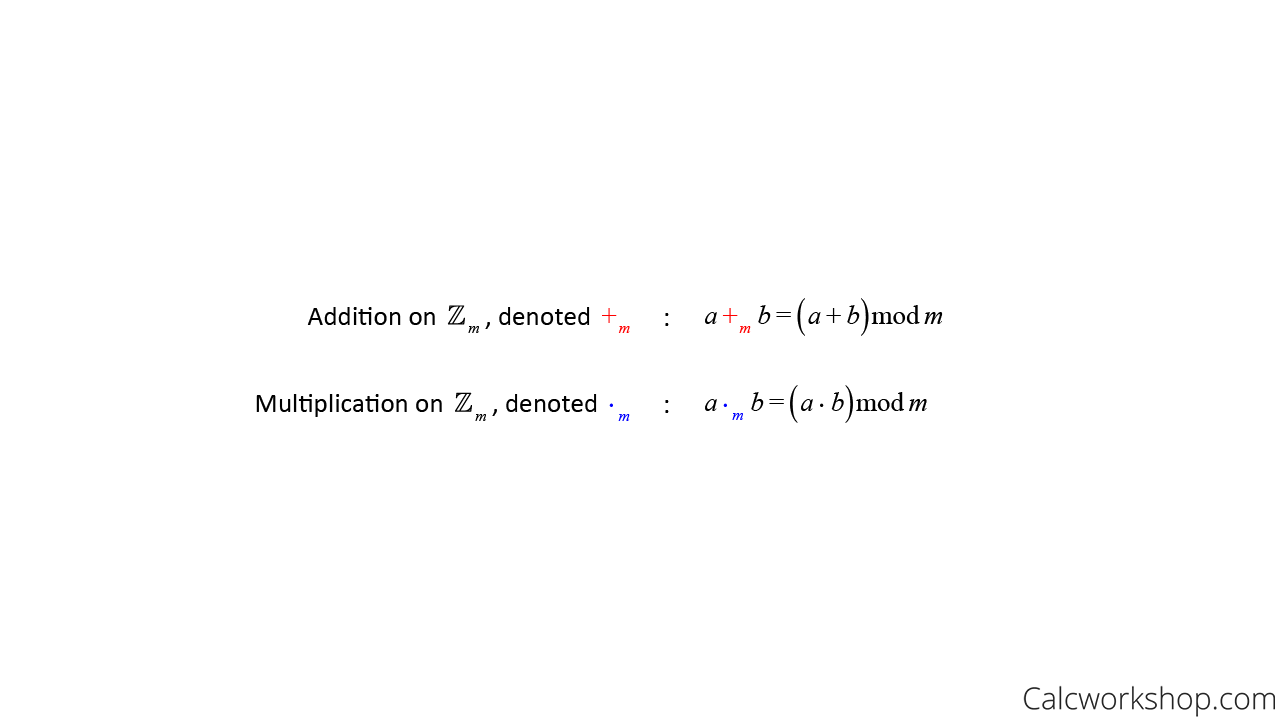
Arithmetic Modulo M Properties
The definition of addition and multiplication modulo follows the same properties of ordinary addition and multiplication of algebra.
The following properties are all satisfied.
- Closure
- Commutativity
- Associativity
- Identity
- Inverse
- Distributivity
Together we will work through countless examples of modular arithmetic and the importance of the remainder and congruence modulus and arithmetic operations to ensure mastery and understanding of this fascinating topic.
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 19 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.