Did you know that we can use the fundamental theorem of arithmetic to help us find the greatest common divisor?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Primes (and why they’re important)
The Fundamental Theorem of Arithmetic states that every integer greater than one can be written uniquely as a prime or as the product of two or more primes. And a prime number is an integer greater than one where its only factors are one and itself. Otherwise, an integer is composite.
Here’s a list of common prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,…etc.
What’s important to note is that primes are the building blocks of positive integers, as they can be used to represent any positive integer,
The most traditional way of identifying prime factors is to create a factor tree, which is a diagram with branches that go through the factoring steps. The key to using a tree diagram is to keep factoring until all the dangling “fruit” are prime numbers.
Example
For instance, let’s find the prime factorization of 96 using a factor tree.
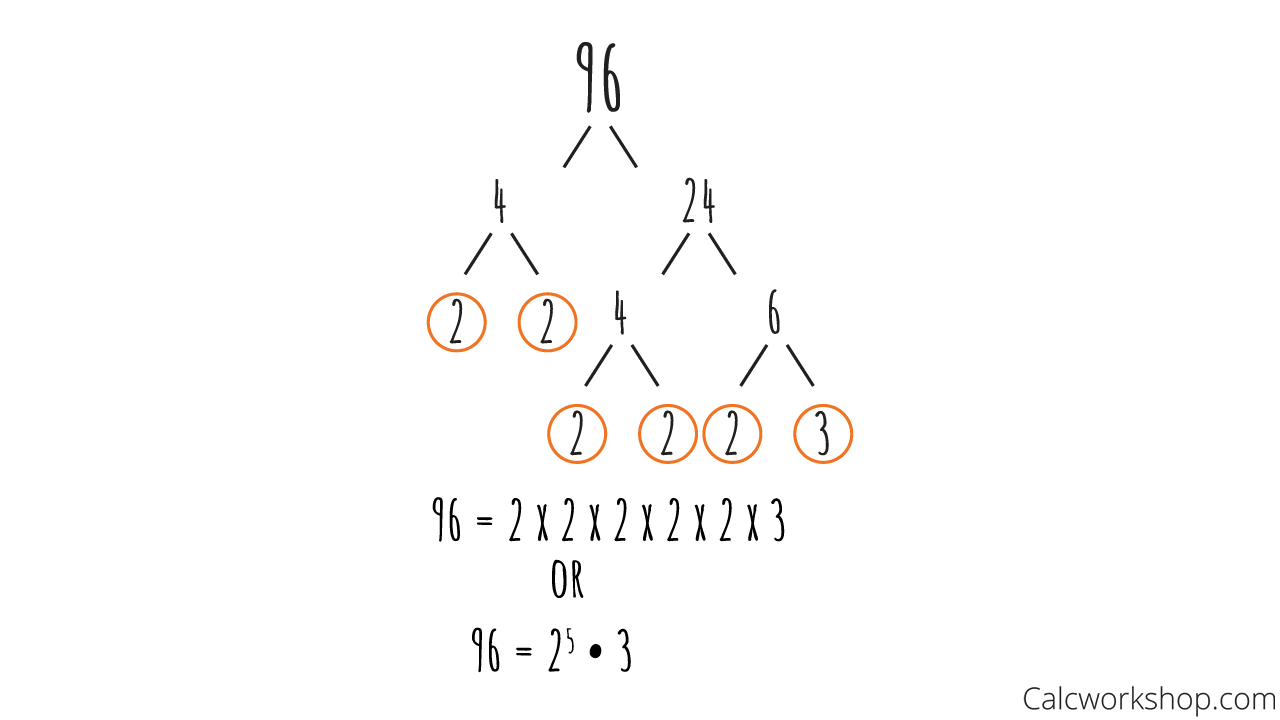
Prime Factorization Of 96
Now, seeing as the above example was an even number, it wasn’t too hard to find a factor to start our tree, but sometimes it’s not always obvious where to begin or whether the number is prime or composite.
Prime Number Algorithm (the shortcut)
Thankfully the prime number algorithm, sometimes called trial division, is a nice little trick to help us narrow down our search for factors (divisors).
The theorem states that if n is a composite integer, then n has a prime divisor less than or equal to the square root of n.

Prime Number Algorithm
Example
For this problem, suppose we are asked to find the prime factorization of 273.
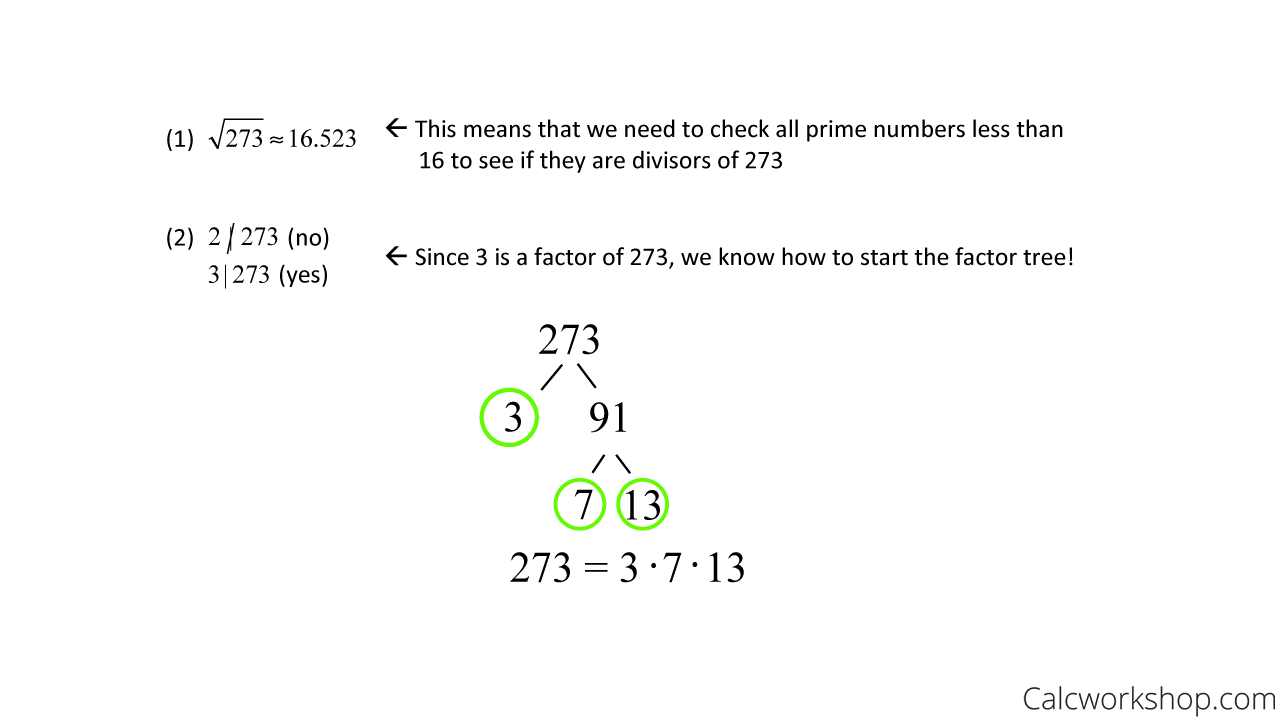
Trial Division — Example
Additionally, this trial division helps us to quickly find prime numbers as well, such as assume we are asked to find the prime factorization of 41.

Determine Primes Via Trial Division — Example
What Is Greatest Common Divisor
The greatest common divisor (GCD), also known as greatest common factor is the largest integer that divides evenly into each number in a given set. Formally, we define the (GCD) as follows:
Let a and b be integers. The largest integer d such at d|a and d|b is called the greatest common divisor of a and b, denoted gcd(a,b) as noted by Grand Valley State University.
How To Find Greatest Common Divisor (for a set of numbers)
- First, we write the prime factorization for each of the numbers in our set.
- Next, we choose the “fewest” common primes, as the GCD is the product of our fewest common primes.
Here’s a trick to keeping this straight. Remember that the GCD is nothing more than the GCF, or the greatest common factor. And that “F” stands for “fewest”!
Example
Sometimes it’s best to see this with an example. So, let’s find the gcd(12, 18).
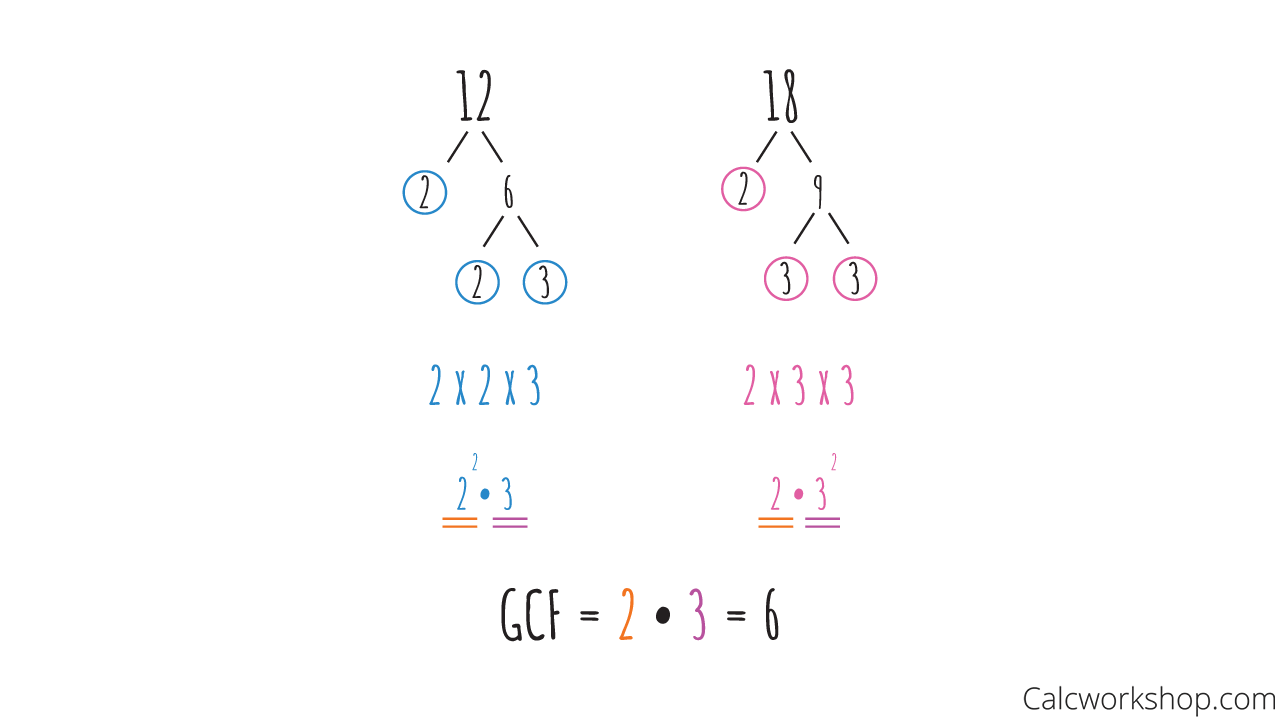
GCF of 12 and 18
In summary, all we did was create factor trees for our two integers to write our prime factorization. Then we found the “fewest” primes that they had in common, and that’s our GCD!

GCD Definition
Now, sometimes we will be given a set of numbers, where the greatest integer they have in common is 1. Whenever this happens, we say the set is relatively prime.
Example
For example, the gcd(13, 25) = 1 as the greatest integer that 13 and 25 have in common is 1. Therefore they are relatively prime.
Least Common Multiple
Similarly, the least common multiple (LCM) is the smallest positive integer divisible by two or more numbers.
And just like the GCD, we find the LCM by listing the prime factorization of each number. But instead of choosing the fewest, we will select the “most” of every integer we find this time. Notice how LCM ends with an “M” to help remind us that we are looking for the most or “max!”

LCM Definition
Example
For example, let’s find the gcd(15,18,24) and the lcm(15,18,24)
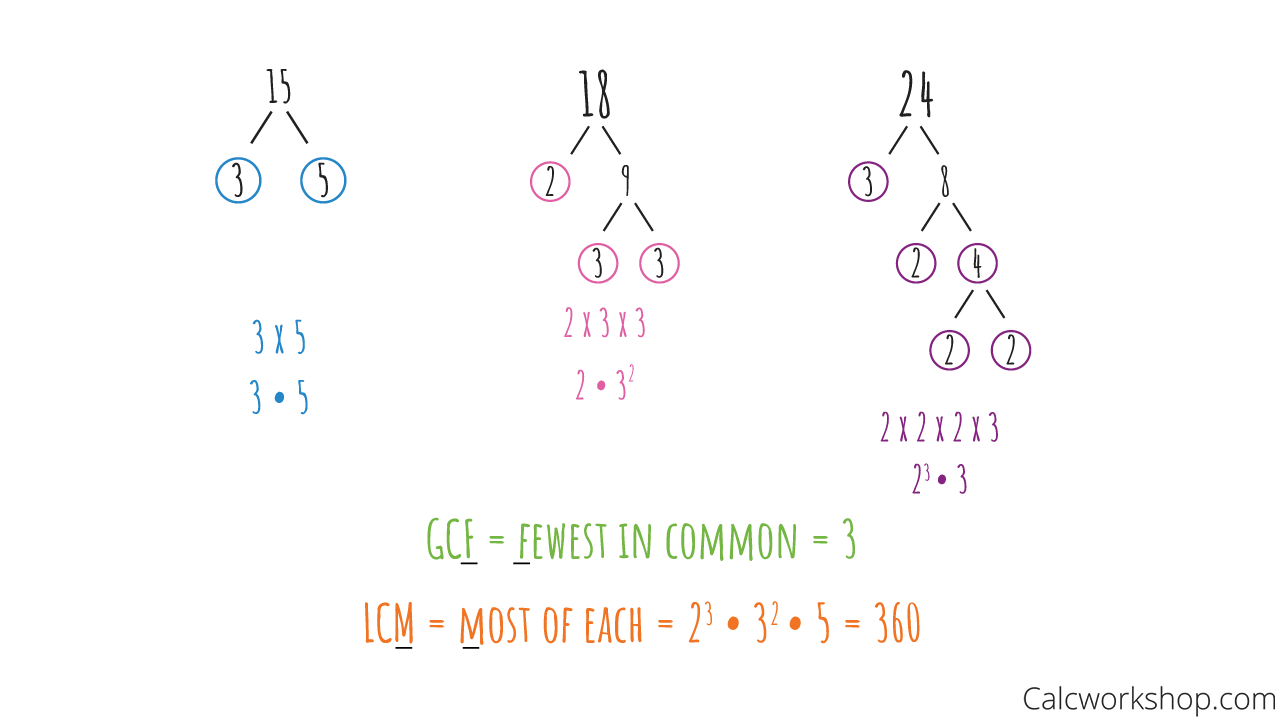
Find GCF and LCM of Three Numbers — Example
Euclidean Algorithm (the other method)
But did you know that there’s another way to find the GCD?
Yep, it’s called the Euclidean Algorithm, and it helps us find the greatest common divisor by utilizing our division algorithm!

Euclidean Algorithm Formula
Example
Let’s investigate how this works.
Okay, suppose we want to find the greatest common divisor of 1001 and 1331 using the Euclidean Algorithm.
- First, we list our two numbers, from largest to smallest, so we say gcd(1331,1001).
- Now we apply the division algorithm systematically until we find our greatest common factor.
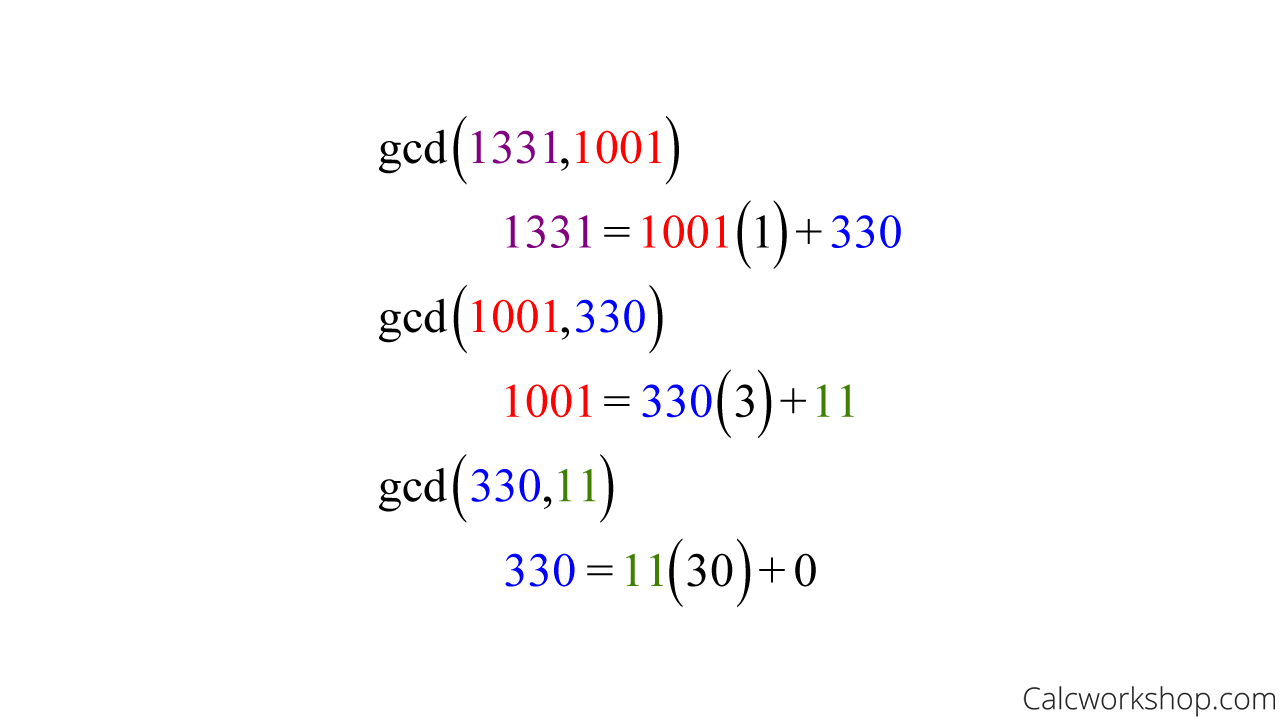
Euclidean Algorithm For GCD
And since the last nonnegative remainder is 11, gcd(1331,1001) = 11
Finding the GCD has never been easier!
Together we will review our techniques for finding primes, the greatest common divisor, least common multiplies, and how to quickly and effectively apply the Euclidean Algorithm to express the gcd for integers.
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples
59 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.