Did you know that Boolean Algebra helps us to understand probability theory, the geometry of sets, electrical circuits, and digital logic gates?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
But the most remarkable aspect of Boolean algebra is that it formalizes logical operations, the same way elementary algebra describes numerical operations, and it combines all our same rules from predicate logic!
This means that a predicate is a Boolean function whose values are either true or false, so everything we know from logic will help us understand Boolean algebra!
Okay, so Boolean algebra provides operations and rules for working with set {0,1} together with operators:
- Sum
- Product
- Complement
But here’s a big key, zero signifies false, and one denotes true!
In the following table, we lay out the Boolean operators side-by-side with its predicate logic counterparts. Notice the similarities, as this will guide you throughout this lesson.

Boolean Vs Predicate Logic
Boolean Algebra Symbols
Please note that some textbooks will use a period instead of a raised dot to symbolize Boolean products. For example, 1*1=1 is equivalent to saying 1.1=1.
Now, let’s use these Boolean operators to compute the following. We will do so using the Boolean operators as well as predicate logic:

Evaluate Using Boolean Operators
But we can extend our understanding beyond numbers to functions with variables.
A variable x is called a Boolean variable if it takes on values from B, where B = {0,1}, meaning x can either have the value of 0 or 1. And a Boolean function can be represented by a Boolean expression, constructed from Boolean variables and Boolean operations

Boolean Function Definition
The exponent, n, represents the number of Boolean variables. For example, F(x,y) is a degree 2 Boolean function because there are two variables, whereas F(w,x,y,z) is a degree 4 Boolean function.
All that this notation is saying is that we can apply algebraic operations to variables the same way we do with numbers, meaning we can combine boolean algebras using addition and multiplication. And our good friend, the truth table, is going to show us how in the following example!
Let Boolean variables, x, y, and z, and function f defined below.

Boolean Functions Of Degree 3 Table
But what’s so important to notice is that we’ve been doing this ever since learning about truth tables, as we can easily take our Boolean function and turn it into a truth table as seen below, yielding the same results!

Boolean Function Logic Table
This means that we already know how to show equivalence and verify functions, all thanks to truth tables, which is super cool!
Boolean Algebra Theorems
And the fun doesn’t stop there, as Boolean Algebra has similar identities to that of our equivalence laws from logic.

Boolean Algebra Identities Chart
This means that every Boolean algebra satisfies each of these laws and can be verified using a table or proof.
For example, let’s verify De Morgan’s law using a table and proof.
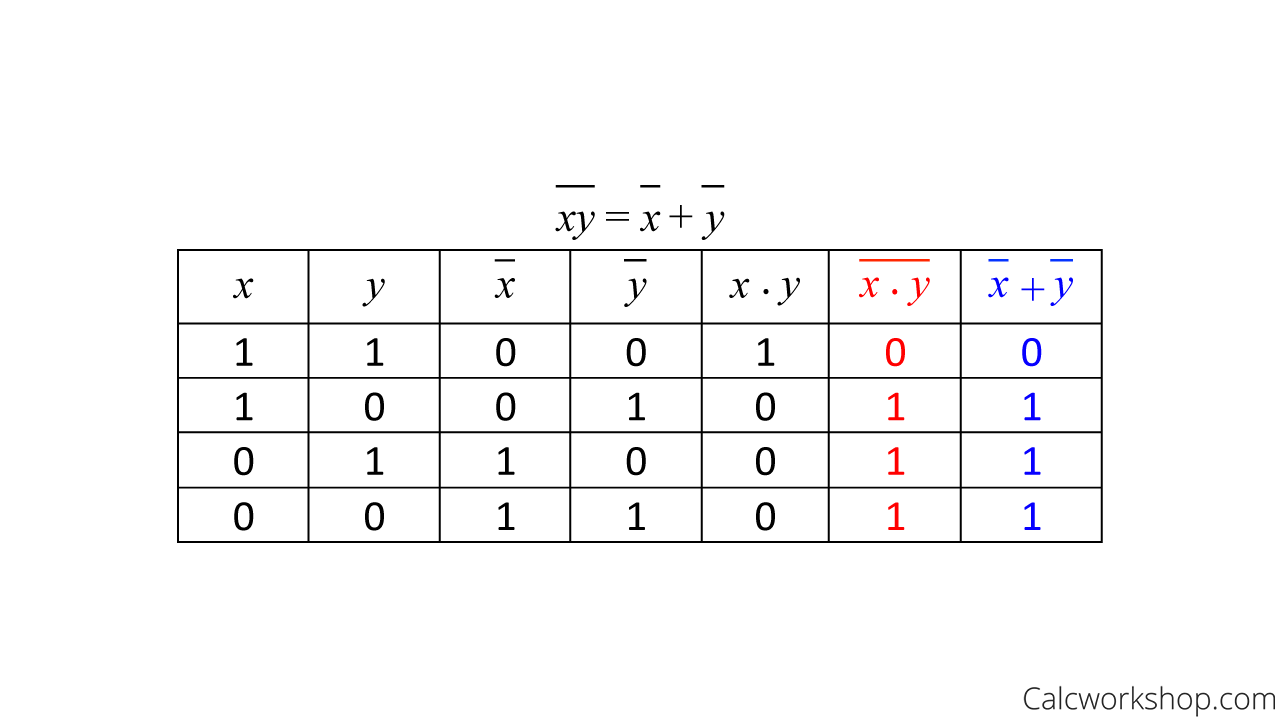
Demorgan’s Law Proof Truth Table
Now let’s prove De Morgan’s law with a proof, knowing that every element has a unique complement. In other words, we will need to show that the two propositions are complements to each other, namely A.A’ = 0.
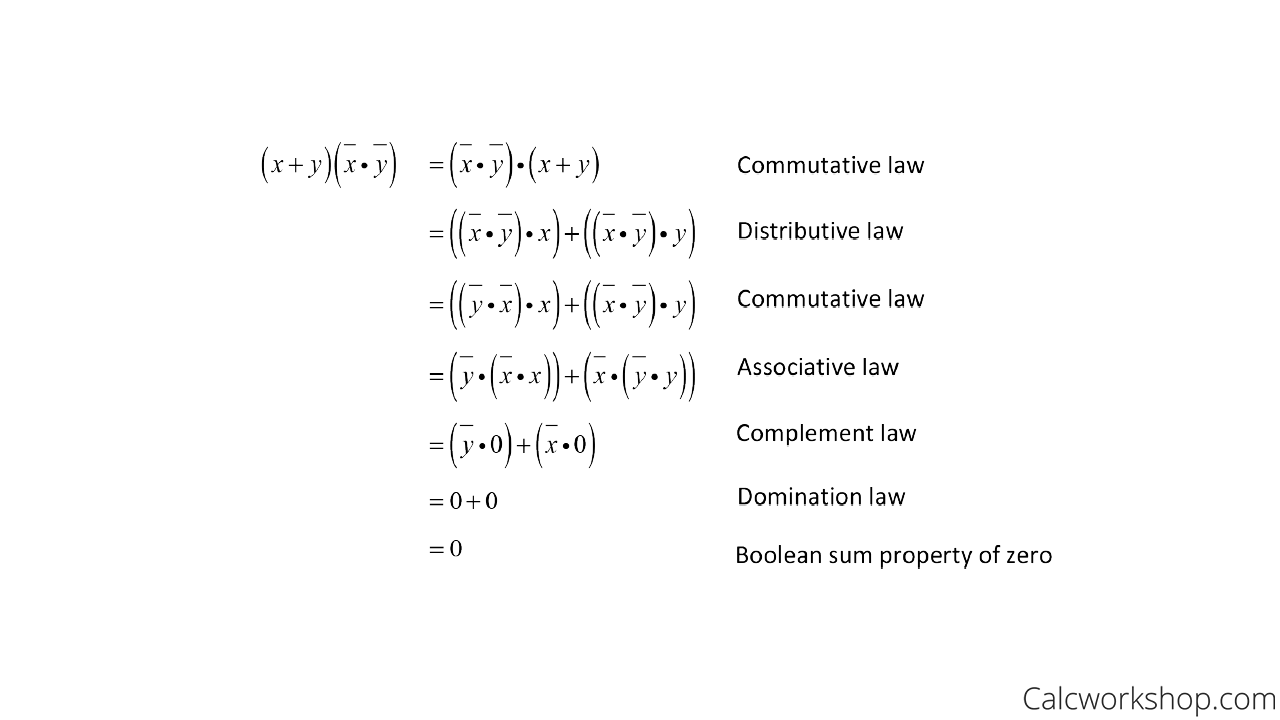
Proof Demorgan’s Law
Duality
What we can also observe from these proofs and identities is that Boolean algebras occur in pairs. And this leads us to the principle of duality.
The dual of a Boolean expression is found by interchanging each sum and product and by interchanging each 0 and 1, being careful to preserve the correct order of operation.
For example, let’s find the dual for the following expression.

Find Dual Expression
As you can see, Boolean Algebras is just as powerful as predicate logic and can be used in vastly many disciplines and industries. Together we will learn the rules and laws of Boolean algebra and functions and work through various examples, step-by-step.
Let’s jump right in!
also, University of Pennsylvania has handy PDF of boolean algebra laws.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 19 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.