How to set up a triple integral in spherical coordinates?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Interesting question, but why would we want to use spherical coordinates?
Easy, it’s when the object or region of study exhibits spherical symmetry, such as:
- Domes
- Globes & Balls
- Or Electrical & Gravitational Fields
Therefore, it makes sense that we would need to use a coordinate system that reflects such spherical symmetry.
Let’s take a closer look.
Spherical Coordinate System
Recall that the spherical coordinate system, sometimes referred to as the spherical polar coordinate system, describes a point in 3-space as \((\rho, \theta, \phi)\) where:
- \(\rho \) (rho) is the distance from the origin to the point such that \(\rho \ge 0\).
- \(\theta \) (theta) is the same angle in polar coordinates and is measured in radians representing the distance from the x-axis.
- And \(\phi \) (phi) is the angle between the positive z-axis and the line from the origin to the point and \(0 \le \phi \le \pi \).
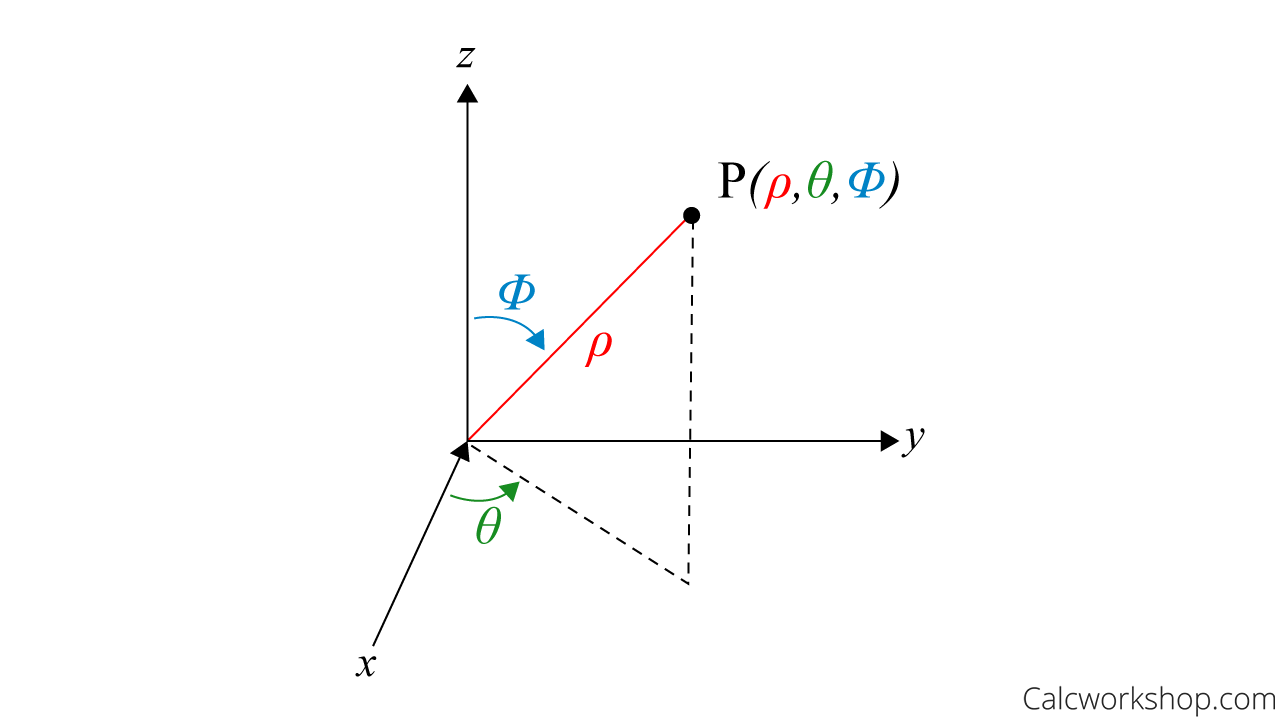
Spherical Coordinate System
Conversion Formulas
And here is a list of useful formulas that allow us to change to spherical coordinates from either rectangular or cylindrical systems.
\begin{equation}
\begin{array}{|c|c|c|}
\hline x=\rho \sin \phi \cos \theta & x^{2}+y^{2}+z^{2}=\rho^{2} & \rho \sin \phi=\sqrt{x^{2}+y^{2}} \\
y=\rho \sin \phi \sin \theta & \tan \theta=\frac{y}{x} & \tan \phi=\frac{\sqrt{x^{2}+y^{2}}}{z} \\
z=\rho \cos \phi & \theta=\theta & r=p \sin \phi \\
\hline
\end{array}
\end{equation}
Spherical Coordinates Triple Integral
The formula for triple integration in spherical coordinates is:
\begin{equation}
\iiint_{E} f(x, y, z) d V=\int_{c}^{d} \int_{\alpha}^{\beta} \int_{a}^{b} f(\rho, \theta, \phi) \rho^{2} \sin \phi d \rho d \theta d \phi
\end{equation}
Where E is a spherical wedge given by \(E = \left\{ {\left( {\rho ,\theta ,\phi } \right):a \le \rho \le b,\alpha \le \theta \le \beta ,c \le \phi \le d} \right\}\)
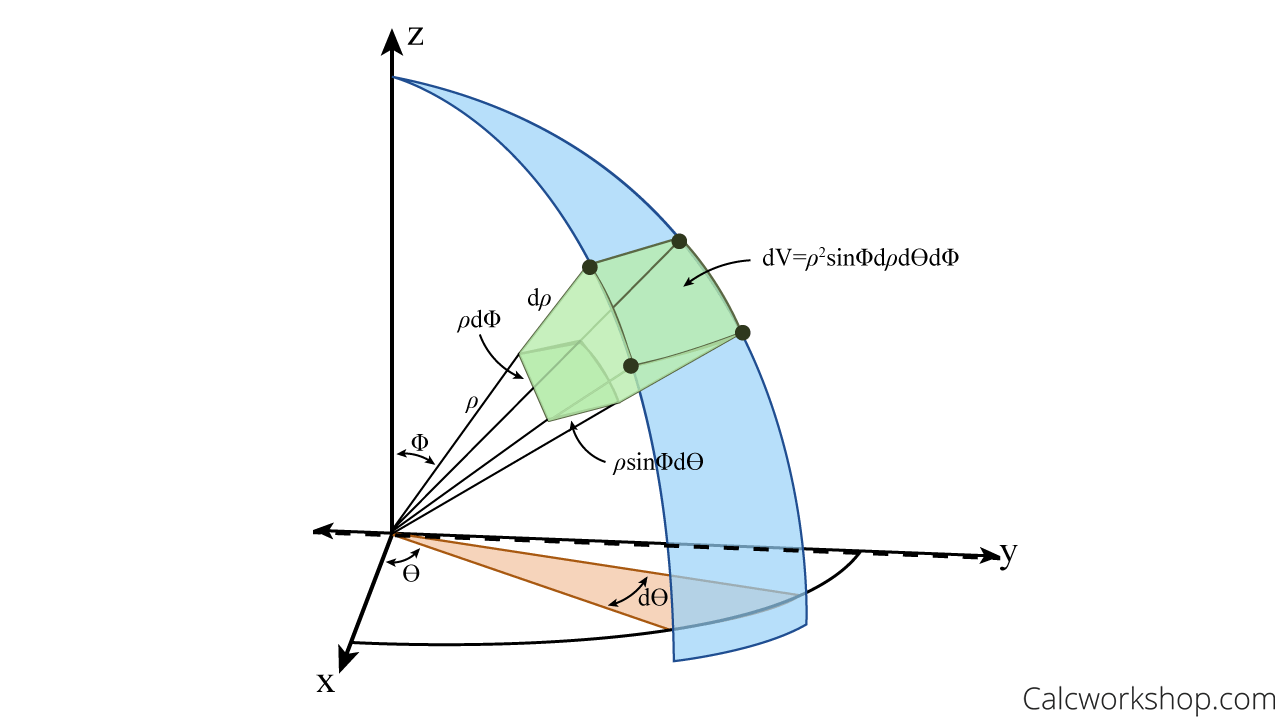
Volume Element In Spherical Coordinates
Please pay close attention to the Jacobian determinant of \({\rho ^2}\sin \phi \) as that enables us to transform from Cartesian coordinates to spherical coordinates.
And as we have come to expect with iterated integrals, we can change the order of \(d\rho \), \(d\theta \), and \(d\phi \) to allow for six forms or order of integration that we can utilize for spherical coordinates.
Example
Alright, so let’s look at an example.
Evaluate \(\iiint_{E} \frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}} d V\) where E is the unit ball: \(E = \left\{ {\left( {x,y,z} \right):{x^2} + {y^2} + {z^2} \le 1} \right\}\).
Okay, because the boundary E is a ball (sphere), we want to use spherical coordinates.
Thus, we need to change from rectangular to spherical using our formulas and find our limits of integration.
\begin{equation}
f(x, y, z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}} \rightarrow f(\rho, \theta, \phi)=\frac{1}{\sqrt{\rho^{2}}}=\frac{1}{\rho}, \rho^{2}=x^{2}+y^{2}+z^{2}
\end{equation}And since E is a unit ball we know that the distance from the center (origin) of the sphere is \(0 \le \rho \le 1\), with \({360^ \circ }\) rotation around the xy-plane such that \(0 \le \theta \le 2\pi \), and angle from the top of the ball (positive z-axis) to the bottom of the ball (negative z-axis) is \({180^ \circ }\)such that \(0 \le \phi \le \pi \).
So, the triple integral in spherical coordinates is:
\begin{equation}
\iiint_{E} \frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}} d V=\int_{0}^{\pi} \int_{0}^{2 \pi} \int_{0}^{1}\left(\frac{1}{\rho}\right) \rho^{2} \sin \phi d \rho d \theta d \phi=\int_{0}^{\pi} \int_{0}^{2 \pi} \int_{0}^{1}(\rho \sin \phi) d \rho d \theta d \phi
\end{equation}Now, we have to calculate the iterated triple integral by starting with our inner integral and integrating with respect to \(\rho \), rho.
\begin{equation}
\int_{0}^{\pi} \int_{0}^{2 \pi} \int_{0}^{1} \rho \sin \phi d \rho d \theta d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi} \int_{0}^{2 \pi}\left(\int_{0}^{1} \rho \sin \phi d \rho\right) d \theta d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi} \int_{0}^{2 \pi}\left(\left[\frac{\rho^{2} \sin \phi}{2}\right]_{0}^{1}\right) d \theta d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi} \int_{0}^{2 \pi}\left(\frac{\sin \phi}{2}\right) d \theta d \phi
\end{equation}Next, we will integrate with respect to \(\theta \), theta.
\begin{equation}
\int_{0}^{\pi} \int_{0}^{2 \pi} \frac{1}{2} \sin \phi d \theta d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi}\left(\int_{0}^{2 \pi} \frac{1}{2} \sin \phi d \theta\right) d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi}\left(\left[\frac{1}{2} \theta \sin \phi\right]_{0}^{2 \pi}\right) d \phi
\end{equation}\begin{equation}
=\int_{0}^{\pi}(\pi \sin \phi) d \phi
\end{equation}Lastly, we will integrate with respect to \(\phi \), phi.
\begin{equation}
\int_{0}^{\pi}(\pi \sin \phi) d \phi=-\left.\pi \cos \phi\right|_{0} ^{\pi}=2 \pi
\end{equation}
Excellent!
How To Find The Bounds Of A Triple Integral
Sometimes, it’s hard to determine which of the three coordinate systems to use when evaluating a triple integral. The key is to use whichever coordinate system that makes calculating the easiest!
Suppose you see the words “sphere” or “unit ball,” then you’re going to want to use spherical coordinates. But what about when it’s not so apparent?
Here’s a helpful guide you can use to choose the most appropriate coordinate system based on the region of integration:
- Cartesian \((x, y, z)\): Translation symmetry.
- Cylindrical \((r, \theta, z)\): Rotation symmetry in two-dimensions with translation symmetry in the third.
- Spherical \((\rho, \theta, \phi)\): Rotational symmetry in three-dimensions.
Together we will work through several examples of how to evaluate a triple integral in spherical coordinates and how to convert to spherical coordinates to find the volume of a solid.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.