What is a triple integral used for?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
To answer that question, we need to review what we know about the integrals we have learned along the way.
- A single integral represents the area under the curve above the x-axis and is the sum of an infinite number of rectangles over an interval in two-space.
- A double integral represents the volume under the surface above the xy-plane and is the sum of an infinite number of rectangular prisms over a bounded region in three-space.
- And a triple integral measures volume in four-space under a hypersurface above the xyz-hyperplane.
In other words, triple integrals are used to measure volume in 4D.
And before you start to panic, this is much easier than it appears.
While we can’t draw in four-space, we can draw in three-space, which is the domain for our hypersurface!
Moreover, triple integrals can also represent a volume of a 3D surface, just like a double integral can be used to describe the area or a 2D curve.
Phew!
Triple Integrals Defined
Let’s take a closer look at triple integrals and their properties.
Alright, so a triple integral is evaluated by three successive or iterated integrations, with six different possible orders of integration.
Let’s take a closer look
For instance, if a region \(R\) in \({\mathbb{R}^3}\) is defined by the inequalities \(a \le x \le b\), \(c \le y \le d\), and \(j \le z \le k\) and if \(f\left( {x,y,z} \right)\) is continuous on the region, then:
\begin{equation}
\iiint_{R} f(x, y, z) d V=\int_{a}^{b} \int_{c}^{d} \int_{j}^{k} f(x, y, z) d z d y d x
\end{equation}
\begin{equation}
\begin{aligned}
&=\int_{c}^{d} \int_{a}^{b} \int_{j}^{k} f(x, y, z) d z d x d y \\
&=\int_{a}^{b} \int_{j}^{k} \int_{c}^{d} f(x, y, z) d y d z d x \\
&=\int_{j}^{b} \int_{a}^{b} \int_{c}^{d} f(x, y, z) d y d x d z \\
&=\int_{c}^{d} \int_{j}^{k} \int_{a}^{b} f(x, y, z) d x d z d y \\
&=\int_{j}^{k} \int_{c}^{d} \int_{a}^{b} f(x, y, z) d x d y d z
\end{aligned}
\end{equation}
This means, thanks to Fubini’s theorem, we can use any of the six possible forms and obtain the same result.
Example
Let’s look at a problem to see this in action.
Evaluate \(\iiint_{D} 6 x^{3} y^{2} z d V\) over region \(D=\{(x, y, z): 0 \leq x \leq 2,0 \leq y \leq 3,-1 \leq z \leq 2\}\).
Well, seeing as our region \(D\) has all constant inequalities, we can choose any of the six forms to use to evaluate without having to worry about changing or fixing our bounds.
So, let’s randomly select \(dzdydx\) to calculate the iterated triple integral, such that we will integrate with respect to z first, then with respect to y, and lastly with respect to x.
\begin{equation}
\begin{gathered}
\int_{0}^{2} \int_{0}^{3} \int_{-1}^{2}\left(6 x^{3} y^{2} z\right) d z d y d x=\int_{0}^{2} \int_{0}^{3}\left(\int_{-1}^{2}\left(6 x^{3} y^{2} z\right) d z\right) d y d x \\
=\int_{0}^{2} \int_{0}^{3}\left(\left[3 x^{3} y^{2} z^{2}\right]_{-1}^{2}\right) d y d x \\
=\int_{0}^{2}\left(\int_{0}^{3}\left(9 x^{3} y^{2}\right) d y\right) d x \\
=\int_{0}^{2}\left(\left[3 x^{3} y^{3}\right]_{0}^{3}\right) d x \\
=\int_{0}^{2}\left(81 x^{3}\right) d x \\
=\left(\frac{81}{4} x^{4}\right]_{0}^{2} \\
=324
\end{gathered}
\end{equation}And the other five forms will give us the same result.
Seems easy enough, right?
Triple Integration Boundaries
But as we learned from double integrals over non-rectangular regions, the most challenging part of triple integration over general regions is determining the limits (bounds) for each integral.
Thankfully there are some helpful guidelines that help us to keep things straight and aid us on our quest for finding the limits of integration:
- Inner integral contains at most two variables.
- Middle integral contains at most one variable.
- Outer integral contains only constant values.
Example
So, let’s practice setting up or writing an iterated triple integral using our rules above.
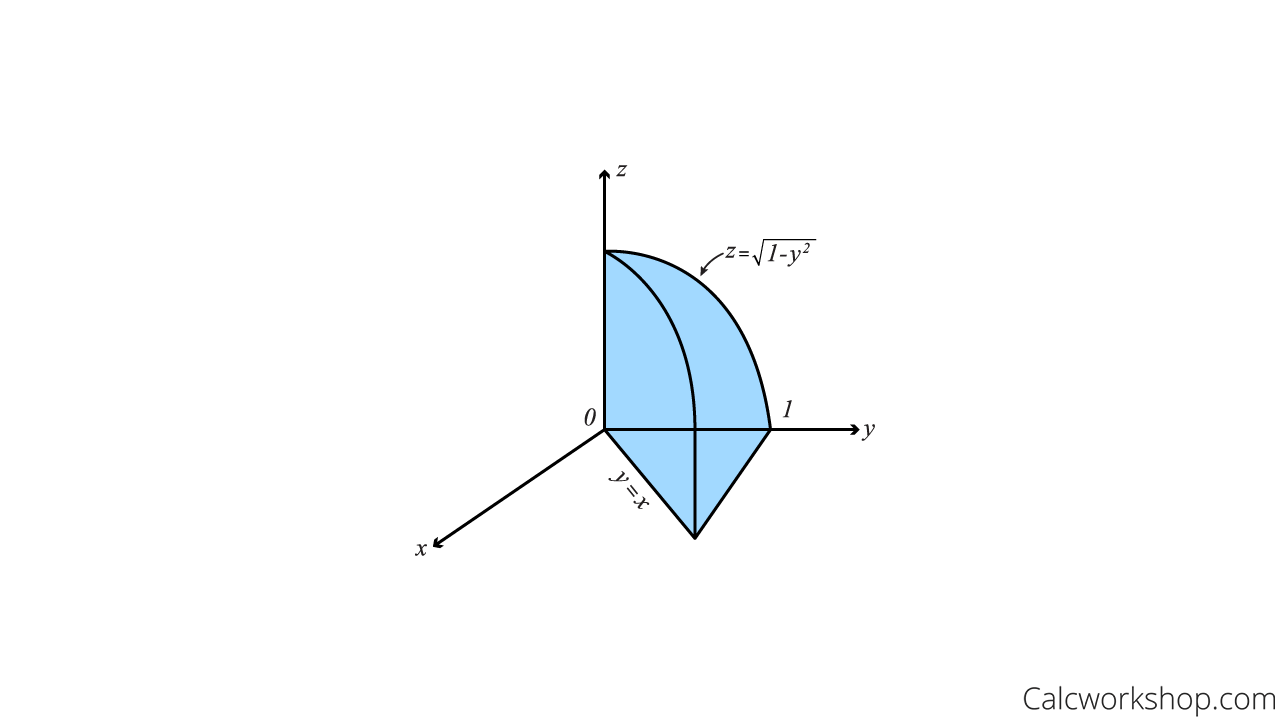
Evaluate \(\iiint_{D}(z) d V\) if \(D\) is the wedge in the first octant that is cut from the cylindrical function \({y^2} + {z^2} \le 1\) by the planes \(y = x\) and \(x = 0\).
Alright, so it is always helpful to sketch our surface using our constraints, when possible, as this will help us immensely in finding our bounds.
Surface Wedge First Octant
What do we notice?
The cylinder forms the upper surface of the solid, and the xy-plane forms the lower surface of the solid. And since the first octant bounds the wedge, this means that \(x \ge 0,\;y \ge 0,\;and\;z \ge 0\).
This means that if \({y^2} + {z^2} \le 1\)and \(z \ge 0\), then z varies from 0 to \(z = \sqrt {1 – {y^2}} \). And if \(y = x\) and \(x = 0\), then \(z\) varies from 0 to \(y\), denoted \(0 \le x \le y\). Furthermore, if \(z \ge 0\) and \({y^2} + {z^2} \le 1\) then \({y^2} + {\left( 0 \right)^2} = 1\) and tells us that \(y\) varies from 0 to 1.
So, our three bounds are:
\begin{equation}
0 \leq z \leq \sqrt{1-y^{2}} \quad, \quad 0 \leq x \leq y \quad, \quad 0 \leq y \leq 1
\end{equation}Now it’s time to set up our triple integral, remembering that our inner integral has up to two variables, the middle integral has up to one variable, and our outer integral has no variables.
Therefore, we must calculate as follows.
\begin{equation}
\int_{0}^{1} \int_{0}^{y} \int_{0}^{\sqrt{1-y^{2}}}(z) d z d x d y=\int_{0}^{1} \int_{0}^{y}\left(\int_{0}^{\sqrt{1-y^{2}}}(z) d z\right) d x d y
\end{equation}\begin{equation}
\begin{gathered}
=\int_{0}^{1} \int_{0}^{y}\left(\left[\frac{z^{2}}{2}\right]_{0}^{\sqrt{1-y^{2}}}\right) d x d y \\
\left.=\int_{0}^{1} \int_{0}^{y} \int_{0}^{y}\left(\frac{1}{2}\left(1-y^{2}\right)\right) d x\right) d y \\
=\int_{0}^{1}\left(\left[\frac{1}{2} x\left(1-y^{2}\right)\right]_{0}^{y}\right) d y \\
=\int_{0}^{1}\left(\frac{1}{2}\left(y-y^{3}\right)\right) d y \\
=\left(\frac{1}{2}\left(\frac{y^{2}}{2}-\frac{y^{4}}{4}\right)\right]_{0}^{1} \\
=\frac{1}{8}
\end{gathered}
\end{equation}
Excellent.
Together in our lesson, we will walk through several examples in detail to ensure that we can evaluate an iterated triple integral to find the volume of a solid. And we will devote our energy to learning how to identify our limits of integration, as they can be prickly at times.
But don’t worry. I’ll walk you through the steps, showing you some tricks along the way.
So, let’s dive right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.