It must be human nature to go for the simplest and least complicated approach to any task.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Sometimes the work necessary to simplify and calculate a double integral in Cartesian coordinates can be downright painful.
Consequently, we seek a more manageable approach for solving these problems.
Introducing…
Double Integrals In Polar Coordinates
Let’s start with
- A few reminders.
- A vital theorem.
- And some helpful observations.
Polar Coordinates Review
Having studied polar coordinates in precalculus and single-variable calculus, we know in this coordinate system, a point in the plane is determined by its distance (radius) from the origin (pole), and the angle theta, in radians, between the line from the origin to the point and the x-axis (polar axis).
And we can transform from Cartesian to polar and vice versa with the following formulas:
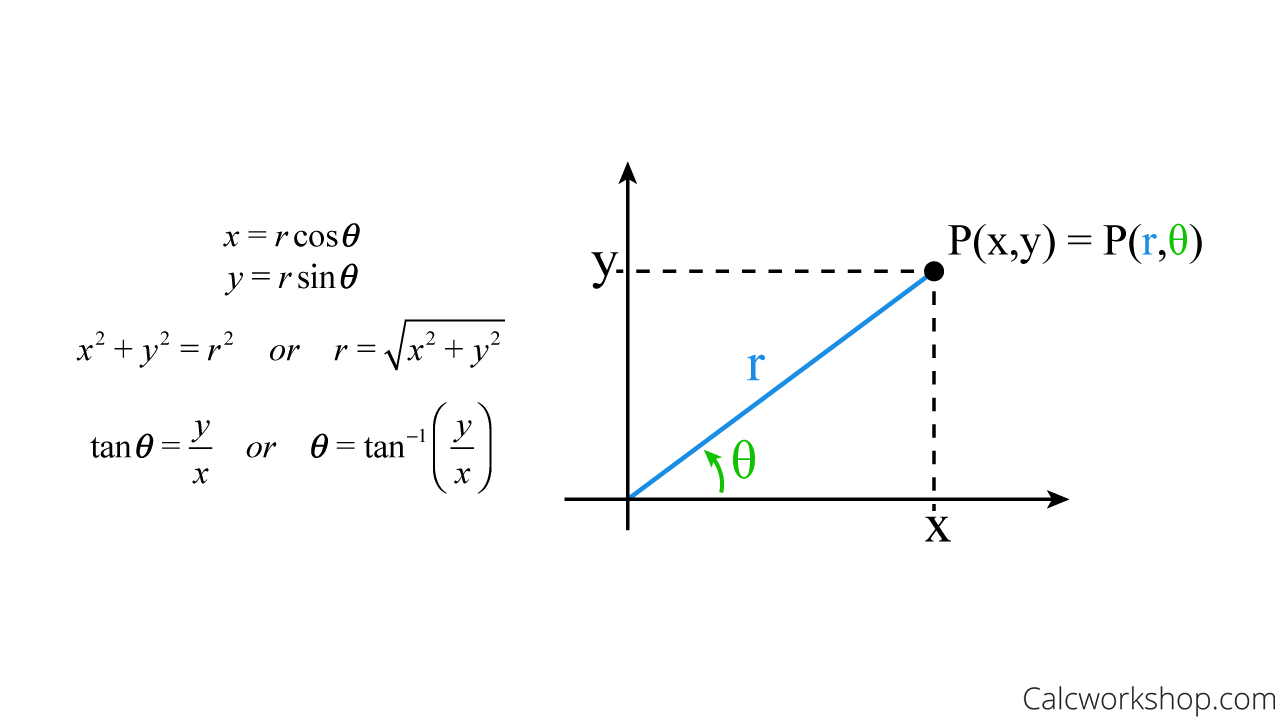
Polar Coordinates Formula
Now, we define the double integral for a continuous function in rectangular coordinates over the region \(R\) in the xy-plane by dividing subrectangles with sides parallel to the coordinate axes, as seen below in the image on the left.
But in polar coordinates, we will work with polar rectangles (triangular wedges), as seen below in the image on the right, where our region \(R\) is described as:
\begin{equation}
R=\left\{(r, \theta): r_{0} \leq r \leq r_{1}, \alpha \leq \theta \leq \beta\right\}
\end{equation}

Polar Rectangles Triangle Wedge
This means we can now express the double integral of function \(f\) in the region in polar coordinates as follows:
\begin{equation}
\iint_{R} f(x, y) d A=\int_{\alpha}^{\beta} \int_{r_{0}}^{r_{1}} f(r, \theta) r d r d \theta
\end{equation}
Consequently, rectangular sections in Cartesian coordinates are equivalent to disk sections in polar coordinates.
And the boundaries of each domain, whether it be a rectangle in Cartesian or a disk in polar, are defined by constant values of a coordinate.
Jacobian Transformation
But how can we change from rectangles to wedges? There has to be a catch!
And you would be right.
Did you notice an extra \(r\) on the right-hand side of our double integral in polar coordinates?
This is not a typo but a critical factor called the Jacobian transformation, enabling us to change from rectangular coordinates to polar coordinates for our iterated integrals.
And according to Paul’s Online Notes, the Jacobian transformation is invaluable for changing variables in a double integral.
Don’t worry.
In our video lesson, we will dive into the nuances of the Jacobian transformation or Jacobian determinant of first-order partial derivatives, and later again in a future class when we explore change of variables. Still, for now, you know that it is necessary and that whenever we integrate in polar, don’t forget the extra \(r\) to get \(rdrd\theta \).
Okay, so let’s demonstrate the awesomeness of polar coordinates for double integrals.
Example – Rectangular Vs Polar Coordinates
Evaluate The Double Integral In Rectangular Coordinates
\begin{equation}
\int_{0}^{1} \int_{x}^{\sqrt{2-x^{2}}}\left(x^{2}+y^{2}\right) d y d x
\end{equation}
Okay, this seems easy enough. We begin with the inner integral and integrate with respect to \(y\) while keeping \(x\) fixed.
\begin{equation}
\int_{0}^{1}\left(\int_{x}^{\sqrt{2-x^{2}}}\left(x^{2}+y^{2}\right) d y\right) d x
\end{equation}
\begin{equation}
=\int_{0}^{1}\left(\left(x^{2} y+\frac{1}{3} y^{3}\right]_{x}^{\sqrt{2-x^{2}}}\right) d x
\end{equation}
\begin{equation}
=\int_{0}^{1}\left(x^{2} \sqrt{2-x^{2}}+\frac{1}{3}\left(2-x^{2}\right)^{3 / 2}-\frac{4}{3} x^{3}\right) d x
\end{equation}
Now all we have to do is integrate this guy with respect to x:
\begin{equation}
=\int_{0}^{1}\left(x^{2} \sqrt{2-x^{2}}+\frac{1}{3}\left(2-x^{2}\right)^{3 / 2}-\frac{4}{3} x^{3}\right) d x
\end{equation}
Yikes!
This integral is rather tricky to compute by hand.
Ugh. I don’t even want to try…do you?
Nope. Because there’s an easier way, thanks to polar coordinates!
Evaluate The Iterated Integral By Converting To Polar Coordinates
So, rather than continuing down a painful trail in rectangular coordinates, we’re going to back up and transform the iterated integral into polar coordinates instead.
\begin{equation}
\int_{0}^{1} \int_{x}^{\sqrt{2-x^{2}}}\left(x^{2}+y^{2}\right) d y d x
\end{equation}
First, let’s focus on the region \(R\), which happens to be a portion of a circle (sector) upon closer inspection of the limits on the integrals.
\begin{equation}
\int_{0}^{1} \int_{x}^{\sqrt{2-x^{2}}}\left(x^{2}+y^{2}\right) d y d x
\end{equation}

Cartesian Coordinates To Polar With Constraints
Next, we can rewrite our constraints in polar coordinates.
\begin{gathered}
y=x \\
r \cos \theta=r \sin \theta \\
\cos \theta=\sin \theta \\
\frac{\sin \theta}{\cos \theta}=1 \\
\tan \theta=1 \\
\theta=\tan ^{-1}(1)=\frac{\pi}{4}
\end{gathered}
\end{equation}
\begin{gathered}
y=\sqrt{2-x^{2}} \\
y^{2}=2-x^{2} \\
x^{2}+y^{2}=2 \\
r^{2}=2 \\
r=\sqrt{2}
\end{gathered}
\end{equation}
\begin{gathered}
x=0 \\
r \cos \theta=0 \\
r=0 \quad \text { or } \quad \cos \theta=0 \\
r=0 \quad \theta=\cos ^{-1}(0)=\frac{\pi}{2}
\end{gathered}
\end{equation}
Alright, we have our new limit of integration in polar form.
\begin{equation}
0 \leq r \leq \sqrt{2} \text { and } \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}
\end{equation}
Now it’s time to rewrite our integrand in polar coordinates.
\begin{equation}
\begin{gathered}
f(x, y)=x^{2}+y^{2} \\
\downarrow \\
f(r, \theta)=r^{2}
\end{gathered}
\end{equation}
Finally, we are ready to drop everything into our double integral for polar formula.
\begin{equation}
\begin{aligned}
&\iint_{R} f(r, \theta) r d r d \theta \\
&\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \int_{0}^{\sqrt{2}}\left(r^{2}\right) r d r d \theta=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \int_{0}^{\sqrt{2}} r^{3} d r d \theta
\end{aligned}
\end{equation}
Wow!
Look how much easier this new and improved integral is to evaluate!
So, let’s go for it.
\begin{equation}
\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \int_{0}^{\sqrt{2}} r^{3} d r d \theta=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\left(\int_{0}^{\sqrt{2}} r^{3} d r\right) d \theta=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\left(\left[\frac{1}{4} r^{4}\right]_{0}^{\sqrt{2}}\right) d \theta=\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(1) d \theta=\left.\theta\right|_{\pi / 4} ^{\pi / 2}=\frac{\pi}{4}
\end{equation}
Nice!
Okay, so I think we’ve just proven that some problems are easier in polar coordinates, like the one above.
And here’s a helpful hint…
…Whenever we are given a region bounded by a circle, ring, or a portion of a circle or ring, we will want to convert to polar coordinates to make integration easier.
Together in our lesson, we will walk through numerous examples using our integration skills, such as u-substitution and half-angle identities, to evaluate double integrals in polar coordinates.
We will determine how to find regions bounded by two polar curves and discover how to change from a cartesian integral into a polar integral with ease.
There’s a lot to investigate, so let’s jump right into our lesson!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.