What’s the average?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
I guess it would depend on what you’re asking about.
- Average height?
- Average typing speed?
- Batting average?
- Central tendency of a data set?
- Etc.
Average Value – Integral
There are many types of “averages” but only one average value of a function.
Recall from single-variable calculus that the average value of \(f\) on the interval [a,b] as:
\begin{equation}
f_{\text {ave }}=\frac{1}{b-a} \int_{a}^{b} f(x) d x
\end{equation}
And that average value, also known as the mean value theorem for integrals, tells us that the area under a curve over a closed interval is equal to the area of a rectangle with the same width.
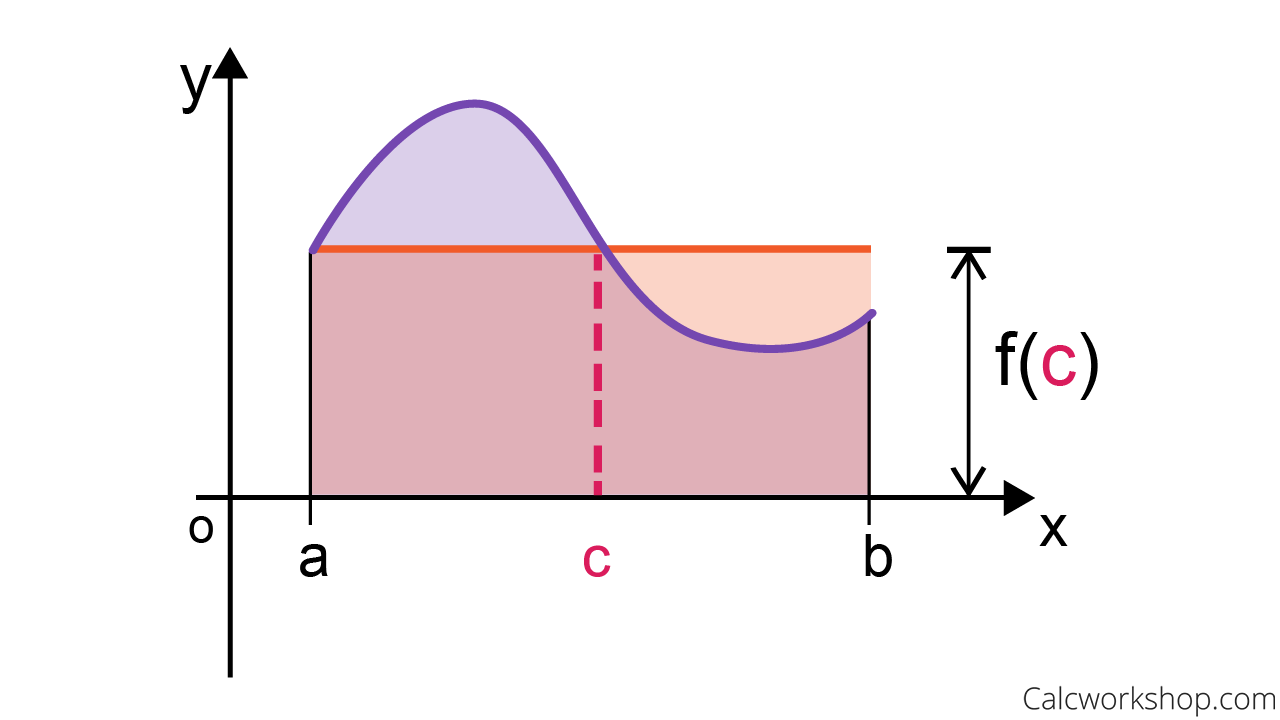
Mean Value Theorem for Integrals
Average Value Using Double Integrals
Well, guess what?
We can define the average value of a function of two variables in a similar fashion!
The average value of a function \(f\) of two variables defined on a rectangle \(R\) is:
\begin{equation}
f_{\text {ave }}=\frac{1}{A(R)} \iint_{R} f(x, y) d A, \text { where } A(R) \text { is the total area of } \mathrm{R}
\end{equation}
Which means for a function of two variables that the box with base \(R\) and height \({f_{ave}}\) has the same volume as the solid that lies under the graph of \(f\).
Cool!
Example
For instance, let’s estimate the average volume of the solid that lies below the surface:
\begin{equation}
z=f(x, y)=x^{2}+4 y
\end{equation}
And above the rectangle \(R = \left\{ {\left( {x,y} \right):0 \le x \le 2,0 \le y \le 3} \right\}\) with \(m = 2\) and \(n = 3\).
Use the midpoint rule to estimate the average volume.
First, we will sketch the subrectangles for the defined region \(R = \left[ {0,2} \right] \times \left[ {0,3} \right]\) and find\(A\left( R \right)\) and \(\Delta A\).
Subregion Rectangular Grid
\begin{equation}
\begin{aligned}
&A(R)=(2)(3)=6 \\
&\Delta A=d A=\Delta x \Delta y=\left(\frac{b-a}{m}\right)\left(\frac{d-c}{n}\right)=\left(\frac{2-0}{2}\right)\left(\frac{3-0}{3}\right)=1
\end{aligned}
\end{equation}Next, we will find our sample points, which are the points in the center of each rectangular region.
Sample Points Subregion
\begin{equation}
\left(\frac{1}{2}, \frac{1}{2}\right)\left(\frac{1}{2}, \frac{3}{2}\right)\left(\frac{1}{2}, \frac{5}{2}\right)\left(\frac{3}{2}, \frac{1}{2}\right)\left(\frac{3}{2}, \frac{3}{2}\right)\left(\frac{3}{2}, \frac{5}{2}\right)
\end{equation}Lastly, we substitute each point into our average value formula and simplify.
\begin{equation}
\begin{aligned}
&f_{\text {ave }}=\frac{1}{A(R)} \iint_{R} f(x, y) d A \\
&f_{\text {ave }}=\frac{1}{A(R)}\left[f\left(\frac{1}{2}, \frac{1}{2}\right) \Delta A+f\left(\frac{1}{2}, \frac{3}{2}\right) \Delta A+f\left(\frac{1}{2}, \frac{5}{2}\right) \Delta A+f\left(\frac{3}{2}, \frac{1}{2}\right) \Delta A+f\left(\frac{3}{2}, \frac{3}{2}\right) \Delta A+f\left(\frac{3}{2}, \frac{5}{2}\right) \Delta A\right] \\
&f_{\text {ave }}=\frac{1}{(6)}\left[\frac{9}{4}(1)+\frac{25}{4}(1)+\frac{41}{4}(1)+\frac{17}{4}(1)+\frac{33}{4}(1)+\frac{49}{4}(1)\right] \\
&f_{\text {ave }}=\frac{29}{4}
\end{aligned}
\end{equation}
Easy!
Double Integral Properties
But there’s more!
Take a look at the following properties of double integrals and see how they relate to our previous knowledge of integration from calculus 1.
- If \(f(x, y) \geq g(x, y)\) for all \((x, y)\) in \(\mathrm{R}\), then \(\iint_{R} f(x, y) d A \geq \iint_{R} g(x, y) d A\).
- If \(f\) is a continuous function, and \(f(x, y) \geq 0\), then \(\iint_{R} f d A\) is the volume of the solid lying above the region \(R\) in the xy-plane and below the graph of \(f\).
Linearity Of The Integral
- \(\iint_{R} c f(x, y) d A=c \iint_{R} f(x, y) d A\), where \(c\) is a constant.
- \(\iint_{R}[f(x, y) \pm g(x, y)] d A=\iint_{R} f(x, y) d A \pm \iint_{R} g(x, y) d A\), where \(c\) is a constant.
Addition On Rectangles
- \(\iint_{R} f(x, y) d A=\iint_{R_{1}} f(x, y) d A+\iint_{R_{2}} f(x, y) d A\), where \(R_{1}\) and \(R_{2}\) overlap only on a line segment and comprise all of \(R\).

Addition Rectangles Region
Together we will work through several examples on how to calculate the average value for a function of several variables and how to use our properties to evaluate double integrals over a region, \(R\).
It’s going to be fun, so let’s dive right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

