Did you know that a double integral can help us find the mass, center of mass, and moments of inertia of a lamina with variable density?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
Recall that a lamina is a thin plate, and the mass of this plate is concentrated about one point, which creates equilibrium.
This point is called the center of mass, gravity, or the centroid.
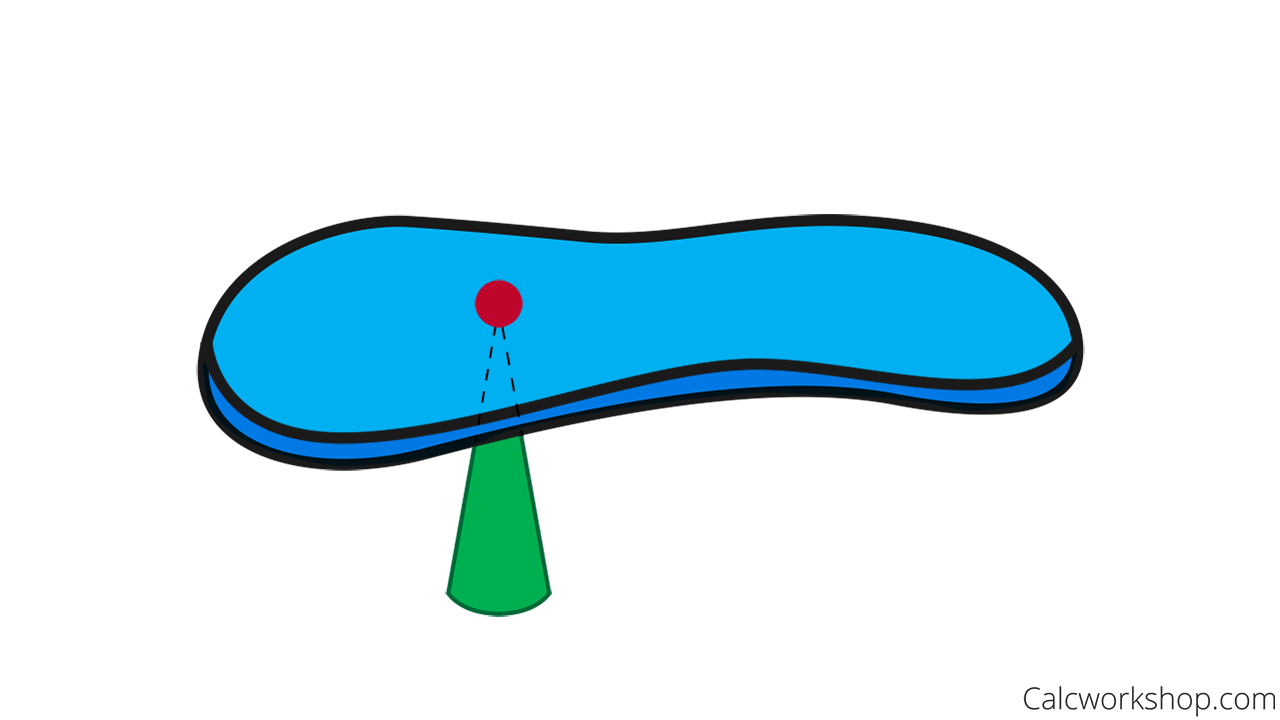
Centroid is the Point of Balance
And in single variable calculus, we were able to find moments and the center of mass of a lamina with constant or uniform density, but with the power of double integrals, we can now contemplate a lamina with variable density!
Let’s see how.
Mass
Okay, so a lamina’s mass-density measures its mass per unit area.
Suppose a thin plate occupies a region \(R\) in the xy-plane and its density at any point \(\left( {x,y} \right)\) in \(R\) is given by \(\rho \left( {x,y} \right)\), where \(\rho \) (pronounced rho) is a continuous function on \(R\).
Then the mass, \(m\), of the lamina is:
\begin{equation}
m=\lim _{k, l \rightarrow \infty} \sum_{i=1}^{k} \sum_{j=1}^{l} \rho\left(x_{i j}, y_{i j}\right) \Delta x \Delta y=\iint_{R} \rho(x, y) d A
\end{equation}
Therefore, if we consider a lamina with a density that varies across an object, the density at any point is proportional to the distance from the origin.
Example
Let’s walk through a problem.
Let \(R\) be the unit square \(R = \left[ {0,1} \right] \times \left[ {0,1} \right]\) and assume the density of \(R\) is given by the function \(\rho = \frac{1}{{1 + y}}\) so that \(R\) is denser near the x-axis.
Find the mass of \(R\).
All we have to do is drop our density function into our mass formula and calculate the double integral.
\begin{equation}
\begin{aligned}
&m=\iint_{R} \rho(x, y) d A \\
&m=\int_{0}^{1} \int_{0}^{1}\left(\frac{1}{1+y}\right) d y d x=\int_{0}^{1}\left((\ln (1+y)]_{0}^{1}\right) d x=\int_{0}^{1}(\ln 2) d x=\left.(\ln 2) x\right|_{0} ^{1}=\ln 2 \approx 0.693
\end{aligned}
\end{equation}
Not bad, right?
Center of Mass
Okay, so now that we know how to find the mass of a region, let’s focus on finding moments and the center of mass for variable density.
Mass Moments
If \(\rho \) is a continuous density function on the lamina corresponding to a plane region \(R\), then the moments of mass are as follows:
\begin{equation}
\begin{array}{|c|c|}
\hline \text { Moment of mass with respect to the x-axis } & \text { Moment of mass with respect to the y-axis } \\
\hline M_{x}=\iint_{R} y \rho(x, y) d A & M_{y}=\iint_{R} x \rho(x, y) d A \\
\hline
\end{array}
\end{equation}
Thus, the center of mass of \(R\) is \((\bar{x}, \bar{y})=\left(\frac{M_{y}}{m}, \frac{M_{x}}{m}\right)\), where \(m=\iint_{R} \rho(x, y) d A\).
Example
So, using our previous example, let’s now find the moments and center of mass of our unit square region \(R\).
Recall, \(R = \left[ {0,1} \right] \times \left[ {0,1} \right]\) with density function \(\rho = \frac{1}{{1 + y}}\).
So our first step is to find our moments with respect to x-axis and y-axis separately.
Again, all we have to do is drop our density function into our iterated integrals formulas.
\begin{equation}
M_{x}=\int_{0}^{1} \int_{0}^{1} y\left(\frac{1}{1+y}\right) d y d x=\int_{0}^{1} \underbrace{\left(\int_{0}^{1}\left(\frac{y}{1+y}\right) d y\right)}_{\text {apply Long Division }} d x
\end{equation}\begin{equation}
=\int_{0}^{1}\left(\int_{0}^{1}\left(1-\frac{1}{1+y}\right) d y\right) d x
\end{equation}\begin{equation}
=\int_{0}^{1}\left(y-\left.\ln (1+y)\right|_{0} ^{1}\right) d x
\end{equation}\begin{equation}
=\int_{0}^{1}(1-\ln 2) d x=1-\ln 2
\end{equation}\begin{equation}
M_{y}=\int_{0}^{1} \int_{0}^{1} x\left(\frac{1}{1+y}\right) d y d x=\int_{0}^{1}\left(\int_{0}^{1}\left(\frac{x}{1+y}\right) d y\right) d x
\end{equation}\begin{equation}
=\int_{0}^{1}\left(\left.x \ln (1+y)\right|_{0} ^{1}\right) d x
\end{equation}\begin{equation}
=\int_{0}^{1}(x \ln 2) d x
\end{equation}\begin{equation}
=\left.\frac{\ln 2}{2} x^{2}\right|_{0} ^{1}=\frac{\ln 2}{2}
\end{equation}Alright, now we are able to compute the center of mass, using our formula:
\begin{equation}
(\bar{x}, \bar{y})=\left(\frac{M_{y}}{m}, \frac{M_{x}}{m}\right)
\end{equation}Where \(m=\int_{0}^{1} \int_{0}^{1}\left(\frac{1}{1+y}\right) d y d x=\ln 2\) from our previous calculations.
\begin{equation}
(\bar{x}, \bar{y})=\left(\frac{\left(\frac{\ln 2}{2}\right)}{\ln 2}, \frac{(1-\ln 2)}{\ln 2}\right)=(0.5,0.442)
\end{equation}
See. It’s pretty straightforward.
Moments of Inertia
And with this knowledge, we will see how to find the second moment, or Moments of Inertia, about a line.
Recall from single-variable calculus that the moment of inertia of a particle of mass \(m\) about an axis is defined to be \(m{r^2}\), where \(r\) is the distance from the particle to the axis.
And when we extend this concept to a lamina with variable density \(\rho \left( {x,y} \right)\) the results are as follows:
\begin{equation}
\begin{array}{|c|c|c|}
\hline \begin{array}{c}
\text { Moment of Inertia about the } \\
\text { x-axis }
\end{array} & \begin{array}{c}
\text { Moment of Inertia about the } \\
\text { y-axis }
\end{array} & \begin{array}{c}
\text { Moment of Inertia about the } \\
\text { Origin }
\end{array} \\
\hline I_{x}=\iint_{R} y^{2} \rho(x, y) d A & I_{y}=\iint_{R} x^{2} \rho(x, y) d A & I_{0}=\iint_{R}\left(x^{2}+y^{2}\right) \rho(x, y) d A \\
\hline
\end{array}
\end{equation}
Please note that the moment of inertia about the origin is also called the polar moment of inertia:
\begin{equation}
I_{0}=I_{x}+I_{y}
\end{equation}
Additionally, it’s important to note that moment of inertia plays a similar role in rotational motion that mass plays in linear motion.
In other words, if mass is a measure of the tendency of matter to resist a change in straight line motion, then as UC Davis states, the moment of inertia is a measure of the tendency of matter to resist a change in rotational motion.
Cool!
Charge Density
But that’s not all a double integral can do for us.
For example, if an electric charge is distributed over a region \(R\) and the charge density is given by \(\sigma \left( {x,y} \right)\), measured in coulombs per square unit, at a point \(\left( {x,y} \right)\) in \(R\), then the total charge \(Q\) can be found by:
\begin{equation}
Q=\iint_{R} \sigma(x, y) d A
\end{equation}
This is the exact same equation for finding mass!
Probability Density
And that’s not all, because double integrals can help us to consider the probability density function too.
In particular, we will learn how to find the Probability Density Function and the joint probability of two random variables falling within a specific range.
Why?
Because there are many times when we are interested in two random variables and how they are related, such as temperature and pressure, or height and age.
Thus, if we have two random variables, \(X\) and \(Y\), then the pair \(\left( {x,y} \right)\) takes on the values in the plane.
And the probability per unit area of \(\left( {x,y} \right)\) landing within a certain region \(R\) is called the joint probability density function, denoted \({f_{X,Y}}\left( {x,y} \right)\) , and is found as
\begin{equation}
P(X, Y)=\iint_{R} f_{X, Y}(x, y) d A
\end{equation}
Hence, the probability of a random variable falling within a particular range of values is given by the iterated integral of the variable’s joint density function, which is the area under the density function between the lowest and greatest values for the range.
Don’t worry. We will work through an example together to help make sense of things. But please know that this is only a taste of double integrals and probability. You can read and view more in my Probability and Statistics course for additional in-depth analysis.
This video is action-packed with lots of applications of what the iterated double integral can accomplish.
Our goal is to dive into some applications of double integral and walk through numerous examples on finding mass, moments, center of mass, moments of inertia, and more.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.