Applications to Computer Graphics

In this video lesson, we will learn about Applications for Computer Graphics.

The mathematics behind computer graphics is closely connected with matrix multiplication and linear transformations. Cornell University explains that Computer Graphics is pretty much everything on computers that is not text or sound, such as geometric modeling, image rendering, animation, simulators for flight and driving, CAD programs, architectural visualization, and virtual reality.

Exploring Basic Mathematics and Transformations in Computer Graphics

For our lesson, we will focus on the more basic mathematics used in Computer Graphics to manipulate and display graphical images, and we will use our previous knowledge of transformations to help us.

Review of Transformations and an Example of Matrix Transformation

We begin our lesson by quickly reviewing our previously learned transformations, such as Contractions/Expansions, Shears, Reflections, Translation (moving an object horizontally or vertically), and Rotations.

For example, let’s compute the composite matrix transformation that performs a horizontal shear of 0.25 and then reflects through the \(\mathrm{x}\)-axis.

First, we will take apply the horizontal shear transformation, where \(k=0.25\)

\begin{align*}
\left[\begin{array}{ll}
1 & k \\
0 & 1
\end{array}\right] \mapsto\left[\begin{array}{cc}
1 & 0.25 \\
0 & 1
\end{array}\right]
\end{align*}

Then, we will complete the transformation by reflecting our matrix over the \(\mathrm{x}\)-axis, causing all the \(y\)-values to change signs, creating the final result of:

\begin{align*}
\left[\begin{array}{cc}
1 & 0.25 \\
0 & -1
\end{array}\right]
\end{align*}

The Transition from 2D to 3D: Introduction to Homogeneous Coordinates

But we don’t like it in a 2D world. What would happen if we wanted to make our transformations or graphics more realistic? In other words, how do we make things 3D?

We need Homogeneous Coordinates!

If each point \((x, y)\) in \(\mathbb{R}^{2}\) can be identified with the homogeneous coordinate \((x, y, 1)\) on the plane in \(\mathbb{R}^{3}\), thus allowing us to apply transformations for \(3 \times 3\) matrices. For example, any linear transformation on \(\mathbb{R}^{2}\) is presented with respect to homogeneous coordinates by a partitioned matrix of the form \(\left[\begin{array}{cc}A & 0 \\ 0 & 1\end{array}\right]\), where \(\mathrm{A}\) is a \(2 \times 2\) matrix then typical transformations are as follows:

Composite Transformations: The Magic of Computer Graphics

But the magic of computer graphics is the ability to put more than one transformation together. In other words, being able to create composite transformations, like translate, then rotate or reflect, then scale.

In this video, we will look at six examples and learn how to put our transformations together to create a fluid graphic by reversing the order of operations using what is known as composite matrix multiplication.

Reverse Order of Operations: The Secret Sauce of Composite Transformations

Wait! What’s this about reversing the order?

Yep! This is the secret sauce! We reverse the order of multiplication…the first transformation goes last, while the last transformation goes first.

The movement of a figure or image on a computer requires two or more transformations, called composite transformations. Then such transformations correspond to a matrix multiplication with homogeneous coordinates by reversing the order of multiplication!

An Example of Composite Transformation: Scaling, Rotation, and Translation

For example, let’s find the \(3 \times 3\) matrix that corresponds to the composite transformations of a scaling by 2, a rotation of \(60^{\circ}\), and finally, a translation that adds \((-3,4)\) to each point of the figure.

First, we are asked to scale by 2 so that the transformation looks like this:

\(\left[\begin{array}{lll}r & 0 & 0 \\ 0 & t & 0 \\ 0 & 0 & 1\end{array}\right] \Rightarrow\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1\end{array}\right]\)

Next, we are asked to rotate \(60^{\circ}\), and that transformation looks like this:

\begin{align*}
\left[\begin{array}{ccc}
\cos 60^{\circ} & -\sin 60^{\circ} & 0 \\
\sin 60^{\circ} & \cos 60^{\circ} & 0 \\
0 & 0 & 1
\end{array}\right] \Rightarrow\left[\begin{array}{ccc}
1 / 2 & -\sqrt{3} / 2 & 0 \\
\sqrt{3} / 2 & 1 / 2 & 0 \\
0 & 0 & 1
\end{array}\right]
\end{align*}

And thirdly, we want to translate each point by \((-3,4)\), which looks like this:

\begin{align*}
\left[\begin{array}{lll}
1 & 0 & h \\
0 & 1 & k \\
0 & 0 & 1
\end{array}\right] \Rightarrow\left[\begin{array}{ccc}
1 & 0 & -3 \\
0 & 1 & 4 \\
0 & 0 & 1
\end{array}\right]
\end{align*}

So, we combine all of these transformations for the composite transformation by reversing the order. In essence, we start with our third transformation (translation), then multiply it by our second transformation (rotation) and multiply this product by our first transformation \((\) scaling)

Cool!

Next Steps

In this lesson, you will:

• Look at new and exciting work in computer graphics connected to molecular modeling and experimental drug research
• Examine Homogeneous 3D Coordinates and Perspective Projections
• Learn the Perspective Matrix Equations
• Use it to find the image under a given perspective projection

Jump right in and start exploring!

Video Tutorial w/ Full Lesson & Detailed Examples

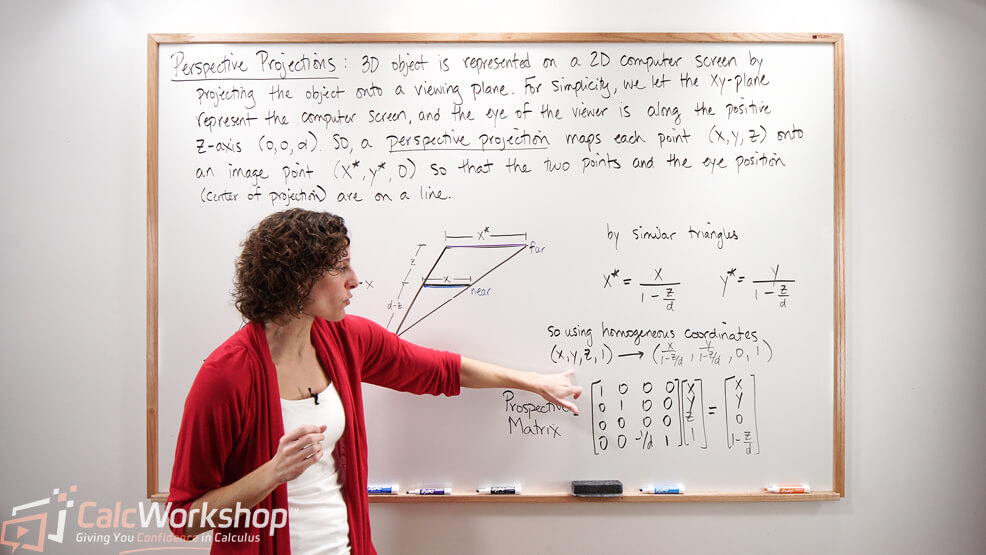
Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.