Have you heard of the rules of inference?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
They’re especially important in logical arguments and proofs, let’s find out why!
While the word “argument” may mean a disagreement between two or more people, in mathematical logic, an argument is a sequence or list of statements called premises or assumptions and returns a conclusion.
An argument is only valid when the conclusion, which is the final statement of the opinion, follows the truth of the discussion’s preceding assertions.
Consequently, it is our goal to determine the conclusion’s truth values based on the rules of inference.
Definition
The rules of inference (also known as inference rules) are a logical form or guide consisting of premises (or hypotheses) and draws a conclusion.
A valid argument is when the conclusion is true whenever all the beliefs are true, and an invalid argument is called a fallacy as noted by Monroe Community College.
In other words, an argument is valid when the conclusion logically follows from the truth values of all the premises.
There are two ways to form logical arguments, as seen in the image below. We will be utilizing both formats in this lesson to become familiar and comfortable with their framework.

Valid Argument — Definition
Basic Example
Now, before we jump into the inference rules, let’s look at a basic example to help us understand the notion of assumptions and conclusions.
Is this argument valid?

Logical Argument — Example
Without using our rules of logic, we can determine its truth value one of two ways.
- Surmising the fallacy of each premise, knowing that the conclusion is valid only when all the beliefs are valid.
- Construct a truth table and verify a tautology.
From the above example, if we know that both premises “If Marcus is a poet, then he is poor” and “Marcus is a poet” are both true, then the conclusion “Marcus is poor” must also be true.
And using a truth table validates our claim as well.
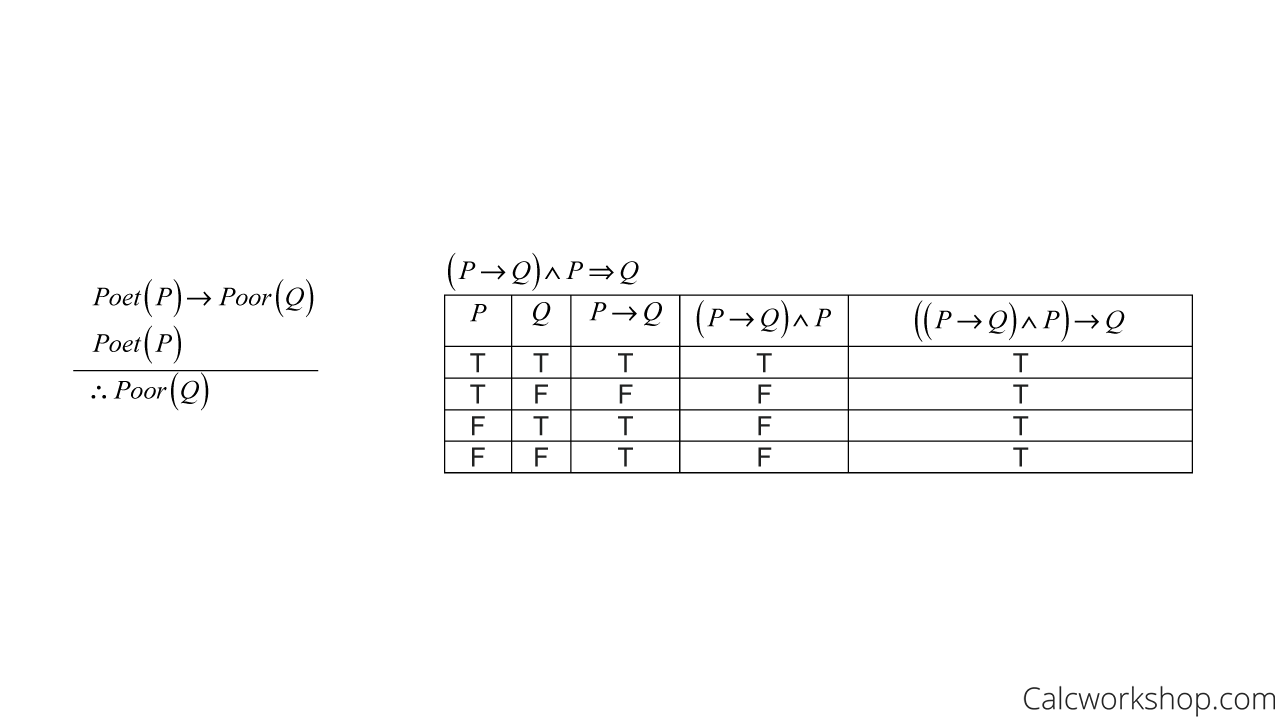
Valid Argument Truth Table
Rules Of Inference Examples
But what if there are multiple premises and constructing a truth table isn’t feasible?
Thankfully, we can follow the Inference Rules for Propositional Logic!
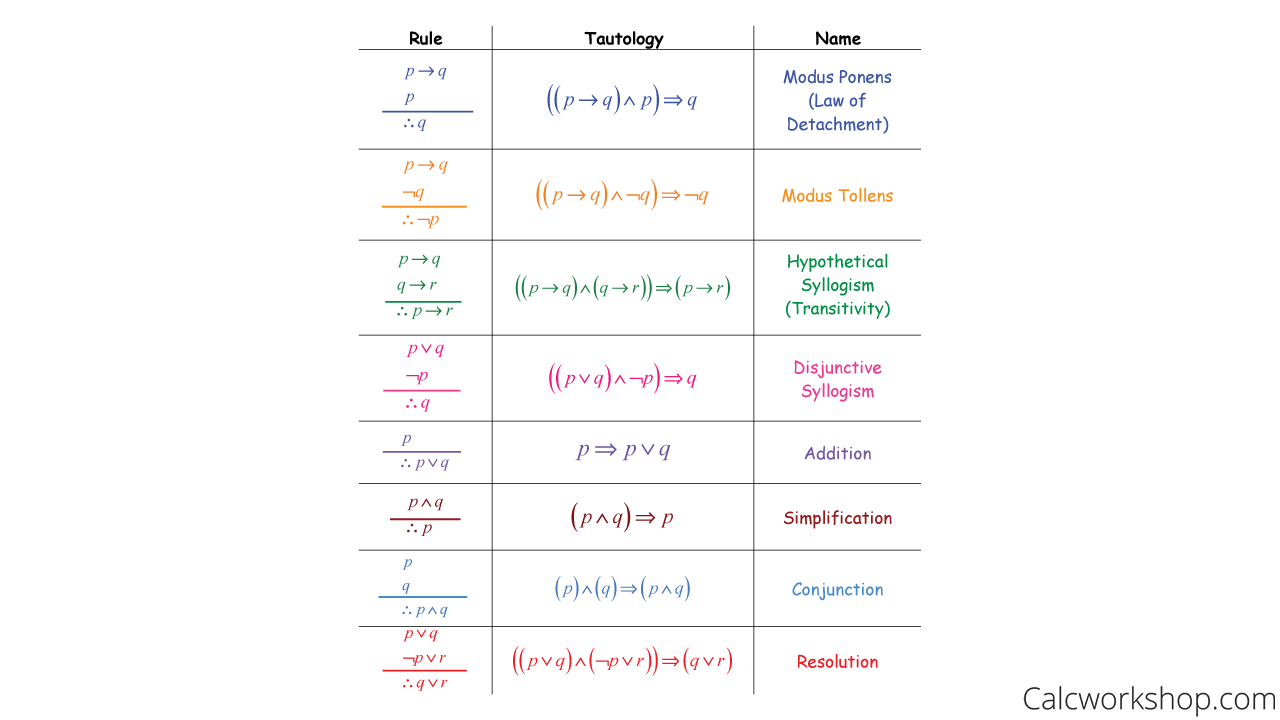
Rules Of Inference — Chart
Now, these rules may seem a little daunting at first, but the more we use them and see them in action, the easier it will become to remember and apply them.
Let’s look at an example for each of these rules to help us make sense of things.
Let p be “It is raining,” and q be “I will make tea,” and r be “I will read a book.”
Example — Modus Ponens
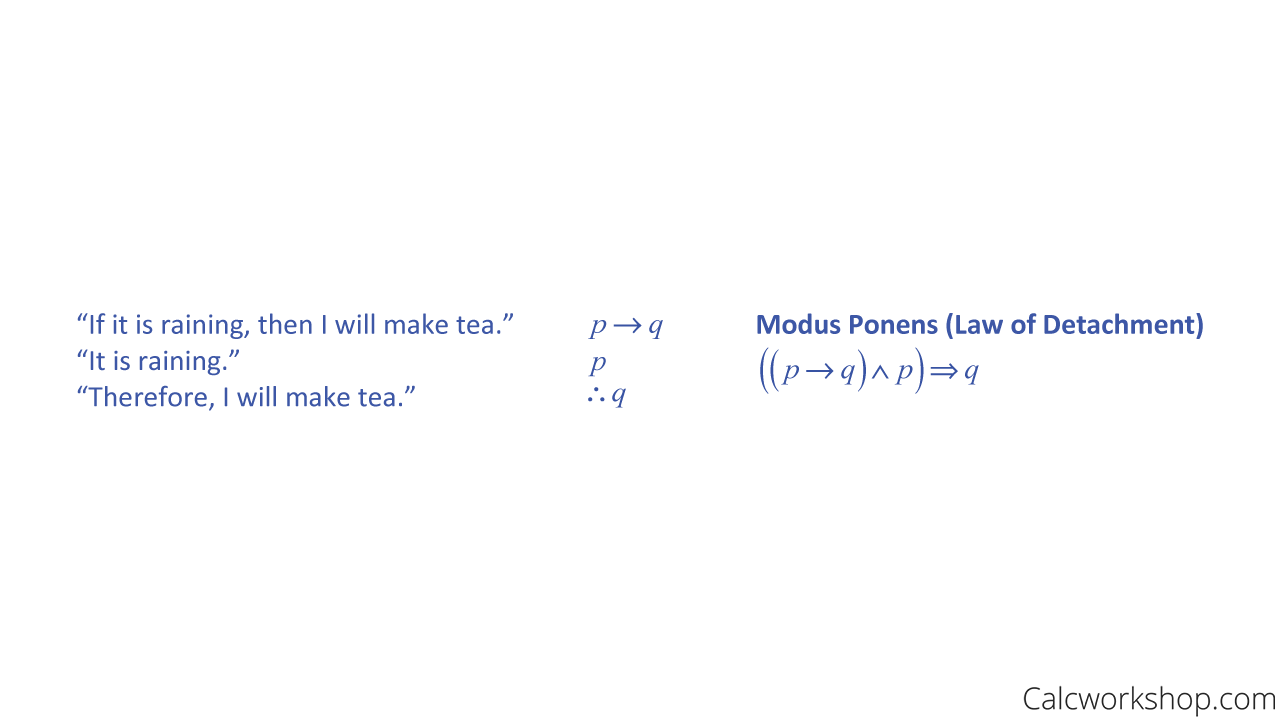
Modus Ponens — Example
Example — Modus Tollens
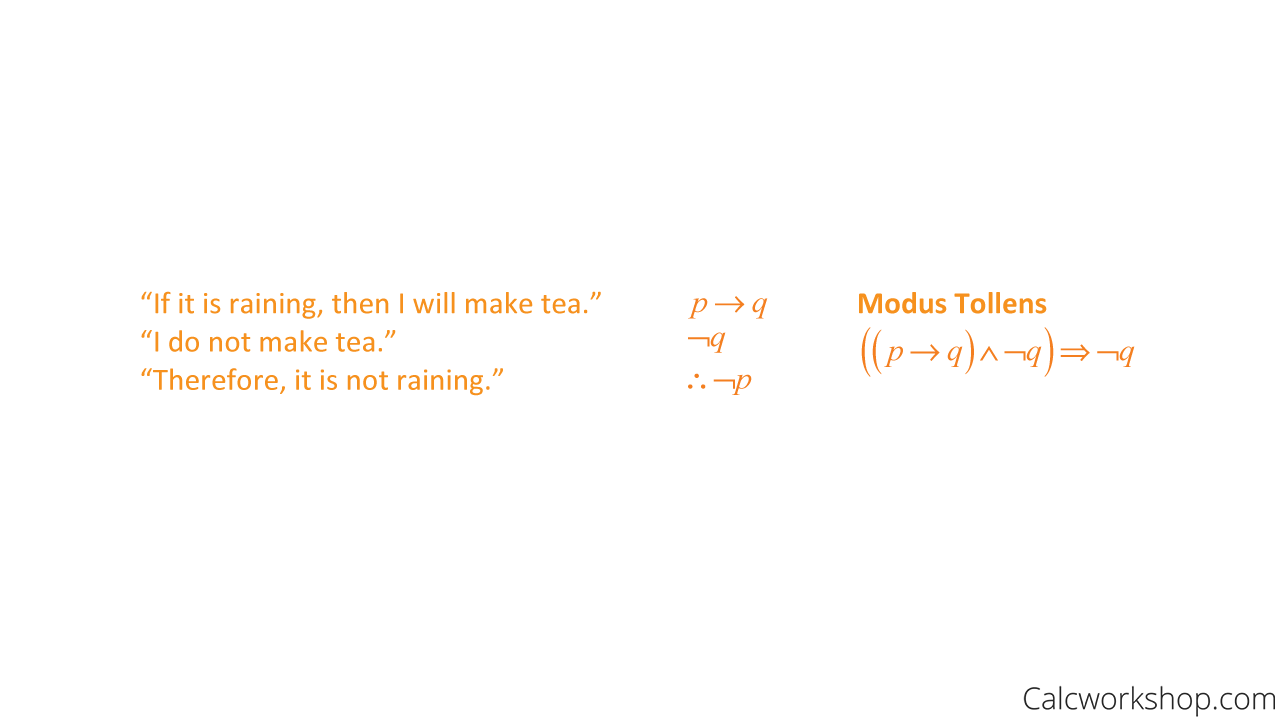
Modus Tollens — Example
Example — Hypothetical Syllogism
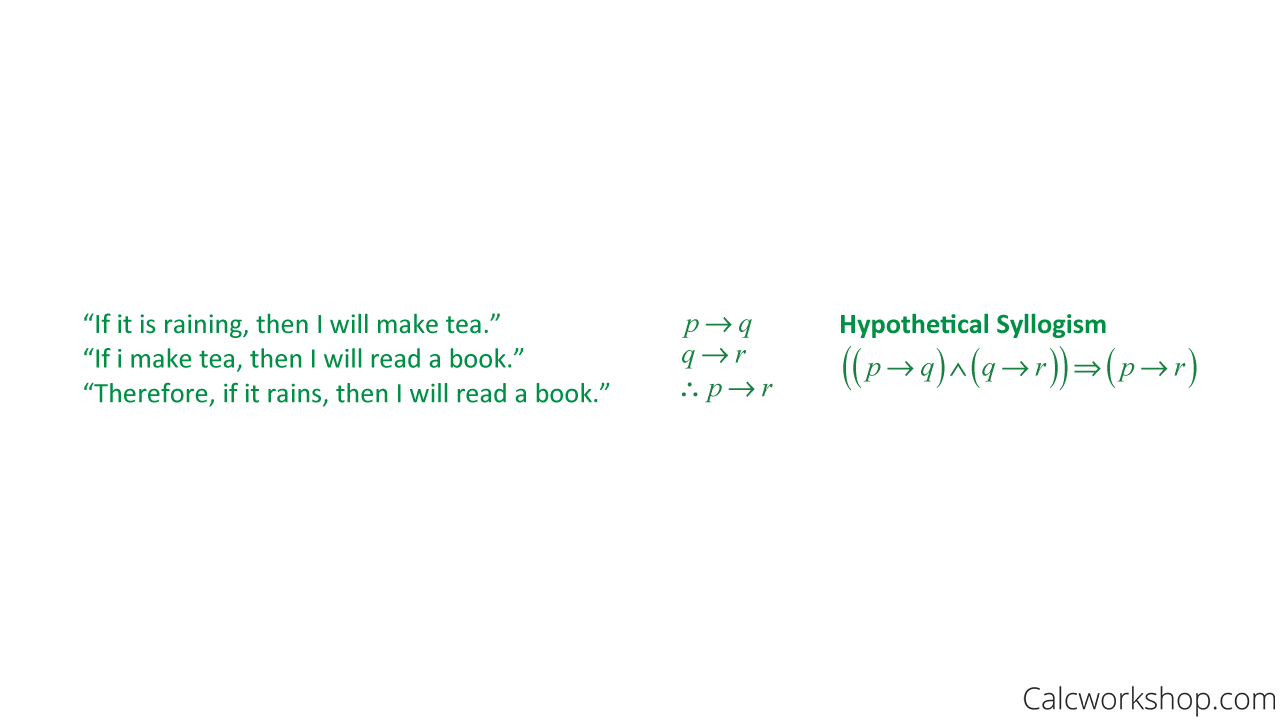
Hypothetical Syllogism — Example
Example — Disjunctive Syllogism
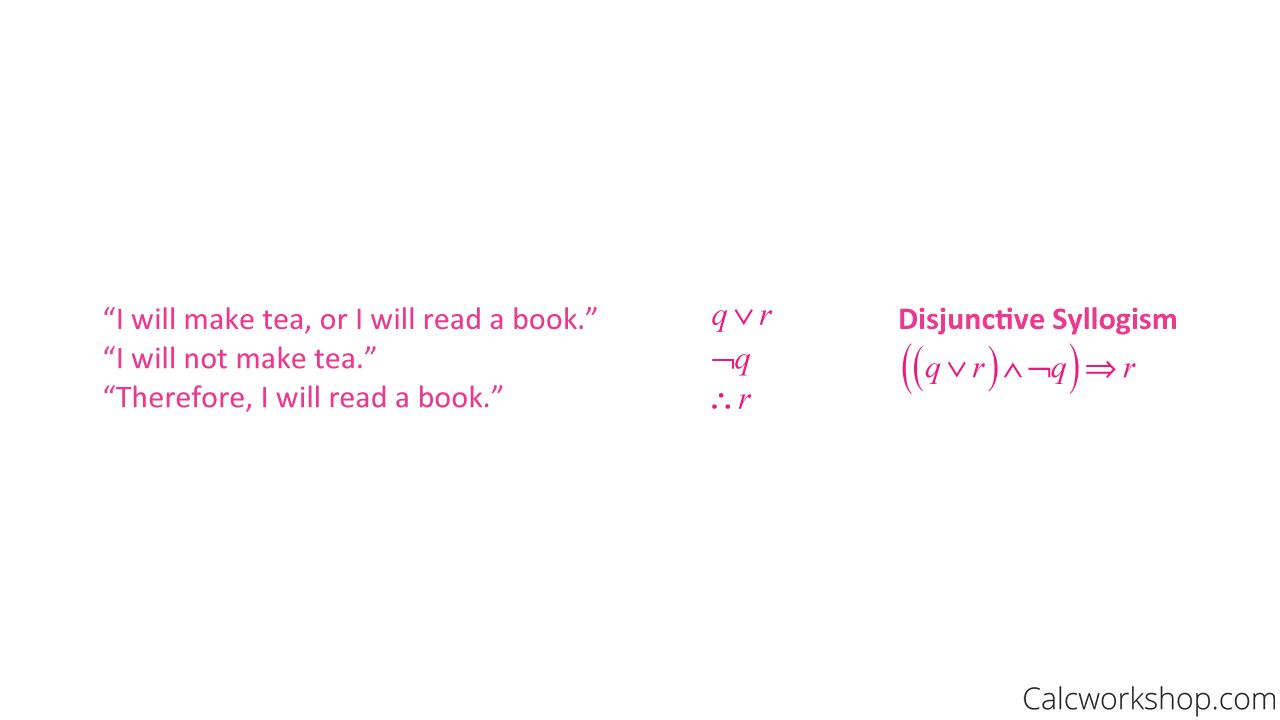
Disjunctive Syllogism — Example
Example — Addition
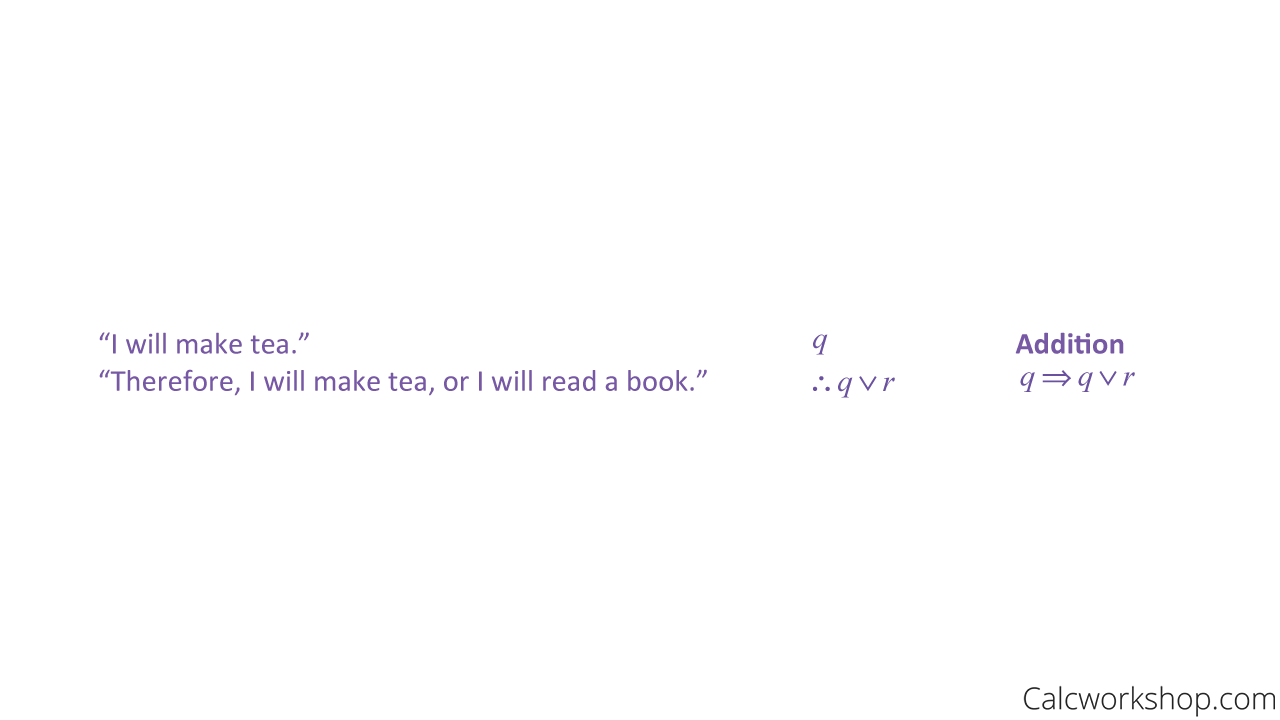
Rules Of Inference Addition — Example
Example — Simplification

Simplification Discrete Math — Example
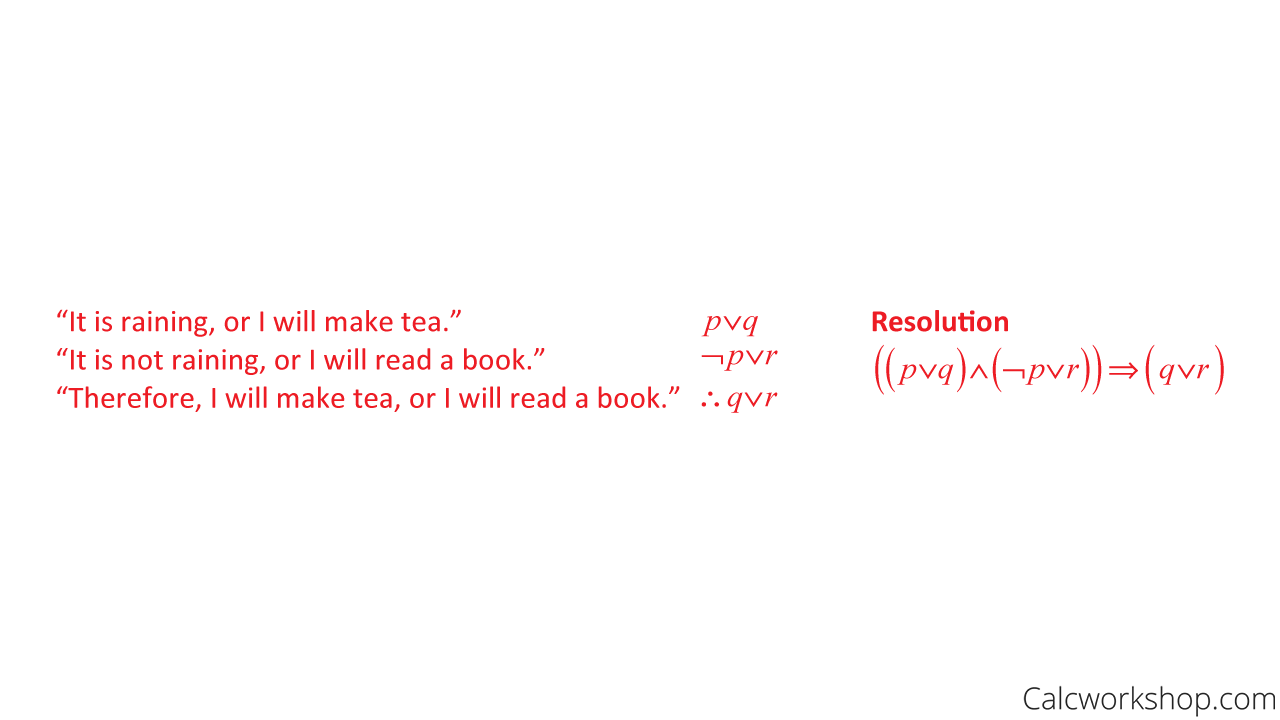
Discrete Math Resolution — Example
Valid Vs Invalid Argument
Alright, so now let’s see if we can determine if an argument is valid or invalid using our logic rules.
Test the validity of the argument:
- If it snows, Paul will miss class.
- Paul did not miss class.
- Therefore, it did not snow.
First, we will translate the argument into symbolic form and then determine if it matches one of our rules.
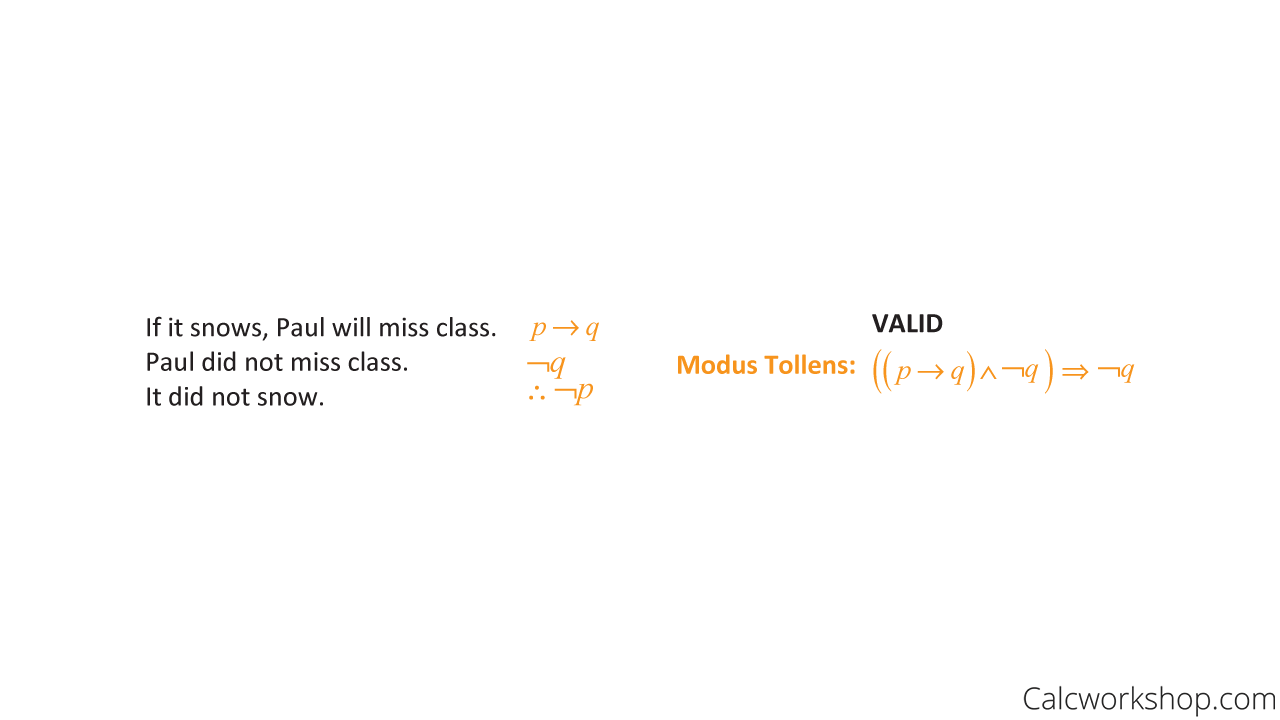
Example Of Modus Tollens Argument
Because the argument matches one of our known logic rules, we can confidently state that the conclusion is valid.
Let’s look at another example.
Test the validity of the argument:
- If it snows, Paul will miss class.
- It did not snow.
- Therefore, Paul did not miss class.
So, now we will translate the argument into symbolic form and then determine if it matches one of our rules for inference.
Because the argument does not match one of our known rules, we determine that the conclusion is invalid.
Here’s a big hint…
…translating arguments into symbols is a great way to decipher whether or not we have a valid rule of inference or not.
Discrete Math Quantifiers
But what about the quantified statement? How do we apply rules of inference to universal or existential quantifiers?
A quantified statement helps us to determine the truth of elements for a given predicate. And if we recall, a predicate is a statement that contains a specific number of variables (terms).
There are types of quantifiers:
- Universal Quantification (all, any, each, every)
- Existential Quantification (there exists, some, at least one)
And what you will find is that the inference rules become incredibly beneficial when applied to quantified statements because they allow us to prove more complex arguments.
Let’s look at the logic rules for quantified statements and a few examples to help us make sense of things.

Quantified Statement
It is essential to point out that it is possible to infer invalid statements from true ones when dealing with Universal Generalization and Existential Generalization. So, we have to be careful about how we formulate our reasoning.
For example, suppose we said:
- “Lily is a gymnast.”
- “Therefore, all women are gymnasts.”
This line of reasoning is over-generalized, as we inferred the wrong conclusion, seeing that not all women are a gymnast.
Lewis Carroll – Example
Okay, so let’s see how we can use our inference rules for a classic example, complements of Lewis Carroll, the famed author Alice in Wonderland.
- “All lions are fierce.”
- “Some lions do not drink coffee.”
- “Some fierce creatures do not drink coffee.”
So, this means we are given to premises, and we want to know whether we can conclude “some fierce creatures do not drink coffee.”
Let’s let L(x) be “x is a lion,” F(x) be “x is fierce,” and C(x) be “x drinks coffee.”
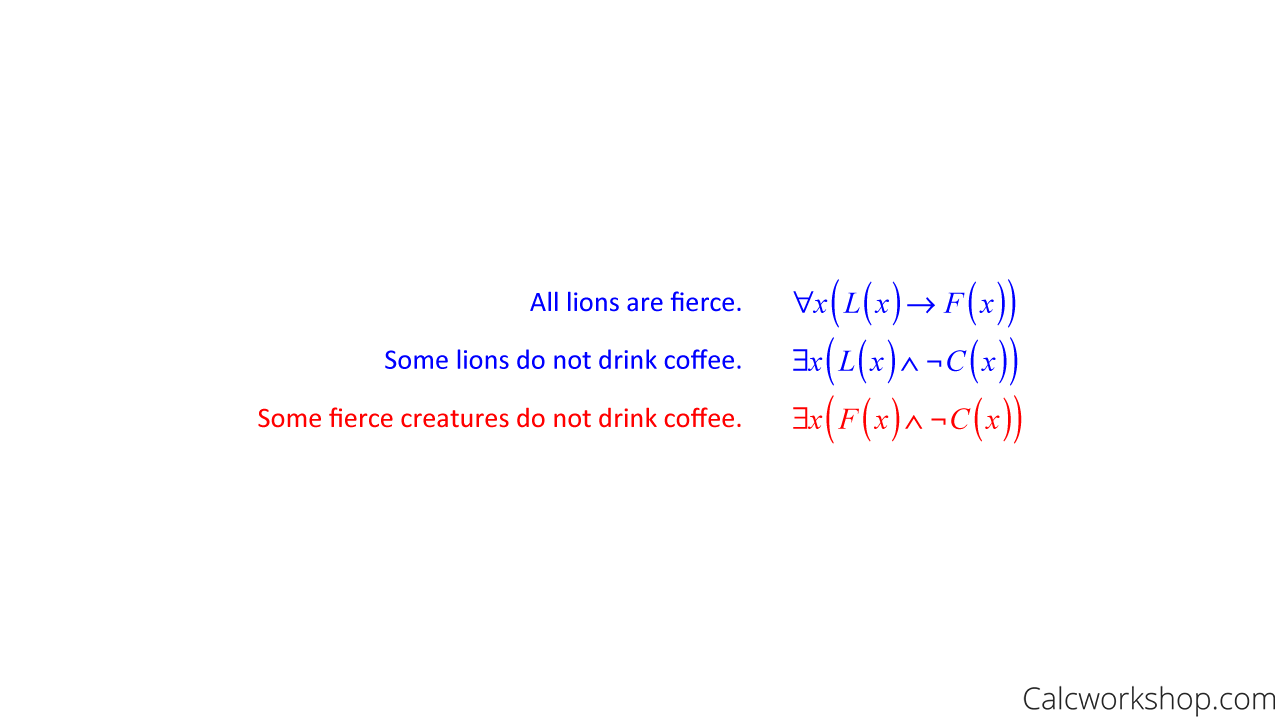
Lewis Carroll Logic — Example
But the problem is, how do we conclude the last line of the argument from the two given assertions?
If we can prove this argument is true for one element, then we have shown that it is true for others.
Let’s let Lambert be our element. This means that Lambert is a lion who is fierce and doesn’t drink coffee.

Proof Quantified Statements
We did it! By using a particular element (Lambert) and proving that Lambert is a fierce creature that does not drink coffee, then we were able to generalize this to say, “some creature(s) do not drink coffee.”
Together we will use our inference rules along with quantification to draw conclusions and determine truth or falsehood for arguments.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 33 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.