Did you know that the construction of mathematical arguments using compound propositions with the same truth value is used extensively in mathematics and forms the basis for logical equivalence?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
A proposition that is always true regardless of the truth values of the propositional variables it contains is called a tautology.
A compound proposition that is always false is called a contradiction or absurdity.
And a compound proposition that is neither a tautology nor a contradiction is referred to as a contingency.
But what does this really mean?
The following truth table will help to make sense of this.
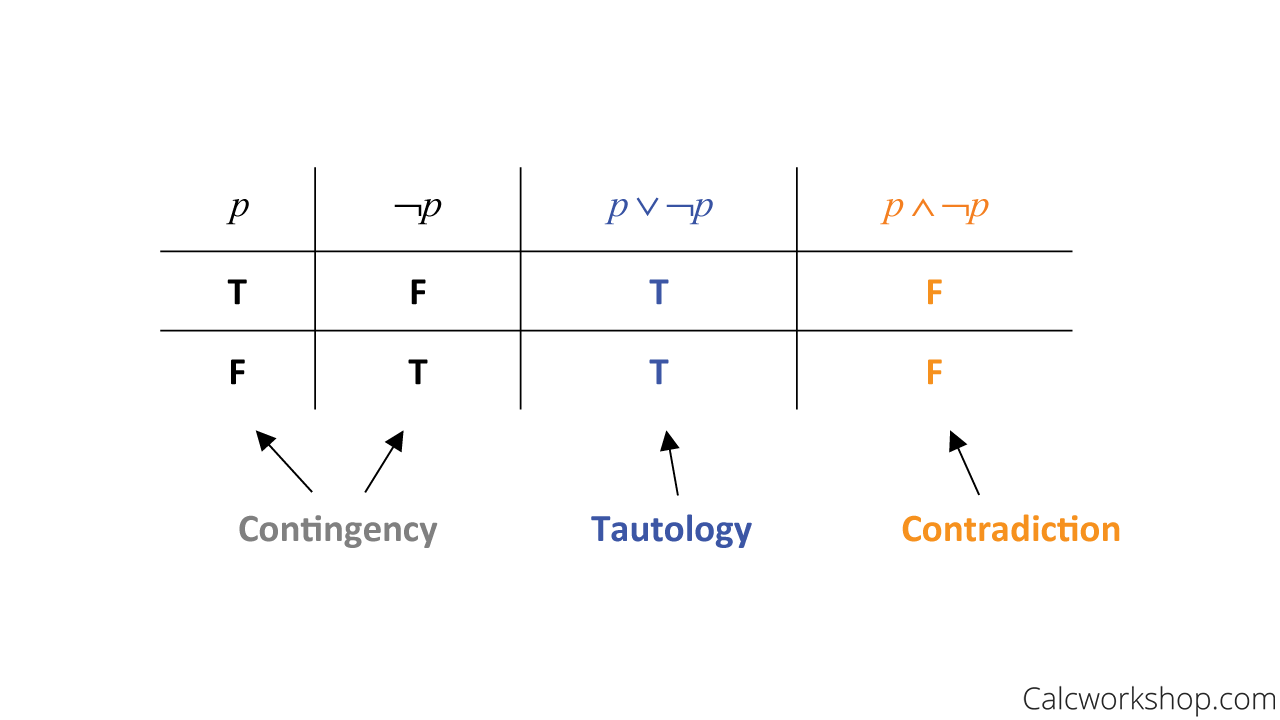
Tautology — Contradiction — Contingency
Okay, so a tautology, usually denoted by a bold-faced capital T, is when an entire column is all true as noted by Oak Ridge National Laboratory. A contradiction, traditionally represented with a bold-faced capital F, is when the whole column is all false. That means that a contingency is when a column is mixed with trues and falses.
But why would this be important?
Because tautologies and contradictions are essential in proving or verifying mathematical arguments, they help us to explain propositional equivalences — statements that are equal in logical argument. And it will be our job to verify that statements, such as p and q, are logically equivalent.

Logically Equivalent Statement
And the easiest way to show equivalence is to create a truth table and see if the columns are identical, as the example below nicely demonstrates
Logical Equivalence Laws
Below is a list of important equivalences laws, sometimes called the law of the algebra of propositions, that we will use throughout this course.

Laws Of Propositional Logic

Laws Of Logic
Similarly, there are some very useful equivalences for compound propositions involving implications and biconditional statements, as seen below.

Conditional Equivalence Laws
Equivalence Laws Biconditional
Examples
Okay, so let’s put some of these laws into practice.
Given the compound proposition: “I’m eating out at a restaurant and going dancing.”
Using De Morgan’s Laws, we can express the negation as “I’m not eating out at a restaurant, or I’m not going dancing.”
Notice that we negated both simple propositions and changed the “and” to an “or.”
Now, consider the following statement: If Ryan gets a pay raise, then he will take Allison to dinner.
This means we can also say that If Ryan does not take Allison to dinner, then he did not get a pay raise is logically equivalent.
Being able to change one proposition for another and maintain its truth value is extremely important.
For example, consider the following statement, “It is not true that Henry is a teacher and Paulos is an accountant.”
In symbols, this translates to:

Negation Rule — Example
Therefore, an equivalent statement would be of the form.

Demorgan Rule — Example
Hence, we would say, Henry is not a teacher or Paulos is not an accountant.
Furthermore, there are times when we would instead state reasons for why two statements are logically equivalent, rather than constructing a truth table.
In doing so, we transform the left-hand side of the statement to match the right-hand side, and we provide reasons for each transformation, similar to constructing a two-column proof in geometry. These logic proofs can be tricky at first, and will be discussed in much more detail in our “proofs” unit.
Throughout this lesson, we will learn how to write equivalent statements, feel comfortable using the equivalence laws, and construct truth tables to verify tautologies, contradictions, and propositional equivalence.
Logical Equivalence – Lesson & Examples (Video)
1 hr 4 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.