What is categorical syllogism?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s exactly what you’re going to learn in today’s discrete math lesson!
Let’s go.
So categorical syllogism is a form of deductive reasoning with three categorical propositions:
- Two Premises — that are assumed to be true.
- One Conclusion.
And our job is to determine the truth or fallacy of the argument.
In other words, a categorical proposition is deemed valid only if the premises are sufficient to prove the conclusion is true.
Now, there are four types of propositions that are used in syllogisms:
- Positive Universal: “all are…”
- Negative Universal: “none are…”
- Positive Existential: “some are…”
- Negative Existential: “some are not…”
And for categorical syllogism, three of these types of propositions will be used to create an argument in the following standard form as defined by Wikiversity.
- Major Premise (universal quantifier)
- Minor Premise (existential quantifier)
- Conclusion (universal or existential)
For example:
- Major Premise: “All philosophers are thinkers.”
- Minor Premise: “Some philosophers are teachers.”
- Conclusion: “Some thinkers are teachers.”
Alright, so now that we know the framework for writing categorical syllogism in standard form, it’s now time to talk about its mood.
The mood of a categorical syllogism corresponds to three letters (A,E,I, or O) that represent the proposition types found in the argument, listed in order as they appear in standard form

Quantifier Mood
So, for the above example with the philosophers, the mood for this argument would be: AII
Okay, some instructors will tend to focus on identifying the mood of the categorical syllogism as it is a way to determine truth of falsehood.
But, to be perfectly honest, we have enough to memorize as it is, don’t you think? So, instead of getting bogged down with memorizing which three-letter combinations are valid or invalid, we’re going to diagram categorical syllogism using something similar to Venn Diagrams in order to determine validity.
Besides, I like to think that the idiom “a picture is worth a thousand words,” definitely rings true here!
Steps for Diagramming Categorical Syllogism
- Draw three overlapping circles to represent the three variables, or elements, in the argument and label them.
- Use shading to diagram the Universal statement(s), by shading any region that is known to contain NO ELEMENTS.
- Focusing now on the unshaded region, we use an ‘X” to diagram Existential statements.
- Now we check to see if the diagram verifies the conclusion, knowing that if a region doesn’t contain any markings or shading, then it is uncertain whether or not that region contains any elements.
-If a region is known to contain at least one element, then we place an “X” in that region
-If we are not certain which of two regions contains the element(s), then we place the “X” on the boundary between those two regions.
This may seem confusing at first, but after working through examples it will all become clear!
Three Overlapping Circles
Example #1
- “All philosophers are thinkers.”
- “Some philosophers are teachers.”
- “Some thinkers are teachers.”
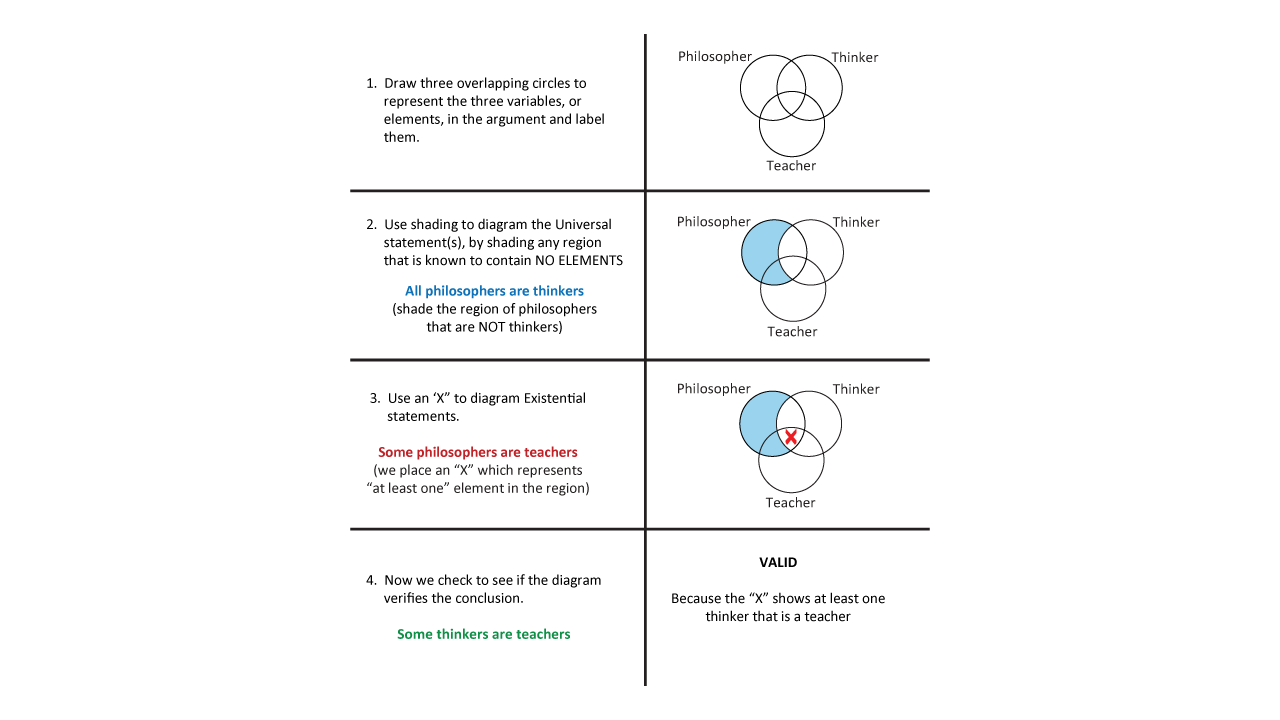
Valid Categorical Syllogism Example
So, after diagramming categorical syllogism we are able to conclude that this argument is valid.
Example #2
Okay, now let’s suppose the following argument
- “Some eagles are not fish.”
- “No fish are birds.”
- “Some eagles are not birds.”
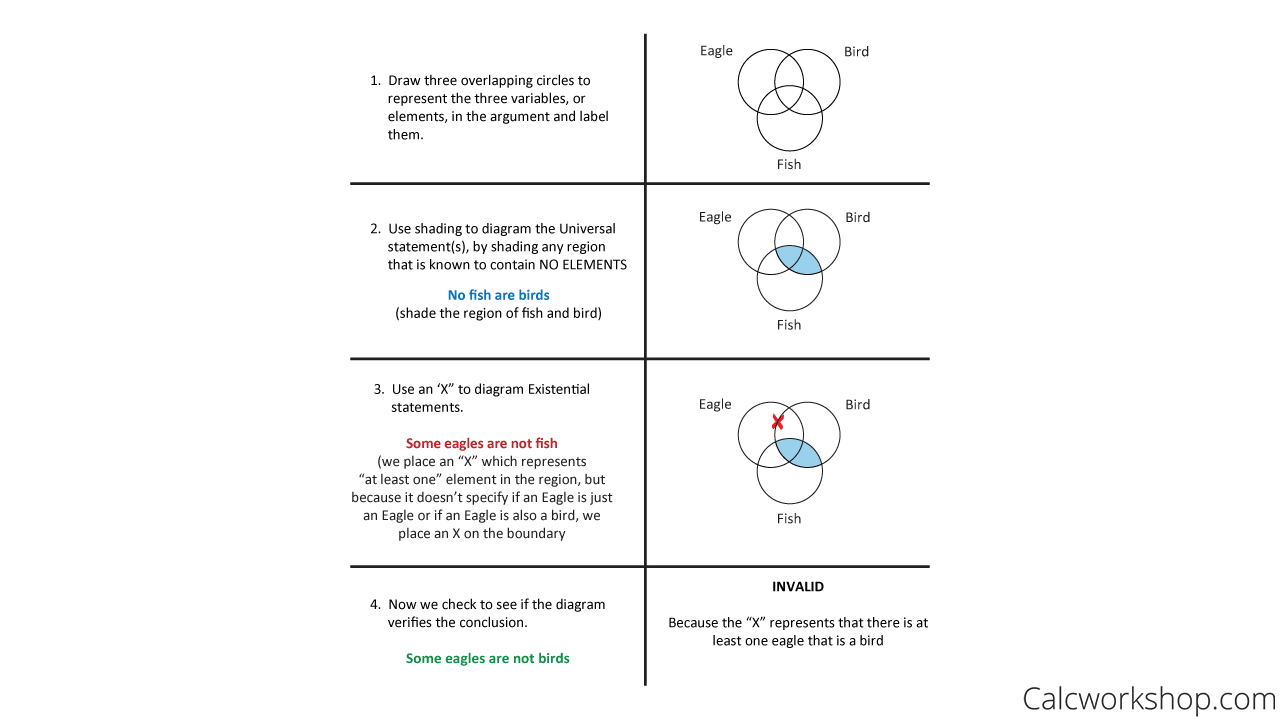
Invalid Argument Logic
This statement is invalid because we are uncertain about the conclusion.
We will look at countless examples of how to diagram categorical logic for all different types of scenarios and see how easy it is to set up and decipher.
Let’s do it!
Categorical Syllogism – Lesson & Examples (Video)
58 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.