Linear Transformations

Have you ever tried to peer through a dirty window? Have your glasses, sunglasses, or possibly your car windshield been so fogged up that you can’t see through? Isn’t trying to understand what’s on the other side difficult in times like this?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

As we learned in previous lessons, shifting our focus from a system of equations to vector or even matrix equations helps us better analyze the solution and provide a better view. We never actually changed the linear system; we just wrote it in such a way as to make it easier to see – we cleaned it up a bit or turned on the defrost.

However, there are other times when a simple defogging isn’t enough, and we need a bit more “umff!” and a little more action. We don’t just want to clean it up, but to truly transform it!

Matrix Equations and Transformations

The matrix equation $A \vec{x} = \vec{b}$ gains power when we think of the matrix $A$ as an object that “acts” on a vector $\vec{x}$ through multiplication; thus, causing a transformation or mapping.

Connections Between Geometry and Linear Algebra

Do you remember how in geometry, we learned that transformations occur when there is a change in size, shape, or position (i.e., dilation, rotation, reflection, and translation)? Now you may wonder, how does our knowledge of geometry and transformation relate to linear algebra?

Great question! Let’s dive into it.

Transformation is a function or mapping that takes an input and produces an output. The fascinating part is that this transformation can be expressed by a matrix and interpreted similarly.
Confused? Let’s break it down. Just like $f (x) = \sqrt{x}$ is a function that accepts a value, x, as its input and spits out the square root of that number (i.e., $f (9) = \sqrt{9} = 3$ , where the input is 9, and the output is 3), matrices behave the same as functions.

Matrix as Functions

Therefore, $A \vec{x} = \vec{b}$ , similar to $y = f (x)$ , can be thought of as a function where $A$ is the function with independent variable $\vec{x}$ (i.e., input) and $\vec{b}$ is the dependent variable (output). This means $A$ performs an action similar to how the square root acts on a number and transforms one real number into another.

Transformations in Linear Algebra

So, a transformation $T$ is a rule or action that assigns to each vector $\vec{x}$ in $R^{n}$ a vector $T (\vec{x})$ in $R^{m}$ . Thus, we can define the following:
$\begin{aligned} R^{n} & is the domain of T \\ R^{m} & is the codomain of T \\ T (\vec{x}) & in R^{m} is the image of \vec{x} under T \\ {T (\vec{x}) : \vec{x} in R^{n}} & in R^{m} is the range of T \end{aligned}$

Codomain and Range

Wait! What’s the difference between codomain and range? Aren’t they the same thing?

Well, in your previous courses, the range and the codomain probably were the same, but the distinction is quite important as you progress in mathematics. The codomain is all the possible outcomes, while the range is all the actual outcomes (images) that appear after the transformation.

So, if $T (\vec{x}) = A \vec{x}$ where $A$ is an m x n matrix, then a matrix transformation, which is sometimes abbreviated by $\vec{x} \mapsto A \vec{x}$ , behaves something like this:

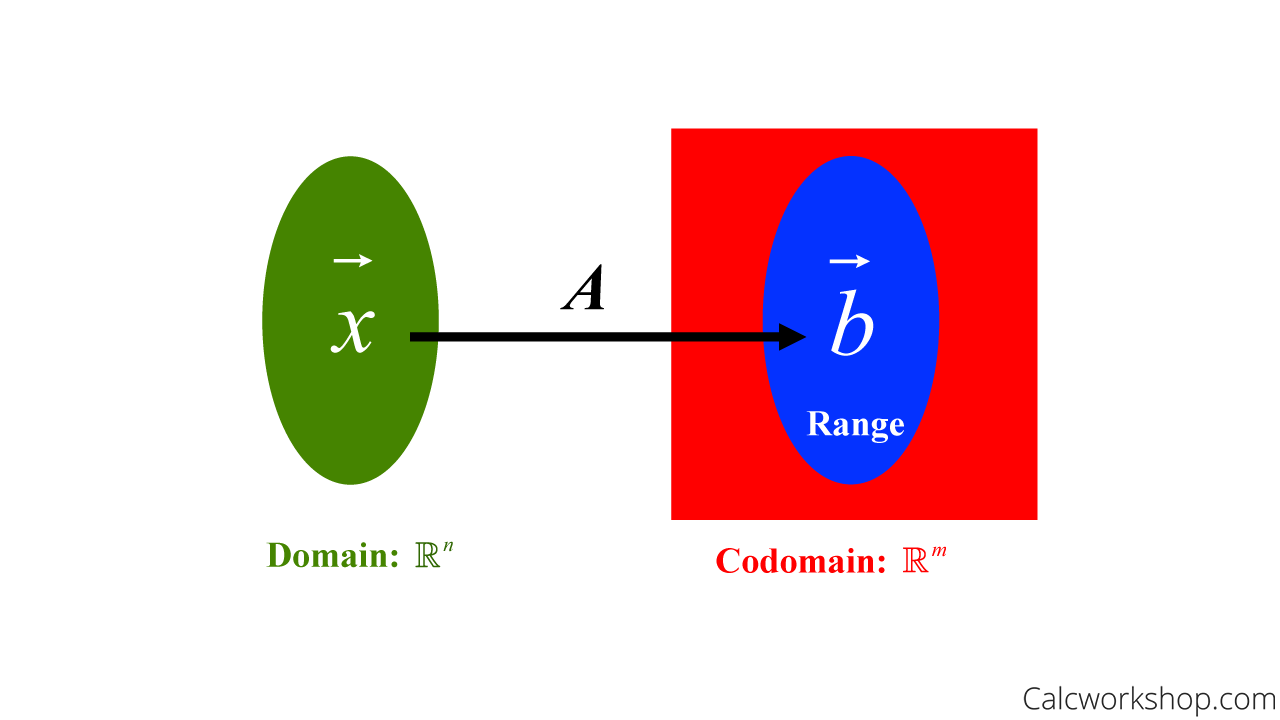
Matrix Transformation Mapping

The green oval is the input value, the red square is all the possible outcomes, and the blue oval represents the range, all the actual outputs (images) that are calculated after the transformation A.

More specifically, if A is an mxn matrix, and $T (\vec{x}) = A \vec{x}$ is the matrix transformation, then:

The domain of $T$ is the number of columns (n) of A
The codomain is the number of rows (m) of A
The range is the column space of A

Don’t worry about understanding “column space” for now…we’ll come back to it in a future lesson, but for now, just know that the range of $T$ is the set of all linear combinations $s$ of the columns of A.

Also, it may be helpful to point out that some textbooks refer to matrix A as the standard matrix for the linear transformation $T$ .

One-to-One and Onto Transformations

Now it’s time to talk about one-to-one (also known as injective) and onto (also known as surjective) transformations.

For a function to be one-to-one, every distinct element in the domain has a distinct image in the codomain. All this means is that every element in the domain (the green oval from the diagram above) maps to a “unique buddy” in the codomain.

Definition: A mapping $T : R^{n} \to R^{m}$ is said to be one-to-one if each $\vec{b}$ in $R^{m}$ is the image of at most one $\vec{x}$ in $R^{n}$ .

Now, an onto function is when every element in the codomain is mapped to by at least one element in the domain. Which means nothing in the codomain is left out. Simply put, an onto function is when the range equals the codomain (the blue oval is the same as the red square)!

Definition: A mapping $T : R^{n} \to R^{m}$ is said to be onto if each $\vec{b}$ in $R^{m}$ is the image of at least one $\vec{x}$ in $R^{n}$ .

Here’s a tip for keeping this straight … focus on the codomain and ask yourself how often each element gets mapped to, or as I like to say, how often each element gets “hit” or tagged.

Injective (one-to-one): elements in the codomain get “hit” at most once
Surjective (onto): elements in the codomain get “hit” at least once

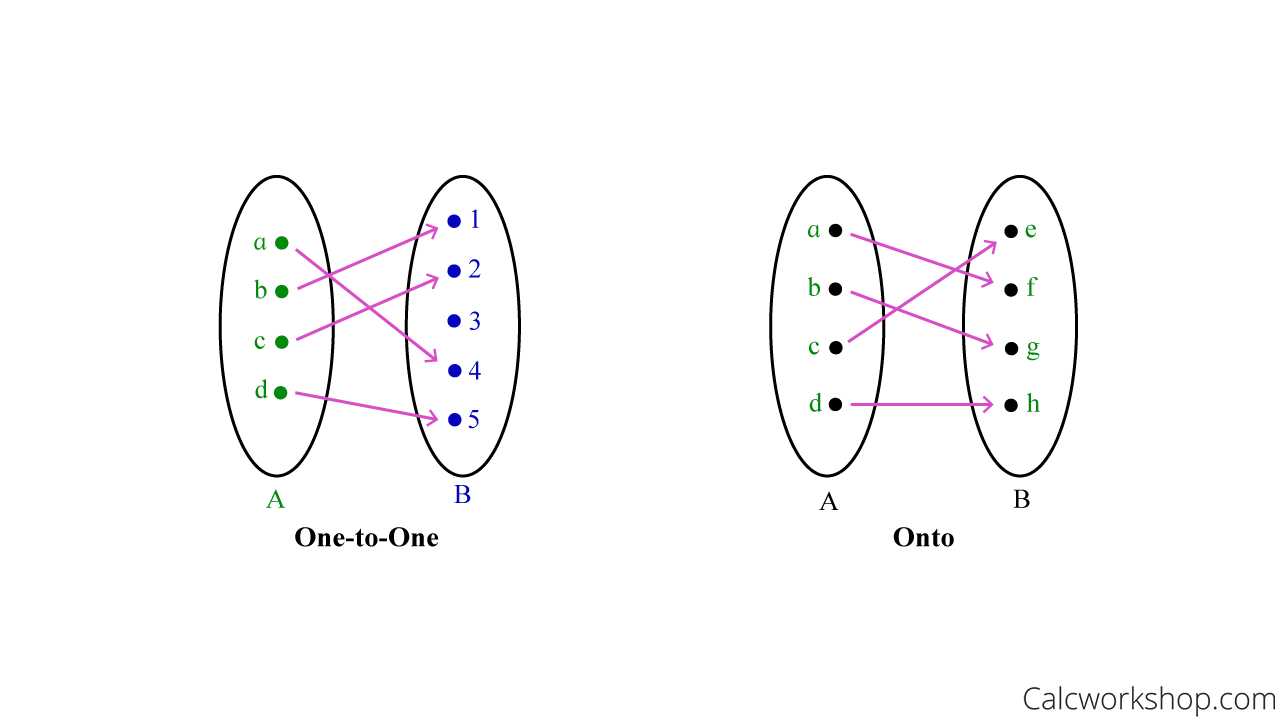
One To One vs. Onto Mapping

Matrix Transformation Theorems

We have special theorems for one-to-one matrix transformations and onto matrix transformations that will help us perform and identify linear transformations.

One-to-One Matrix Transformation Theorem: If $A$ is an mxn matrix and let $T (\vec{x}) = A \vec{x}$ be a matrix transformation, then the following statements are equivalent:

$T$ is one-to-one
For every $\vec{b}$ in $R^{m}$ , the equation $T (\vec{x}) = \vec{b}$ has at most one solution
For every $\vec{b}$ in $R^{m}$ , the equation $A \vec{x} = \vec{b}$ has a unique solution or is inconsistent $A \vec{x} = \vec{0}$ has only the trivial solution (zero vector)
The columns of $A$ are linearly independent
$A$ has a pivot in every column.
The range of $T$ has dimension $n$ .

Onto Matrix Transformation Theorem: If $A$ is an mxn matrix and let $T (\vec{x}) = A \vec{x}$ be a matrix transformation, then the following statements are equivalent:

$T$ is onto
$T (\vec{x}) = \vec{b}$ has at least one solution for every $\vec{b}$ in $R^{m}$
$A \vec{x} = \vec{b}$ is consistent for every $\vec{b}$ in $R^{m}$
The columns of $A$ span $R^{m}$
$A$ has a pivot in every row.
The range of $T$ has dimension $m$ .

Linear Transformations

Okay, now that we’ve gotten all our definitions and theorems, let’s learn how to verify, identify, and compute linear and matrix transformations.

Don’t worry. You already have a leg up because of your geometry transformations (reflections, rotations, translation, and dilations).

Examples of Matrix Transformations

So, a transformation $T : R^{n} \to R^{m}$ is linear if:

$T (\vec{u} + \vec{v}) = T (\vec{u}) + T (\vec{v})$ for all $\vec{u}, \vec{v}$ in the domain of $T$
$T (c \vec{u}) = c T (\vec{u})$ for all $\vec{u}$ and scalars $c$

This means that every linear transformation preserves the operations of vector addition and scalar multiplication. And why is this important? Because every linear transformation is a matrix transformation.

Moreover, a linear transformation is our formula or “action” that allows us to dilate, reflect, rotate, shear, project, and rotate, just like we did with objects in geometry!

Dilation, Reflection, and Shear Examples

Okay, so let’s look at a few examples to help us understand matrix transformations.

Example of a Dilation: If $T : R^{2} \to R^{2}$ where $T (\vec{x}) = 0.25 x$ . Find a standard matrix A for $T$ .

We obtain the columns of $A$ by evaluating $T$ on the standard coordinate vectors $e_{1}, e_{2}$ which are the columns of the $2 \times 2$ identity matrix.

$\begin{aligned} T (e_{1}) & = 0.25 e_{1} \\ = 0.25 [\begin{matrix} 1 \\ 0 \end{matrix}] \\ = [\begin{array}{c} 0.25 \\ 0 \end{array}] \\ T (e_{2}) & = 0.25 e_{2} \\ = 0.25 [\begin{matrix} 0 \\ 1 \end{matrix}] \\ = [\begin{array}{cc} 0 \\ 0.25 \end{array}] \\ A & = [\begin{array}{cc} T (e_{1}) & T (e_{2}) \end{array}] \\ = [\begin{array}{cc} 0.25 & 0 \\ 0 & 0.25 \end{array}] \end{aligned}$

Example of a Reflection

Find the standard matrix A for $T$ if (a) $T : R^{2} \to R^{2}$ reflects through the vertical axis, and (b) $T : R^{2} \to R^{2}$ reflects through the horizontal axis.

Just like we did for the previous example, we will be obtaining the columns of A by evaluating $T$ on the standard coordinate vectors $e_{1}, e_{2}$ which are the columns of the $2 \times 2$ identity matrix. But rather than multiplying by a constant will need to be a bit savvy with our application.

When it says to reflect through the “vertical axis, ” we reflect over the y-axis. So, the $x$ -values will change signs while the $y$ -values will stay the same.

$[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}] \underset{reflect through x_{2} -axis}{\to} [\begin{array}{cc} - 1 & 0 \\ 0 & 1 \end{array}]$

And when it says to reflect through the “horizontal axis,” that means we are reflecting over the $x -$ axis. So, the $x$ -values will stay the same, but the $y$ -values will change signs.

$[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}] \underset{reflect through x_{1} -axis}{\to} [\begin{array}{cc} 1 & 0 \\ 0 & - 1 \end{array}]$

Example of a Shear

Find the standard matrix $A$ for $T$ if (a) $T : R^{2} \to R^{2}$ is a vertical shear transformation that maps $e_{1}$ into $e_{1} - 3 e_{2}$ and leaves $e_{2}$ unchanged, and (b) $T : R^{2} \to R^{2}$ is a horizontal shear transformation that maps $e_{2}$ into $e_{2} + 5 e_{1}$ and leaves $e_{1}$ unchanged,

Alright, so we obtain the columns of $A$ by evaluating $T$ on the standard coordinate vectors $e_{1}, e_{2}$ which are the columns of the $2 \times 2$ identity matrix, using the fact that $e_{1}$ changes to $e_{1} - 3 e_{2}$ and $e_{2}$ remains the same.

$\begin{aligned} T (e_{1}) & = e_{1} - 3 e_{2} \\ = [\begin{matrix} 1 \\ 0 \end{matrix}] - 3 [\begin{matrix} 0 \\ 1 \end{matrix}] \\ = [\begin{matrix} 1 \\ 0 \end{matrix}] - [\begin{matrix} 0 \\ 3 \end{matrix}] \\ = [\begin{matrix} 1 \\ - 3 \end{matrix}] \\ T (e_{2}) & = e_{2} \\ = [\begin{matrix} 0 \\ 1 \end{matrix}] \\ A & = [\begin{array}{ll} T (e_{1}) & T (e_{2}) \end{array}] \\ = [\begin{array}{ll} 1 & 0 \\ - 3 & 1 \end{array}] \end{aligned}$

Example of a Rotation

Find the standard matrix $A$ for $T$ if $T : R^{2} \to R^{2}$ rotates each point about the origin through $\frac{3 π}{2}$ .

Okay, so for rotations, we will use the fact that:

$\begin{aligned} T (e_{1}) & = [\begin{array}{c} \cos θ \\ \sin θ \end{array}] \\ T (e_{2}) & = [\begin{array}{c} - \sin θ \\ \cos θ \end{array}] \end{aligned}$

Therefore,

$\begin{aligned} A & = [\begin{array}{ll} T (e_{1}) & T (e_{2}) \end{array}] \\ = [\begin{array}{cc} \cos θ & - \sin θ \\ \sin θ & \cos θ \end{array}] \end{aligned}$

And if $θ = \frac{3 π}{2}$ , then the standard matrix A is calculated as follows:

$\begin{aligned} A & = [\begin{array}{cc} \cos (\frac{3 π}{2}) & - \sin (\frac{3 π}{2}) \\ \sin (\frac{3 π}{2}) & \cos (\frac{3 π}{2}) \end{array}] \\ = [\begin{array}{cc} 0 & - (- 1) \\ 1 & 0 \end{array}] \\ = [\begin{array}{cc} 0 & 1 \\ - 1 & 0 \end{array}] \end{aligned}$

Example

Show that $T$ is a linear transformation by finding a matrix that implements the mapping $T (x_{1}, x_{2}, x_{3}, x_{4}) = (0, x_{1} + 2 x_{2}, 3 x_{2} + 4 x_{3}, 5 x_{3} + x 6_{4})$

First, we must recognize that $T$ is a mapping from $R^{4} \to R^{4}$ . Next, we will obtain the columns of $A$ by evaluating $T$ on the standard coordinate vectors $e_{1}, e_{2}, e_{3}, e_{4}$ which are the columns of the $4 \times 4$ identity matrix as follows:

$\begin{array}{r} \begin{aligned} T (e_{1}) & = T (\underset{x_{1}}{1}, \underset{x_{2}}{0}, \underset{x_{3}}{0}, \underset{x_{4}}{0}) \\ = (0, (1) + 2 (0), 3 (0) + 4 (0), 5 (0) + 6 (0)) \\ = (0, 1, 0, 0) \end{aligned} \end{array}$

$\begin{array}{r} \begin{aligned} T (e_{2}) & = T (\underset{x_{1}}{0}, \underset{x_{2}}{1}, \underset{x_{3}}{0}, \underset{x_{4}}{0}) \\ = (0, (0) + 2 (1), 3 (1) + 4 (0), 5 (0) + 6 (0)) \\ = (0, 3, 3, 0) \end{aligned} \end{array}$

$\begin{array}{r} \begin{aligned} T (e_{3}) & = T (\underset{x_{1}}{0}, \underset{x_{2}}{0}, \underset{x_{3}}{1}, \underset{x_{4}}{0}) \\ = (0, (0) + 2 (0), 3 (0) + 4 (1), 5 (1) + 6 (0)) \\ = (0, 0, 4, 5) \end{aligned} \end{array}$

$\begin{array}{r} \begin{aligned} T (e_{4}) & = T (\underset{x_{1}}{0}, \underset{x_{2}}{0}, \underset{x_{3}}{0}, \underset{x_{4}}{1}) \\ = (0, (0) + 2 (0), 3 (0) + 4 (0), 5 (0) + 6 (1)) \\ = (0, 0, 0, 6) \end{aligned} \end{array}$

$\begin{array}{r} A = [\begin{array}{llll} T (e_{1}) & T (e_{2}) & T (e_{3}) & T (e_{4}) \end{array}] = [\begin{array}{llll} 0 & 0 & 0 & 0 \\ 1 & 3 & 0 & 0 \\ 0 & 3 & 4 & 0 \\ 0 & 0 & 5 & 6 \end{array}] \end{array}$

See, transformations are pretty easy, right?

Next Steps

I understand this is a lot of information to process, but there’s no need to worry. You will:

Learn all the definitions and theorems, connecting each to its geometric interpretation.
Explore numerous examples in depth.
Master the ability to explain, identify, and construct linear and matrix transformations!

It’s time for you to dive in!

Video Tutorial w/ Full Lesson & Detailed Examples

linear-transformations-example

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

4.9 / 5

1,128 Reviews

Kevin S.10-30-24 - CO, United States

I had never even heard of discrete math before I had to take it for my Bachelor's in Cybersecurity. I had actually hoped that my math days were done! I suffered through class not understanding any of the presentations until I stumbled across Calcworkshop. I used the Calcworkshop lessons more than I used my instructor's lectures and my book. I ended up with a high B (just 12 points away from an A) thanks to Jenn. Without her easy to understand style of teaching, I'm not sure I would have even passed the class. Thank you so much!!!

Richard10-29-24 - Norway

Very well structured and site. It is well structured giving a good overview of the different topics regarding all mathematics where you easily can choose which path is applicable to your specific needs.The video lectures are superb with introduction to the topic followed by a detailed theoretically explaination and what I personally get most out of is; heaps of examples where you are taken and shown, step by step, the prosess of solving the problem. They also includd practice sheets and solutions to test yourself after each chapter. There is a lot to undertake on this site, but it provides an easy and understandable interface to map out what you need to do. The site has been very helpfull for me and I highly recommend it.

RobWP10-26-24 - United States

I am taking this course for mainly linear algebra review. It is a course that I have had but fairly long ago. I'm currently working in masters in data science and linear algebra namely transformations is something that has come up and I thought I need a good review on. I so far what I have liked about the course is, the common sense approach. Her approach makes it easy to remember the concepts because of her common sense approach. I like the fact that she gives information that is not really in any textbooks. I can vouch for that because not only have I used textbook recently to review I have had a formal class in the past that used textbooks. She goes over things thoroughly and for the price it's very much worth it. I have had many quarters of formal calculus and differential equations courses and I am kind of anxious to look to see what her approach to calculus is. I can't really answer how this class would be for a novice or someone who has not had linear algebra the past, but I really don't think they need to worry about that. Her method I feel will make a novice be successful and to understand the material. She is very easy to understand. Gives good examples but doesn't beat a dead horse either. What I like about her introductory remarks is that she says what linear algebra is all about and she points out what the core of the linear algebra is about and what you need to know. Having taken it before I would have to agree and she is dead on spot.

Robbin03-18-25 - CO, United States

Very well organized, helpful and comprehensive. It is great also to have access to prior course material so you can easily go back and refresh if you need to. Jenn is very clear and the number of examples leaves one comfortable with each topic. Couldn't be happier.

RCJK03-07-25 - ID, United States

I had to take Calculus I and II as accelerated classes while working full time. It was my first time taking this courses and was very overwhelming. Calcworkshop really made learning the subjects easier for me by having all the subjects easy to find and easy to understand explanations. I received a B in both classes which I am extremely happy with doing the classes in double time.

Jacqueline S.03-07-25 - SC, United States

Jenn is awesome!Her breakdown of the topic is beyond what you would expect. She is showing you how to arrive at the answer instead of doing a simple equation. Most people need to know the why it give confidence and structure to the learning process. This is what Jenn is great at, she knows how to deliver the information to a non math mind in a way that instills knowledge that you can forever draw from as you move forward. It's really well thought out. She is a true master teacher. Thanks for all that you do for us! Hugs n Blessings... JS

Rose M.03-07-25 - CA, United States

Best instructor ever, I have never had Math explained in a way that was so interesting. Her lectures and instruction is explained perfectly, and I will continue to use this for all my future math courses.

A Reviewer03-07-25 - United States

I needed help with college precalculus, they provided more than enough help that allowed me to succeed and get the scores I needed.

Jujuana03-05-25 - MO, United States

I love the videos the way each lesson is explained step by step. I love that she has examples that you can go over again and again in order to understand the way algebra works. I was lost because my instructor was flying through each lesson and I was totally lost. I attached my syllabus and they helped me stay focus on what I was working and give me a guide to go back and refresh what I went over in class.

Stacey01-31-25 - AZ, United States

Hello, I highly recommend getting a subscription to Jenn and her Calcworkshop teaching math service. I did a general, "go from bad to good at math", Google search and found out about Calcworkshop through responses to the topic on reddit. I've just started watching her videos and found them to be extremely helpful. I'm going back to college after a long absence and math was never my strong suit. So I'm starting at the very bottom of her available subjects and going from there. Just watching a couple of the videos has taken me from being dragged along not understanding to following along just fine in my math class. I'm moving from the "I'll never get this", to the "I look forward to understanding this", mindset in approaching math. This for me is huge, and even though I have a long way to go, I'm confident I will get there thanks to Jenn. Totally worth it!

Kathy W.01-14-25 - WA, United States

Calcworkshop is an outstanding source to learn math and understanding math concepts. Jenn is an outstanding master teacher. Every lesson is clearly presented making understanding easy to grasp. Practice lessons with accompanying answers are given for each section. I am 82, a retired teacher and lifelong learner. Learning calculus has always been on my bucket list. Calcworkshop is helping me reach my goal.

Cheryl01-14-25 - NY, United States

Calc workshop is the absolutely best resource for math and I have seen almost everything that exists out there. I have even recommended it to my daughter's school so that all the kids could use the videos during the summer months for the subject they plan to study in the fall. They are guaranteed to get a A if they have watched the videos and completed the problems before taking the class. Students who are weak in areas can access lower level classes and those who seek to advance above grade level can do so. The videos and exercises are crystal clear and the excellent presentations raise the bar for teachers everywhere. I have always believed that one great math teacher is important in the education process. The videos, exercises and problems are excellent. It is not possible to have ANY knowledge gaps. I have never seen anything on the market that even begins to compete with it!

Justin N.12-22-24 - OK, United States

Calculus can be a scary subject. I know I was scared. I had been out of any math class for over 23 years. I had taken an 8 week Calculus 1 class and felt like I was overloaded. Going into Calculus 2 I found CALCWORKSHOP.com. I used the training videos and material to really dive back into Calc 1 and prepare for Calc 2. Long story short with the material provided and ample study time, I finished Calc 2 with a 95%. Thanks Jenn!

Shelby12-10-24 - OH, United States

CalcWorkshop was a wonderful resource as someone going onto a college calculus 1 class after not having taken a math course in a year! Jenn always explained things in a logical order that built upon previous lessons, and the way she explained topics was always easy to understand. Calcworkshop saved this semester for me, and I couldn't be more grateful to have found this site. :)

Jordan Q.12-09-24 - AR, United States

Anyone struggling with math at any level would greatly benefit from this product. I signed up for it immediately after getting a D on my first exam in calculus 2 and ended up getting A's and B's on the remaining exams, getting a B overall in the class. Jenn breaks down the topics, without skipping any steps, in a way that makes them very easy to understand. I highly recommend this product!

N8Booker11-28-24 - MA, United States

I'm in school to get my degree Networking and Cybersecurity and I'm in my first year. I've been away from school for quite a long time so the concepts that are being taught although not foreign to me, have so much dust on them from a lack of being used in real world applications regularly.I stumbled upon CalcWorkshop by pure chance and it has been a game changer for me. Jen filled in the gaps in between what my Professor is teaching at a rapid fire pace and where my brain grasps and applies it. If not for Jen's approach, I'd have failed my test I took miserably!Am I grateful? It goes beyond words and not I recommend her workshops to everyone!

Kevin S.10-30-24 - CO, United States

Richard10-29-24 - Norway

RobWP10-26-24 - United States

RCJK03-07-25 - ID, United States

Jacqueline S.03-07-25 - SC, United States

See more reviews on Shopper Approved