What’s the difference between “I have to” and “I get to”?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Well, the first one implies a role or job that must be performed. It means a duty or responsibility. But the second phrase, “I get to,” shifts the perspective from a simple task that must be completed to something much more alluring and enjoyable.
Granted, not all tasks bring us joy, but a shift in perspective can definitely help, and sometimes it’s necessary to bring clarity.
Why does this matter?
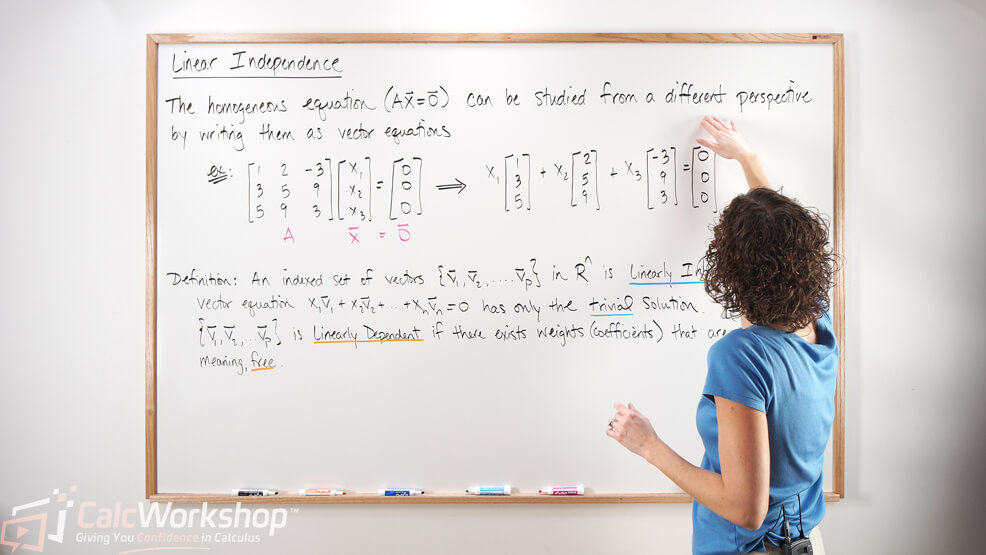
Applying Perspective Shift to Linear Independence
Because when we shift our perspective from a linear system to vector equations, our focus shifts from the unknown solution to the vectors that appear.
And this is important because, for homogeneous equations, when we focus on the vectors that appear in the equation, we can quickly determine whether or not the system contains the trivial solution.
If you recall, a homogeneous system, \(A \vec{x}=\overrightarrow{0}\), of linear equations is when the system has only one solution (i.e., the trivial solution which is the zero vector) or the system has more than one solution.
And the trivial solution is the zero-vector solution, whereas a non-trivial solution is any solution other than the trivial one.
But why do we care?
Because if we can determine that the trivial solution is the one solution for the vector equation, then the system is linearly independent!
Alright, so let’s talk about linear independence!
Defining Linear Independence and Dependence
An indexed set of vectors \(\left\{\overrightarrow{v_{1}}, \ldots, \overrightarrow{v_{p}}\right\}\) in \(\mathbb{R}^{n}\) is said to be linearly independent if the vector equation \(x_{1} \overrightarrow{v_{1}}+x_{2} \overrightarrow{v_{2}}+\ldots+x_{p} \overrightarrow{v_{p}}=\overrightarrow{0}\) has only the trivial solution. And a set of vectors is said to be linearly dependent if there exist weights \(c_{1}, \ldots, c_{p}\), not all zero, such that \(c_{1} \overrightarrow{v_{1}}+c_{2} \overrightarrow{v_{2}}+\ldots+c_{p} \overrightarrow{v_{p}}=\overrightarrow{0}\)
Let’s look at an example to help makes sense of this.
Examples and Applications of Linear Independence
Suppose we want to determine whether the following vectors are linearly independent or linearly dependent.
\begin{aligned}
\overrightarrow{v_{1}} & =\left[\begin{array}{c}3 \\ 2 \\ -4\end{array}\right] \\
\overrightarrow{v_{2}} & =\left[\begin{array}{c}-6 \\ 1 \\ 7\end{array}\right] \\
\overrightarrow{v_{3}} & =\left[\begin{array}{c}0 \\ -5 \\ 2\end{array}\right]
\end{aligned}
We must determine if there is a unique, trivial solution or if there is a non-trivial solution to the system (i.e., free variables). We do this by augmenting the matrix with the zero vector and row reducing.
\begin{aligned}
\left[\begin{array}{cccc}
3 & -6 & 0 & 0 \\
2 & 1 & -5 & 0 \\
-4 & 7 & 2 & 0
\end{array}\right] & \sim\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0
\end{array}\right]
\end{aligned}
Notice that \(x_{1}=0, x_{2}=0\), and \(x_{3}=0\), which is the trivial solution. So, \(\overrightarrow{v_{1}}, \overrightarrow{v_{2}}, \overrightarrow{v_{3}}\) are linearly independent!
Cool, right?
And the process of linear independence can be applied to matrix columns as well.
Determining Linear Independence in Matrix Columns
Suppose we are given a matrix \(A=\left[\begin{array}{lll}\overrightarrow{a_{1}} & \cdots & \overrightarrow{a_{n}}\end{array}\right]\) instead of a set of vectors. Well, the matrix equation \(A \vec{x}=\overrightarrow{0}\) can always be written as \(x_{1} \overrightarrow{a_{1}}+x_{2} \overrightarrow{a_{2}}+\cdots+x_{n} \overrightarrow{a_{n}}=\overrightarrow{0}\). So that means that the columns of matrix A are linearly independent if and only if the equation has only the trivial solution.
Okay, so let’s determine if the columns of the following matrix are linearly independent.
\begin{align*}
A=\left[\begin{array}{lll}
1 & 4 & 2 \\
2 & 5 & 1 \\
3 & 6 & 0
\end{array}\right]
\end{align*}
First, we will augment our matrix with the zero vector and row reduce.
\begin{align*}
\left[\begin{array}{llll}
1 & 4 & 2 & 0 \\
2 & 5 & 1 & 0 \\
3 & 6 & 0 & 0
\end{array}\right] \sim\left[\begin{array}{cccc}
1 & 0 & -2 & 0 \\
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0
\end{array}\right]
\end{align*}
Next, we will recognize that there are two pivots, or basic variables, namely \(x_{1}\) and \(x_{2}\), and one free variable, \(x_{3}\). Consequently, the solution is non-trivial because there is a free variable, and the columns of A are linearly dependent.
And here’s something pretty cool… a set of two vectors \(\left\{\overrightarrow{v_{1}}, \overrightarrow{v_{2}}\right\}\) is linearly dependent if at least one of the vectors is a multiple of the other. The set is linearly independent if and only if neither of the vectors is a multiple of each other.
For example, \(\overrightarrow{v_{1}}=\left[\begin{array}{l}1 \\ 3\end{array}\right], \overrightarrow{v_{2}}=\left[\begin{array}{l}2 \\ 6\end{array}\right]\) are linearly dependent because \(2 \overrightarrow{v_{1}}=\overrightarrow{v_{2}}\), as \(\overrightarrow{v_{1}}\) is a multiple of \(\overrightarrow{v_{2}}\) by a scale of 2
However, \(\overrightarrow{v_{1}}=\left[\begin{array}{l}1 \\ 3\end{array}\right], \overrightarrow{v_{2}}=\left[\begin{array}{l}6 \\ 2\end{array}\right]\) are linearly independent as \(\overrightarrow{v_{1}}\) is a not a scalar multiple of \(\overrightarrow{v_{2}}\).
But what if a set contains more than just two vectors? What do we do then?
Well, we create an augmented matrix with the zero vector and determine if we get the trivial solution (all zeroes) or non-trivial solution (free variables).
Additionally, it may help to note that if a set contains the zero vector, the set is automatically linearly independent.
Moreover, if a set contains more vectors than entries in each vector, the set will automatically be linearly dependent.
\begin{equation}
n\left[\begin{array}{lllll}
* & * & * & * & * \\
* & * & * & * & * \\
* & * & * & * & *
\end{array}\right]
\end{equation}
As the matrix above indicates, the columns are linearly dependent since \(p>n\). In other words, there are more columns than rows.
Together, we will learn all about linear independence and dependence for sets of vectors and matrix columns and the skills needed to characterize linearly dependent sets.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.