How to use the squeeze theorem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s exactly what you’re going to learn in today’s calculus class.
Let’s go!
Did you know that any function squeezed between two other functions at a particular point will then get pinched to that same point?
In fact, that’s the whole idea behind the squeeze theorem, also known as the pinching theorem or the sandwich theorem.
What Is The Squeeze Theorem
Now, from our previous lessons dealing with evaluating limits, we have learned that certain oscillating functions are considered discontinuous or undefined at the point of oscillation. Therefore we are unable to determine the limit of such functions.
But with the help of the squeeze theorem, we can now determine the limit of an oscillating function!
All we have to do is conform, or squeeze, the oscillating curve between two other known functions whose limits are known and easy to compute. In other words, the squeeze theorem is a proof that shows the value of a limit by smooshing a tricky function between two equal and known values.
Think of it this way — imagine you’re hungry, and you decide to make a Peanut-Butter Sandwich (substitute the peanut-butter for your spread of choice).
So, you acquire the necessary ingredients: peanut-butter and two pieces of bread, and you slather the peanut-butter onto one slice of bread (or if you’re like me, on both), then press the two slices of bread together.
Viola!
The peanut-butter is trapped or sandwiched between the two pieces of bread, which means the stickiness (trickiness) is contained.
And that’s what we’re going to do with the Squeeze or Sandwich Theorem. We’re going to squeeze the tricky function between two easy ones!
The Squeeze Theorem states,
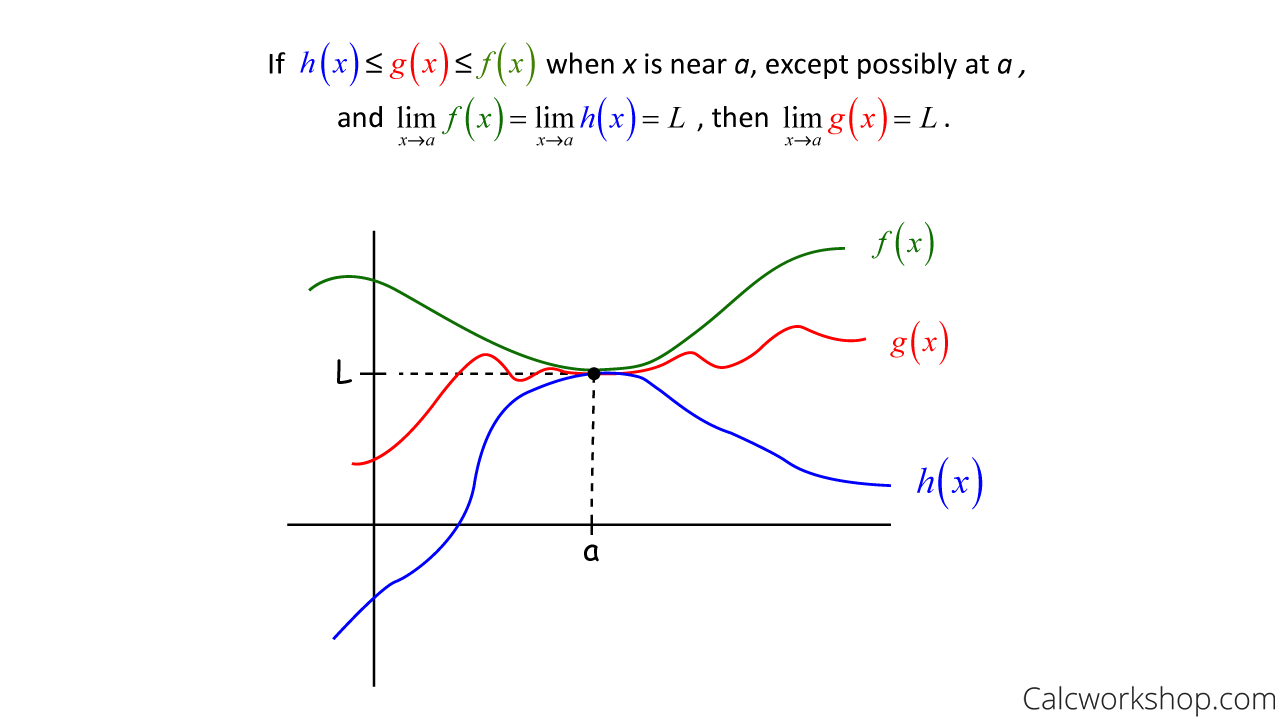
What Is The Squeeze Theorem
All this says is that if g(x) is squeezed between f(x) and h(x) near a, and if f(x) and h(x) have the same limit L at a, then g(x) is trapped and will be forced to have the same limit L at a also.
Example
Let’s look at a classic example of the squeeze theorem in action.
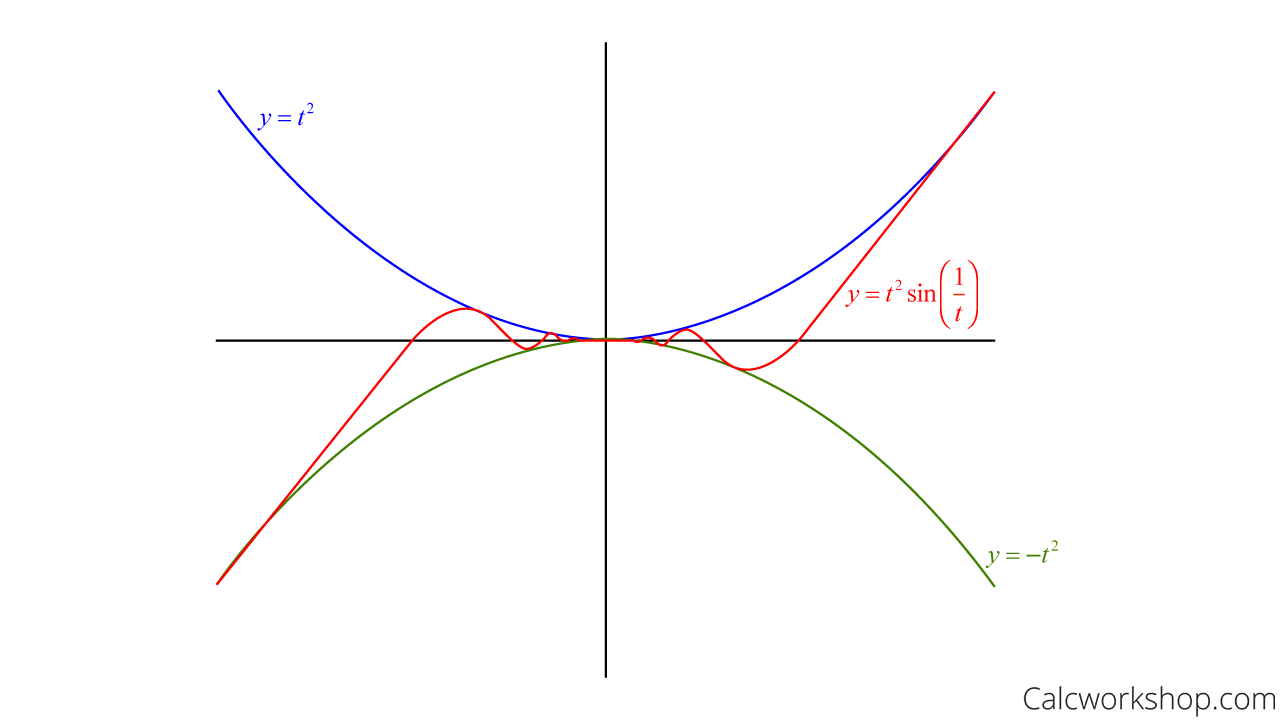
Sandwich Theorem — Sin Function
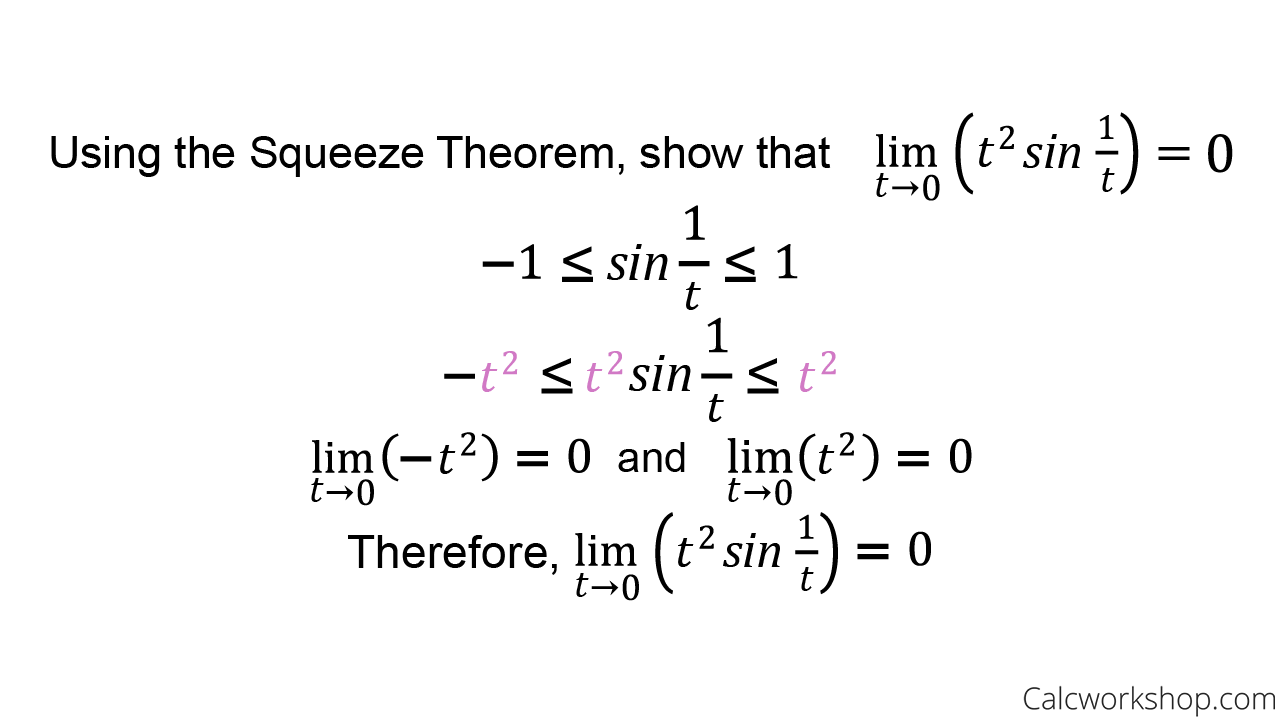
Example of the Sandwich Theorem
Well, guess what, you just did the Squeeze Theorem! We were able to determine that our oscillating function has a limit of zero.
Math is delicious, isn’t it!
Is Squeeze Theorem Always Zero
Together we will look at how to apply the squeeze theorem for some unwieldy functions and successfully determine their limit values.
I want to point out that we tend to use the squeeze theorem for oscillating sine or cosine curves. And therefore, you will find that many of the answers will be zero because the origin is an easy place for us to pinch the oscillation using other known functions.
But there are instances when the squeeze theorem will yield an answer other than zero.
Example
For instance, imagine you have 3x < f(x) < x^3 + 2 , where 0 < x < 2. And you want to evaluate the limit as x approaches 1 of f(x).
And you want to evaluate the limit as x approaches 1 of f(x).

Squeeze Theorem Examples — Not Zero
Now, you may be asking why we need the Squeeze Theorem when we have our Rules for Indeterminate Forms?
Great question!
Well, in accordance with UC Davis, the Squeeze Principle is used on limit problems where the usual algebraic methods, such as factoring, common denominators, conjugation, or other algebraic manipulation are not effective.
Together we will see how to use and verify the Squeeze Theorem to evaluate a limit by walking through four examples, set-by-step.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.