When you see the word “indeterminate,” you instantly think of something that is unknown or cannot be determined.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Are Indeterminate Forms
When applying Limit Rules, we will occasionally encounter values that are not definite.
Meaning, it just won’t work when substituting a value into our function.
Such limits are called indeterminate forms, and this lesson is all about how to handle those prickly problems.
Formally, an indeterminate form is when you evaluate a limit function, and you get one of the following values:

7 Indeterminate Forms
We will focus solely on the first two indeterminate forms of zero divided by zero or infinity divided by infinity, as they are the most common types of indeterminate expressions and save the rest for L’Hopital’s rule, sometimes spelled L’Hospital, which utilized derivatives.
Continuity Vs Discontinuity
Okay, let’s quickly recall our discussion of continuity and discontinuity from our previous lesson of finding limits graphically.
A function is continuous if and only if you can draw the graph without ever picking up your pencil. Otherwise, the function is discontinuous. And there are four types of discontinuities:
- Point
- Infinite
- Jump
- Oscillating
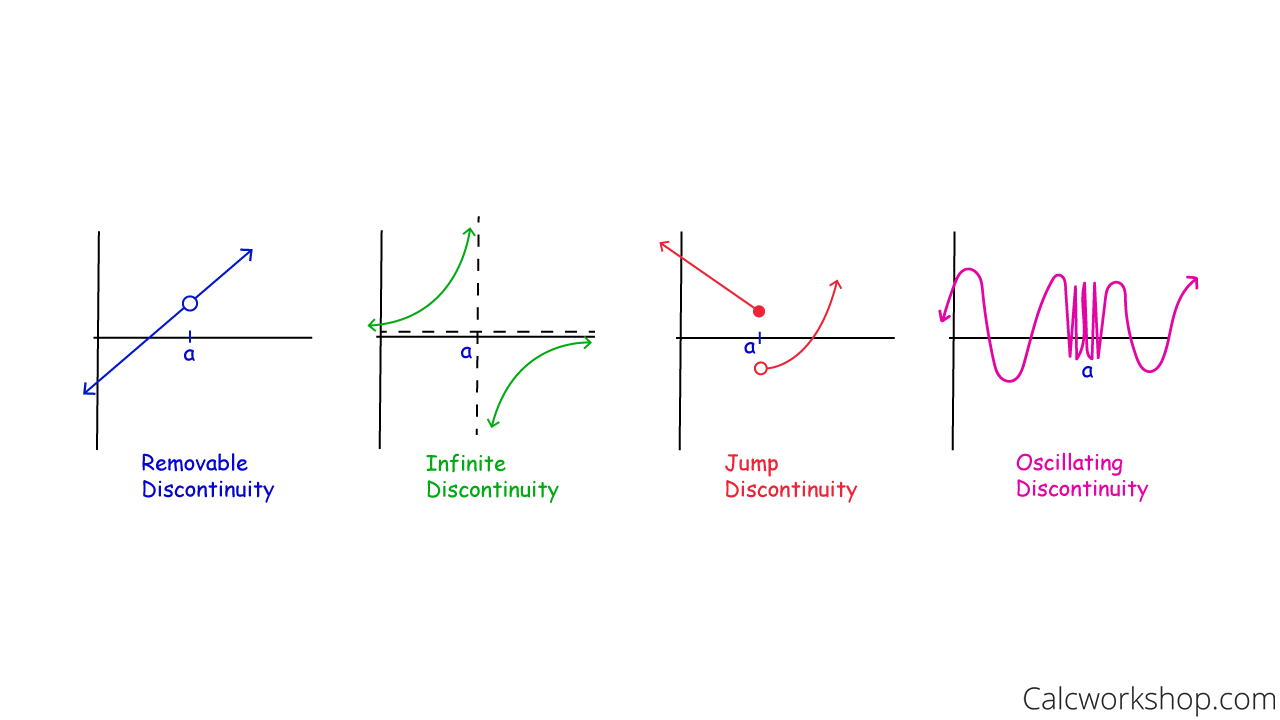
4 Types Of Discontinuity
But here’s the most fascinating thing about limits. Just because the function is discontinuous doesn’t necessarily mean that we can’t determine what it’s approaching!
Example – Using Graphs
For example, suppose you are asked to find the following limit.

Zero Divided By Zero — Indeterminate
Hmm, when we plug in our given value, we get zero over zero, which is indeterminate. Does this mean the limit does not exist?
Not at all!
A quick look at the graph confirms that we are dealing with removable discontinuity (point or hole discontinuity) and that while the function is undefined at x = 3, we can still approach from both the left and right.

Removable Discontinuity — Graph
Which means the limit is 6.
Okay, but does this mean that we have to graph the function every time we encounter an indeterminate form and then evaluate the limit graphically?
Because that seems tedious…
Thankfully, no.
With the power of one-sided limits and some pretty cool tricks, we will be able to simplify the function and arrive at the necessary answer without having to graph — but graphing is a fantastic method, so feel free to use it from time to time!
How To Solve Indeterminate Forms
Tricks? What kind of tricks?
We evaluate indeterminate forms by:
- Factoring
- Applying Common Denominators
- Using Conjugate Pairs
- Working With Trig Identities
Example – Using Factoring
For example, using our question from above, let’s apply the algebraic method of factoring to help us evaluate the limit.
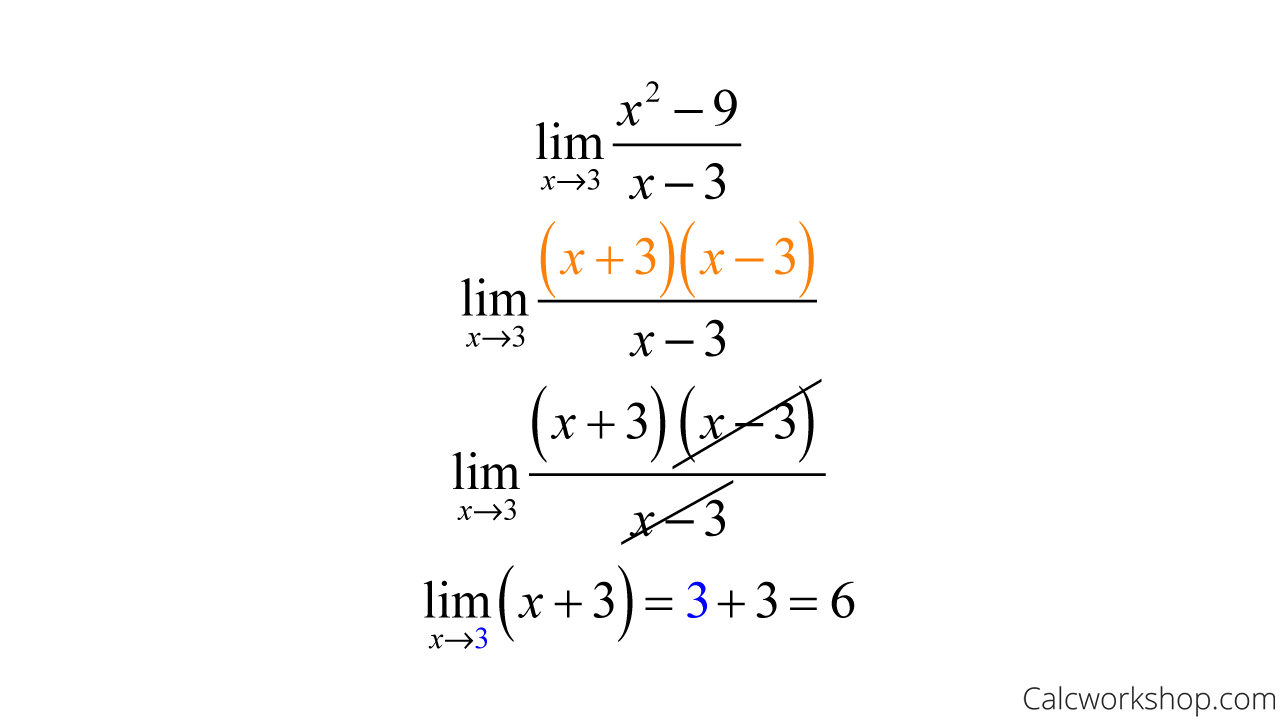
Calculus Indeterminate Forms — Factoring
Example – Using Conjugates
Let’s quickly look at another example. This time we will employ the method of conjugates.
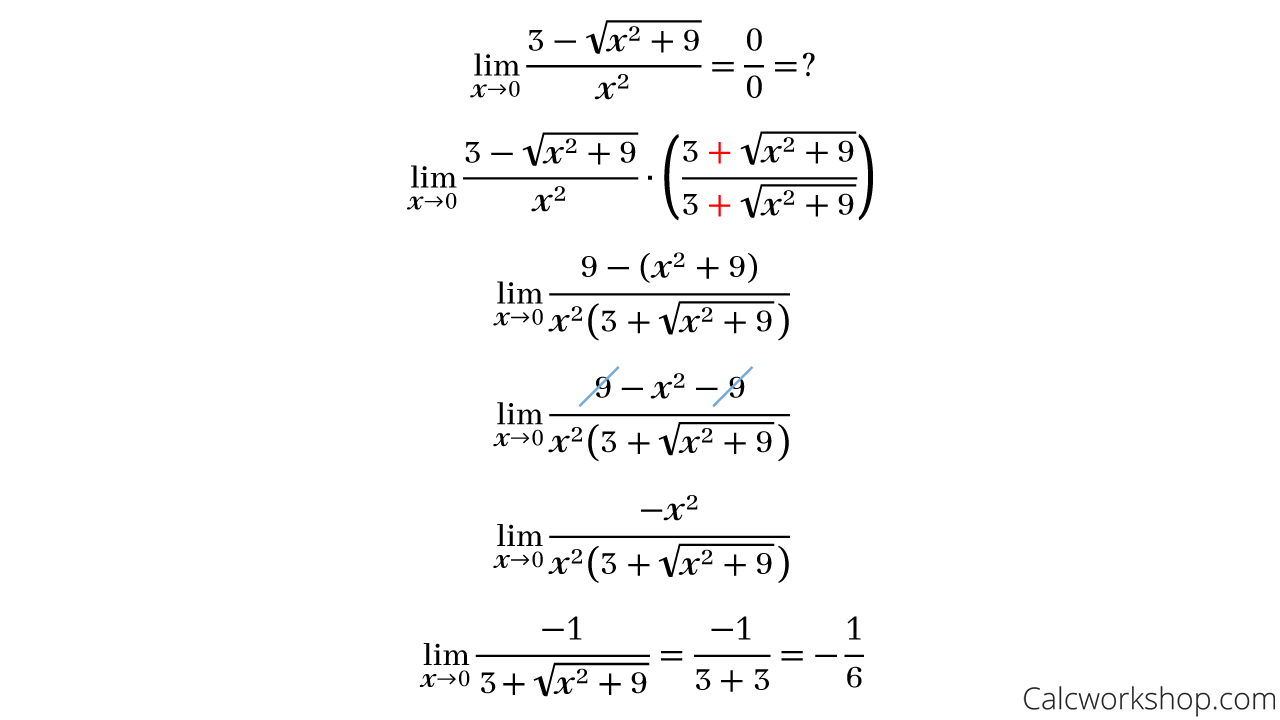
Using the Conjugate to Evaluate a Limit
Summary
So, the key to evaluating limits of indeterminate form is to employ our four algebraic techniques.
It is worth mentioning that some textbooks may refer to these techniques as factorization (fraction reduction), rationalization, and Trigonometric rules, as does Khan Academy.
What’s important is that the techniques are all the same, no matter what it is called.
Together we will walk through countless examples, step-by-step, in order to see the power of factoring, common denominators, conjugate math, and some pretty awesome trigonometric rules as they help us find the solutions we desire.
In fact, I consider this video lesson one of the most critical lessons in our limits chapter because the skills and techniques we learn in this video will enable us to find derivatives and integrals later in our calculus course.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.