Is it possible to determine what is happening to a function if we let x get really large or small?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In other words, what’s the limit at infinity?
What Is Infinity
First, we need to understand that infinity is not a tangible value but an idea.
It is used to represent a number that is greater than any real number.
Largely (pun intended), infinity is used to explain the end behavior of a function that is either increasing or decreasing without bound.
So, if infinity isn’t actually attainable, how can we approach it?
Convergence (The Main Ingredient)
First, we will need to understand the notion of convergence, which is the idea that the value of a function eventually becomes arbitrarily close to some number.
For example, look at the graph below. As the x-value increases, what is happening to the y-value?
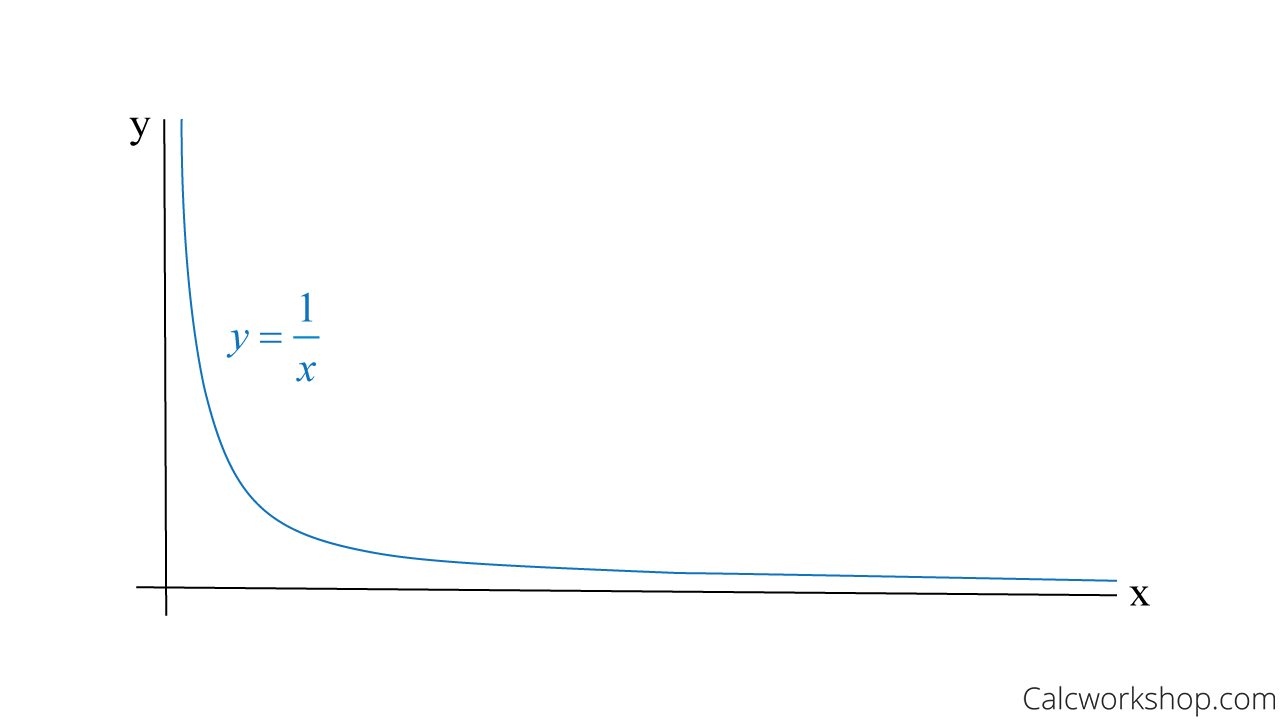
1 Divided by X — Graph
As x gets bigger and bigger (approaching positive infinity), the y-values are getting smaller and smaller (approaching zero).
And that’s the secret to limits at infinity, or as some textbooks say, limits approaching infinity.
All you have to do is find the function’s end-behavior.
Constant Over Infinity
And this brings us to a cool idea — any number divided by a really big number is approximately zero!

Theorem For Limits At Infinity
Example
For instance, let’s apply our new limit rule to evaluate the following limit.

How To Solve Limits At Infinity
See, not so bad!
But here’s the really big question…why does this work?
Horizontal Asymptotes
Because as x gets larger and larger without bound, f(x) gets closer and closer a tangible number. Look back at the graph above of y = 1/x and notice that as x approaches infinity, f(x) approaches zero. This nicely shows that when x approaches infinity the y-value is approaching a horizontal asymptote!
Which means horizontal asymptotes help us to determine the end behavior of a graph and is defined as follows:

Horizontal Asymptote — Definition
Therefore, if we can determine the horizontal asymptote of a function, then we can find the limit at infinity!
Example
In this question, we will evaluate the limit as x approaches infinity by finding the horizontal asymptote algebraically.
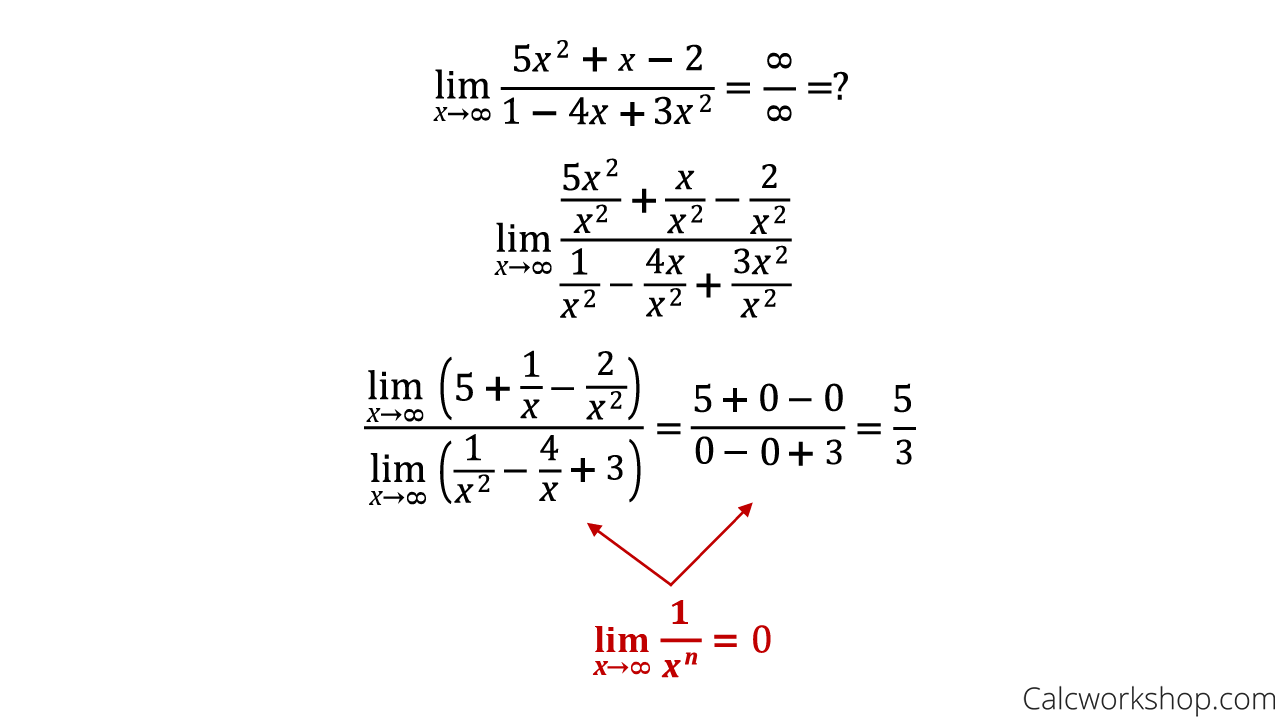
Calculating the Limit at Infinity
Now, I know that you’re probably thinking…
…that seems like a lot of work. And you’re right.
The Shortcut
Thankfully there’s a shortcut to finding horizontal asymptotes and limits at infinity, as the table below nicely highlights.
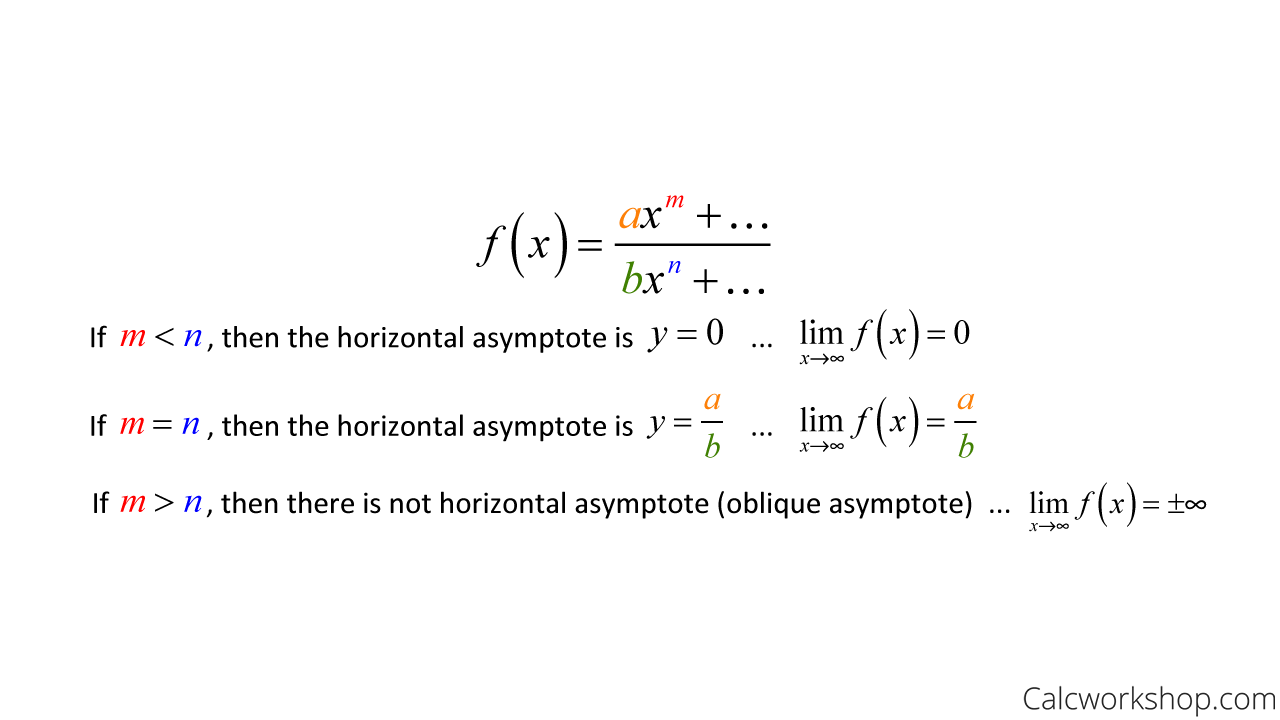
How To Find Horizontal Asymptotes Using Limits
Sweet!
Summary
So, all we have to do is look for the degrees of the numerator and denominator, and we can evaluate limits approaching infinity as Khan Academy nicely confirms.
Together we will look at nine examples, so you’ll know exactly how to handle these questions. In fact, we’re going to utilize this technique countless times throughout our journey of calculus, so get excited!
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.