When you hear the word “limits,” what comes to mind?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
- Speed Limits?
- Credit Limits?
- Physical Limits?
As you can see, limits are all around us!
Well, in this lesson, we’re going to explore the world of “limits” as it pertains to calculus by using a graph because, as the idiom states, a picture is worth a thousand words!
What Is A Limit
If we let f(x) be a function and a and L be real numbers.
Then we say that L is the limit of f(x) as x approaches a, provided that as we get sufficiently close to a, from both sides without actually equaling a, we can make f(x) as close to L.
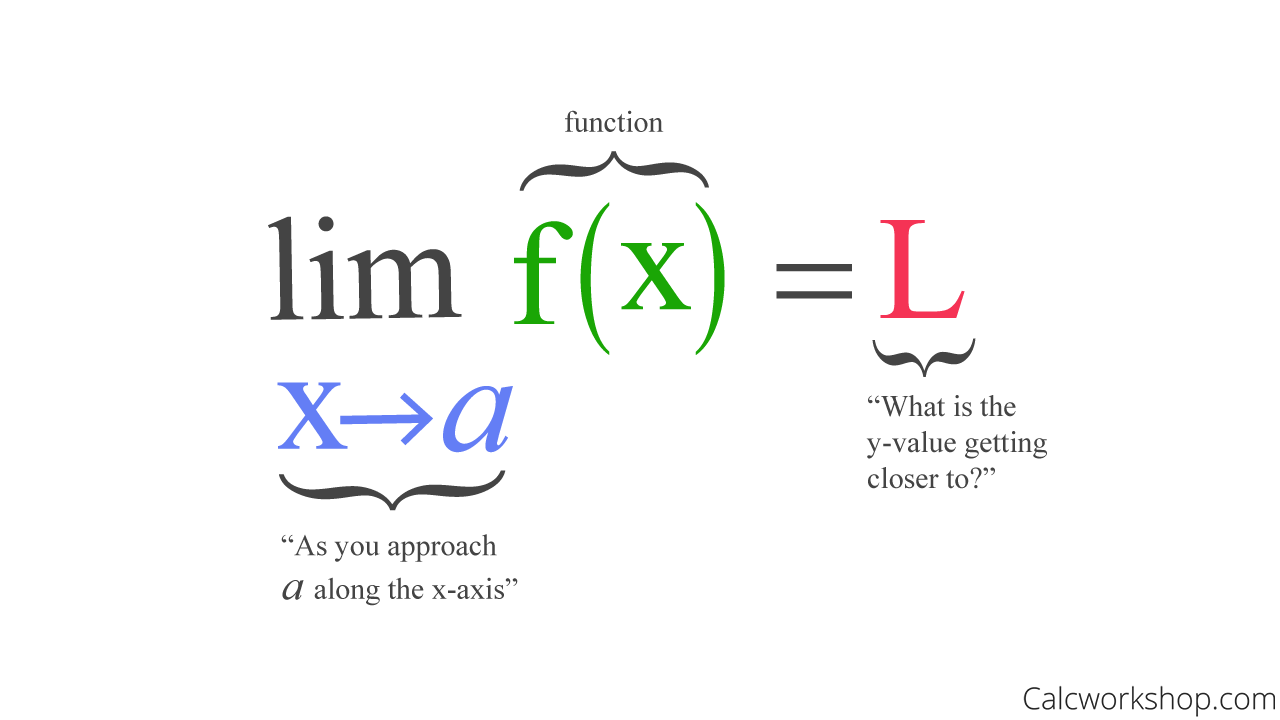
Understanding Limit Notation
Formal definitions can be perplexing at first, so let’s make sense of this.
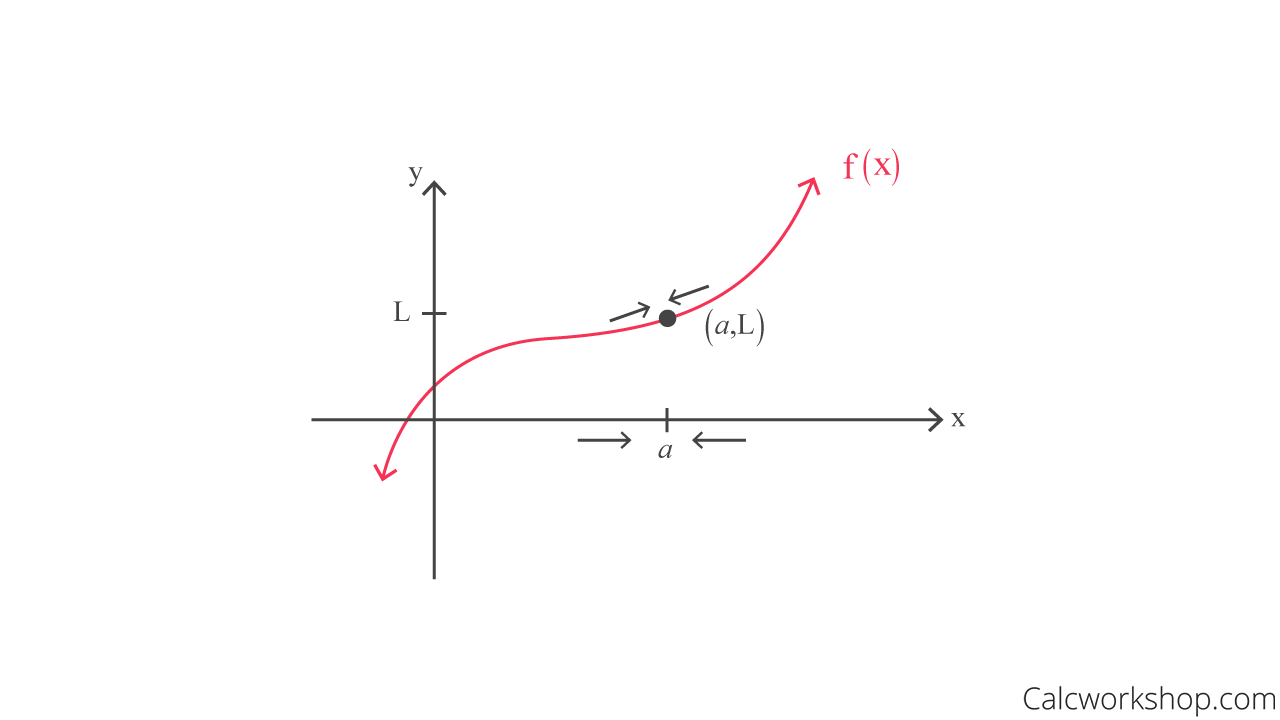
All this definition says is that, as we approach a specific (finite) value along the x-axis from both the left and the right sides, we want to find what the y-value (L) is approaching.
How To Find A Limit On A Graph
That’s it!
One & Two Sided Limits
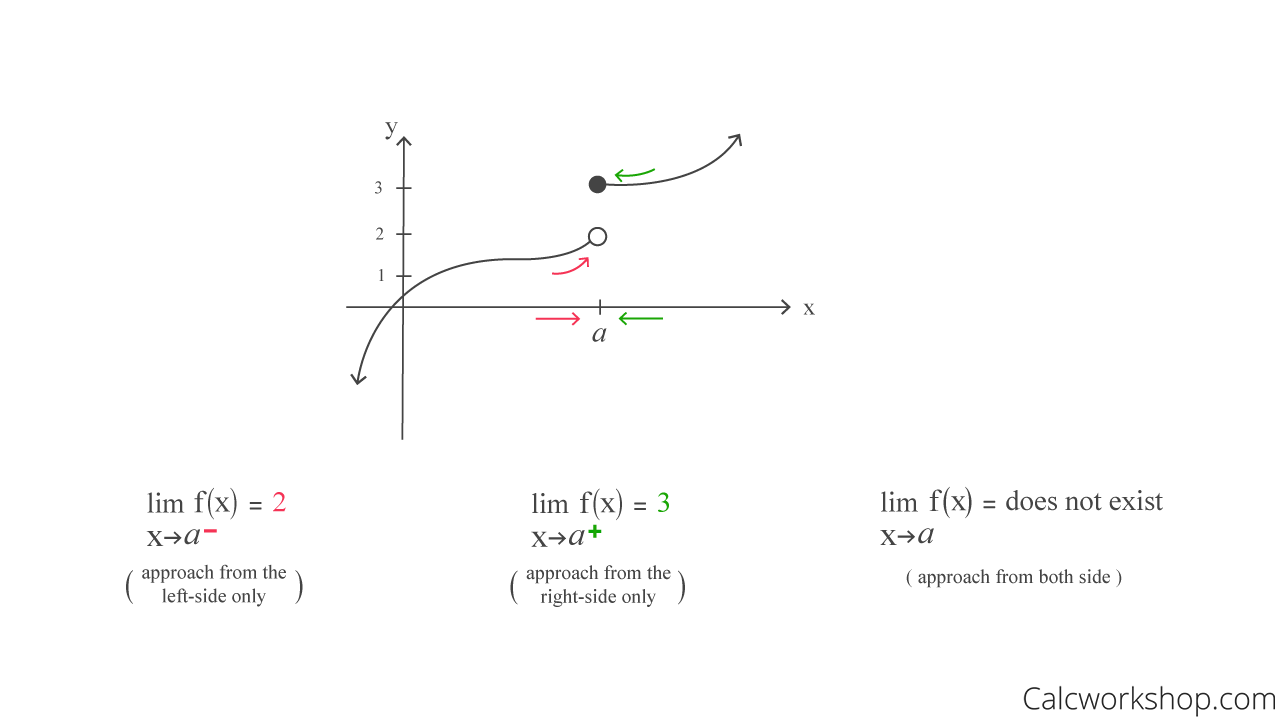
Additionally, did you know that sometimes we are just interested in what’s happening as we approach from only one side, either the right or the left?
This is called a one-sided limit.

One Sided Limits
And what’s so cool is that our formal definition of a limit is called a two-sided limit, as it asks us to approach from both the left and the right.
But what happens if we can’t determine what the y-value is approaching?
If f(x) doesn’t approach a specific finite value as x approaches a from both directions, then we say that the limit does not exist.
Let’s look at an example of how to solve a limit graphically by investigating some one-sided and two-sided limits.
How To Find One Sided Limits
Because the limit (i.e., y-value) gets closer to two different values as we approach a from either side of a, we can’t make up our mind as to what our limit should be….therefore, we say that the limit does not exist.
Consequently, a limit only exists if and only if the limit from the left-side equals the limit from the right-side.

Formal Definition Of A Limit
Furthermore, we will learn how to use one-sided limits for when we wish to find limits approaching infinity!
Continuity
And this brings us to another vital concept — continuity.
Informally, if you can sketch a graph without lifting your pencil off the paper, then we say that function is continuous. Otherwise, we declare a function is discontinuous.
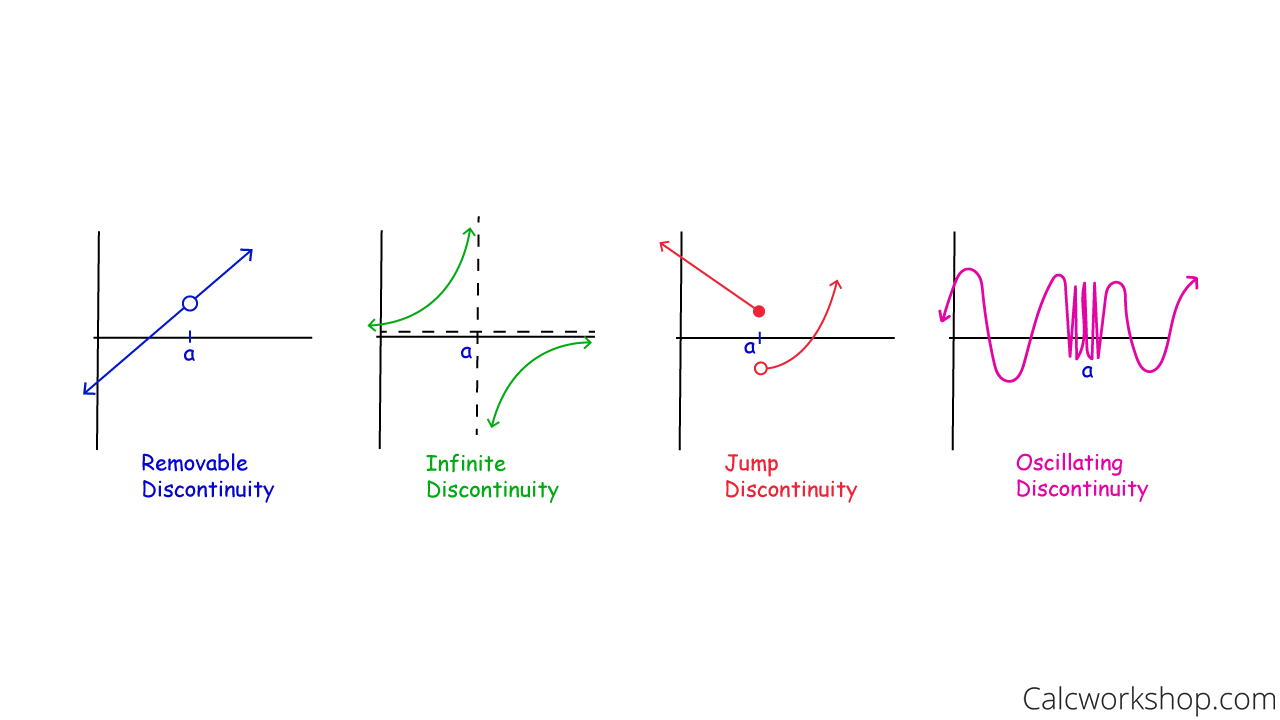
There are four types of discontinuity:
- Removable (Point)
- Infinite (Asymptote)
- Jump
- Oscillating
4 Types Of Discontinuity
But the most incredible thing is that even if a function is discontinuous, it’s still possible to find the limit!
Remember, we only care about what is happening as we approach (get sufficiently close to) the value “a.” In fact, a limit couldn’t care less about what’s actually happening “at” x = a, and therefore even if a function is discontinuous, we are sometimes able to compute limits.
Finding Limits Graphically
For example, let’s find the limits of the following functions graphically.

Evaluating Limits Using A Graph
But why do we care about limits?
Because limits are foundational to understanding calculus, the limit concept distinguishes calculus from all other branches of mathematics in the sense that it declares interest in how things change over time.
Likewise, a limit helps us to understand the idea of closeness and approximation and is the foundation for definitions such as continuity, differentiation, and antidifferentiations (i.e., integrals).
And here’s the best part, this cornerstone topic is easy to understand and master because the crux of what we will do can be summed up with one question.
“As you get closer and closer to a particular value along the x-axis, what is the y-value getting closer and closer to?”
So, together we’re going to look at 29 examples!
These examples cover:
- How To Visualize One-Sided And Two-Sided Limits
- Continuity
- Discontinuity
- How To Approach Infinity From Just One Direction
And with this knowledge, we will have the framework necessary to tackle limits numerically and algebraically and to be able to conceptualize a derivative.
Ah, great things to come!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Finding Limits Graphically
Finding Limits Graphically
- What is a limit? and Limit Notation for One and Two Sided Limits
- 3 Examples of finding limits graphically – one sided limits
- 4 Examples of finding limits graphically – removable discontinuity
- 9 Examples of finding limits graphically – one and two sided limits
- 3 Examples of finding limits going to infinity graphically
- 10 Examples of finding limits graphically – review
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.