Did you know that there is a formal, mathematical definition of limits?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In our lessons so far, we have learned how to evaluate a limit of a function graphically and algebraically using limit laws and properties.
And while these laws and definitions enable us to evaluate limits quickly, they have a tiny flaw — they aren’t precise.
Think about it.
Whenever we read a limit, we use the following words: “approach,” “sufficiently close,” “near to,” etc.
So, is there a way to be accurate in our evaluation of the limit of a function?
There sure is! And that’s what this calculus lesson is all about.
Limit Definition
The formal definition of a limit, which is typically called the Epsilon-Delta Definition for Limits or Delta-Epsilon Proof, defines a limit at a finite point that has a finite value.
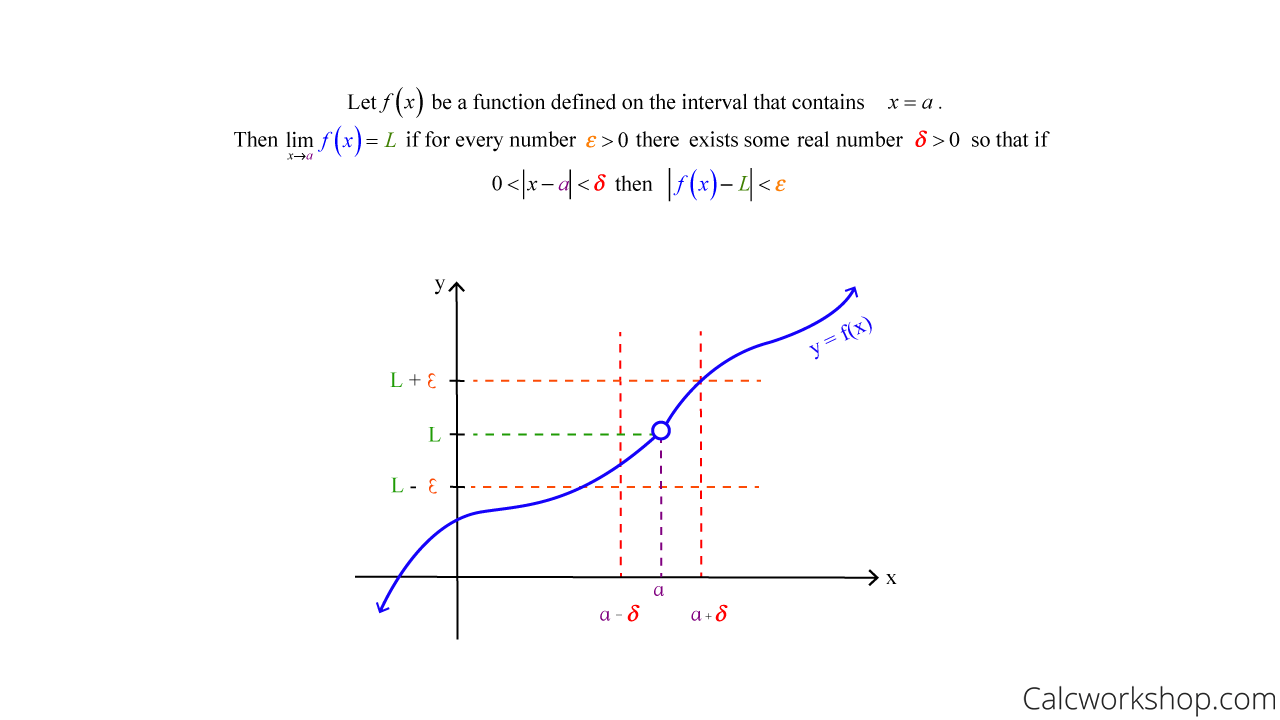
Epsilon Delta Definition Of A Limit
This probably seems completely abstract, doesn’t it?
How To Find Epsilon Delta Definition Of A Limit
Let’s see if we can shine a light on what is happening.
- First, we create two variables, delta (δ) and epsilon (ε).
- Next we choose an epsilon region around the number L on the y-axis.
- Then, we use this region to help us define a delta region around the number a on the x-axis so that all x-values, excluding a, inside the region correspond to y-values inside the epsilon region.
- Finally, we show (prove) that we can find y-values of the function as close as we want to the value L by using only the points in a small enough interval around a.
And as Milefoot Mathematics quickly points out, we will define our limit in such a way as to allow epsilon to represent any number, while we restrict the value of delta; thus, ensuring that our region is precise.
In fact, it’s this restriction on the delta that holds the key to this unique proof!
Let’s look at a few questions to help us make sense of things.
For each of the following, sketch the open interval (a,b) with point c inside. Then find the value of δ > 0 such that a < x < b whenever 0 < | x – c | < δ.
Hint: delta always represents the shortest distance, so it will be your job to determine the shortest distance from either a to c or b to c!
Example #1
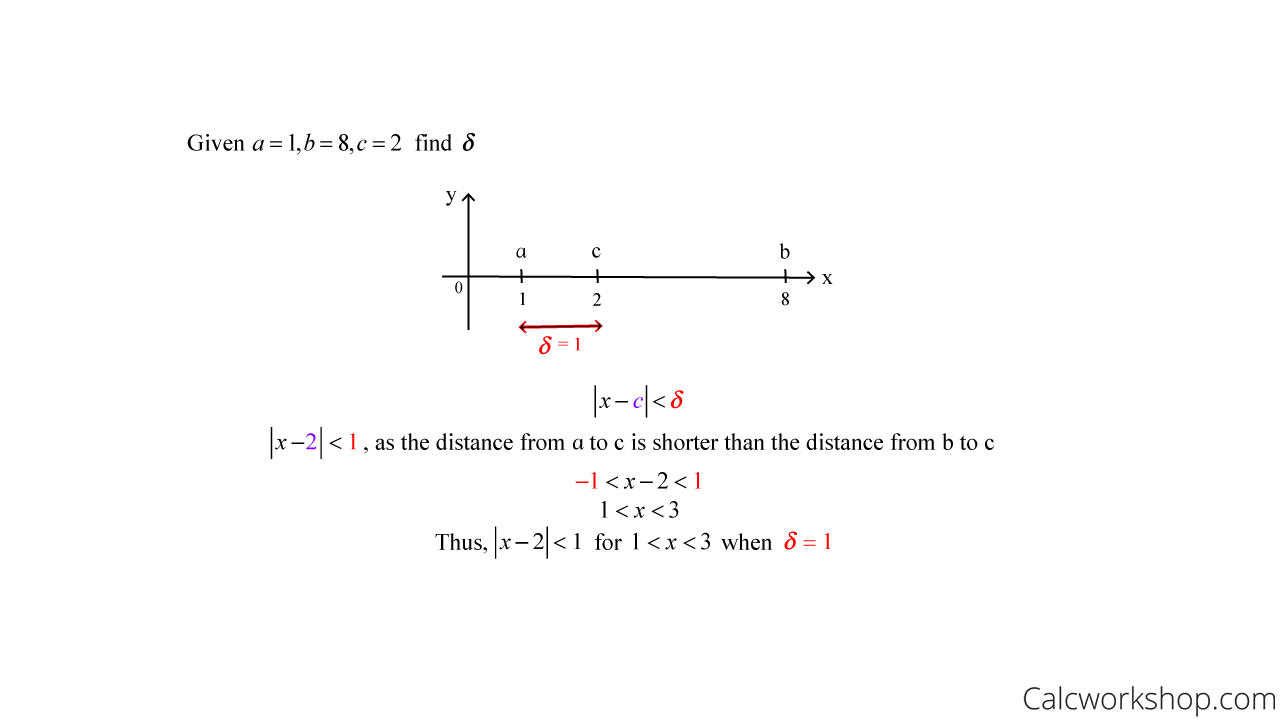
Find Delta Given Epsilon Example 1
Example #2
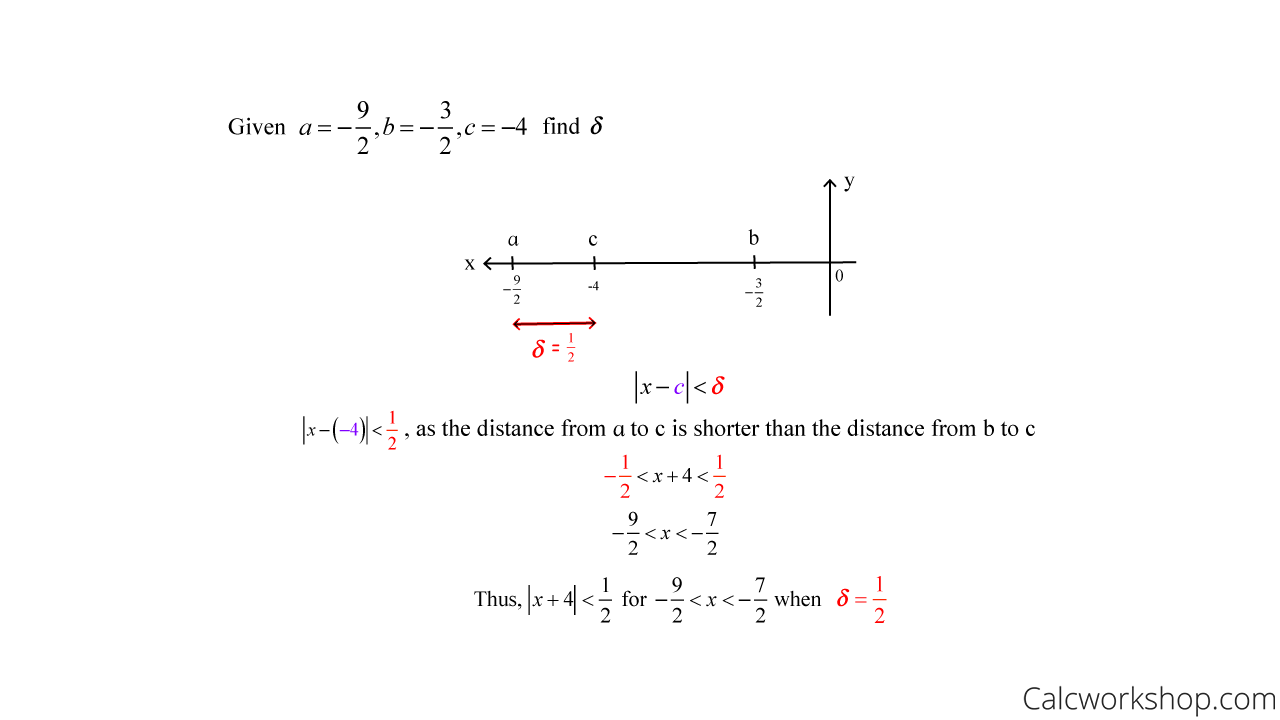
Find Delta Given Epsilon — Example 2
Example #3
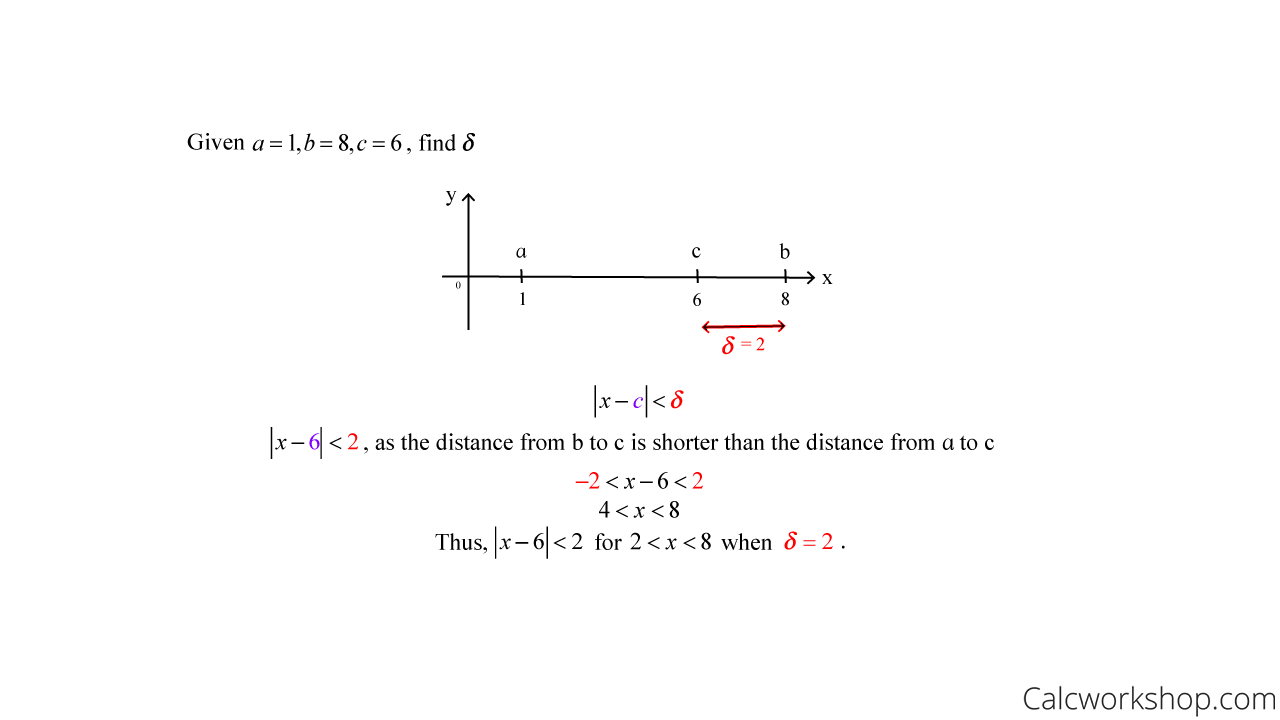
Find Delta Given Epsilon — Example 3
Example #4
Okay, so now that we have a better understanding of what we are looking for in terms of the delta to ensure a precise region, now it’s time to see the formal definition of the limit in action to find epsilon.

Find The Largest Delta That Works For Epsilon
Therefore, the largest value that δ can have is ¼.
Example #5
But what do we do if we aren’t given the value of epsilon?
Then we will leave our answer in terms of epsilon, as seen in the following problem.

Use Epsilon Delta To Prove Limit
Thoughts On The Epsilon Delta Proof
Our video lesson will work through this style of proof in much more detail, and you will see that the proof above is only half complete, as the epsilon-delta proofs are a two-part process.
First, we use the proof to find the value of delta, and then we must “redo” it to prove that our choice of delta is correct. While this may seem tedious, I assure you that it will make sense with a bit of practice.
I will admit that just looking at the proof can seem scary due to all the weird letters and symbols. Still, after seeing it in action and following along with two step-by-step examples of how it is constructed in the video, you will see that this proof is quite straightforward and comes full-circle in the end. Khan Academy even calls it a beautiful proof, and after some practice I think you will see why.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.