Have you ever wondered if there’s a way to simplify the process of solving Laplace transform problems?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Just like how a shortcut helps you reach your destination faster, Laplace transform translation theorems can save you time and effort when dealing with complex integration tasks.
So, let’s see how they work.
First Translation Theorem (First Shifting Theorem)
Our first theorem is called the first translation theorem or shifting theorem.
If
Example: Applying the First Translation Theorem
For instance, let’s evaluate
First, we rewrite using our new symbolism to be
Then we apply our Laplace transform for
Finally, we “shift” our s to s-a and obtain our answer
Easy!
Don’t worry. Together we will learn how to use the first translation theorem and apply the inverse form using partial fractions.
Unit Step Function (Heaviside Function)
Our next translation is on the t-axis, called the unit step function or the Heaviside function, named after the mathematician Oliver Heaviside.
It is aptly named a unit step function because we deal heavily with binary numbers in engineering and computer science.
In other words, we establish a function that takes on the value of 0 (off) or 1 (on) over a time
The unit step function is defined by
. Where
is a function of time , and has 0 for all negative values of before we “flip the switch” and 1 for all positive values of .
Shifted Unit Step Function
Now, in many circuits, a function may be shifted or delayed. Thus, a shifted unit step function is a function that has value 0 up to
Example: Shifted Unit Step Function in Action
Let’s see this in action to really make sense of what is going on.
Express the function in terms of a shifted unit step function and graph the piecewise defined if
Well, this means that our equation
Then our graph for the piecewise function is.

Now let’s take the example above and multiply it by a function
Express the function in terms of a shifted unit step function and graph the piecewise defined if
This means the 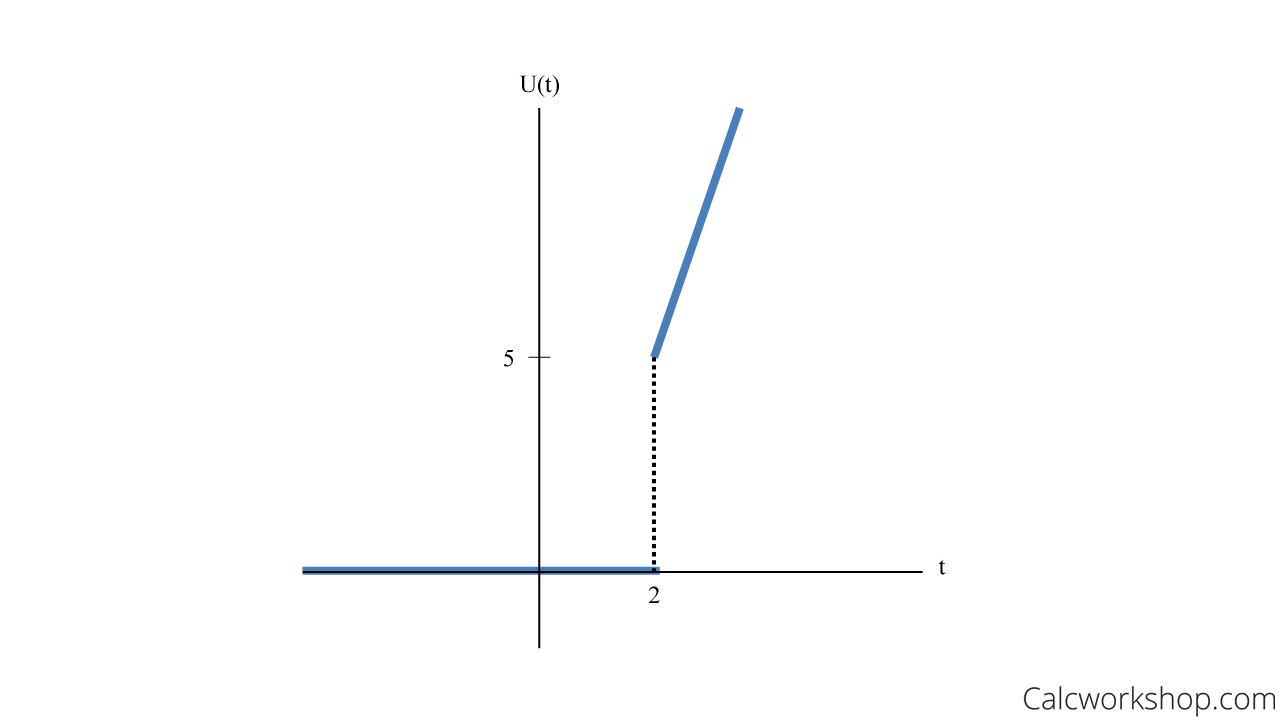
Second Translation Theorem (Second Shifting Theorem)
And this leads us to the second translation theorem, sometimes called the second shifting theorem, where an exponential multiple of
If
But what does this really mean?
We can find the Laplace transform of the function
Example: Applying the Second Translation Theorem
Let’s look at an example.
Suppose we want to find the Laplace transform of the function
First, we apply the Laplace transform to both sides as follows.
Next, we will use our operations properties to separate terms.
Now, all we have to do is apply the transform for each term.
Time-Shift and Frequency-Shift Properties
It’s important to note that these translation theorems allow us to easily switch or step back and forth between time and frequency. In particular, that is why the second translation theorem is sometimes called the Time-Shift Property, and its inverse is called the Frequency-Shift Property.
Next Steps
In the video you’ll
- Acquire the knowledge to work with inverse Laplace transforms, making it easier for you to shift between frequency and time domains when necessary.
- Learn how to apply both the first and second shift theorems to solve complex Laplace transform problems with ease.
- Sharpen your skills and boost your confidence in tackling a wide variety of Laplace transform problems through the video’s step-by-step examples.
Let’s go!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.