Wouldn’t it be nice to have properties that can simplify our calculations of means and variances of random variables?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Thankfully, we do! Linear Combinations is the answer!
More importantly, these properties will allow us to deal with expectations (mean) and variances in terms of other parameters and are valid for both discrete and continuous random variables.
Let’s quickly review a theorem that helps to set the stage for the remaining properties. When we first discussed how to transform and combine discrete random variables, we learned that if you add or subtract a constant to each observation, then you add or subtract that constant to the measures of center (i.e., expectation) but not the spread (i.e., standard deviation). So if a and b are constants, then:
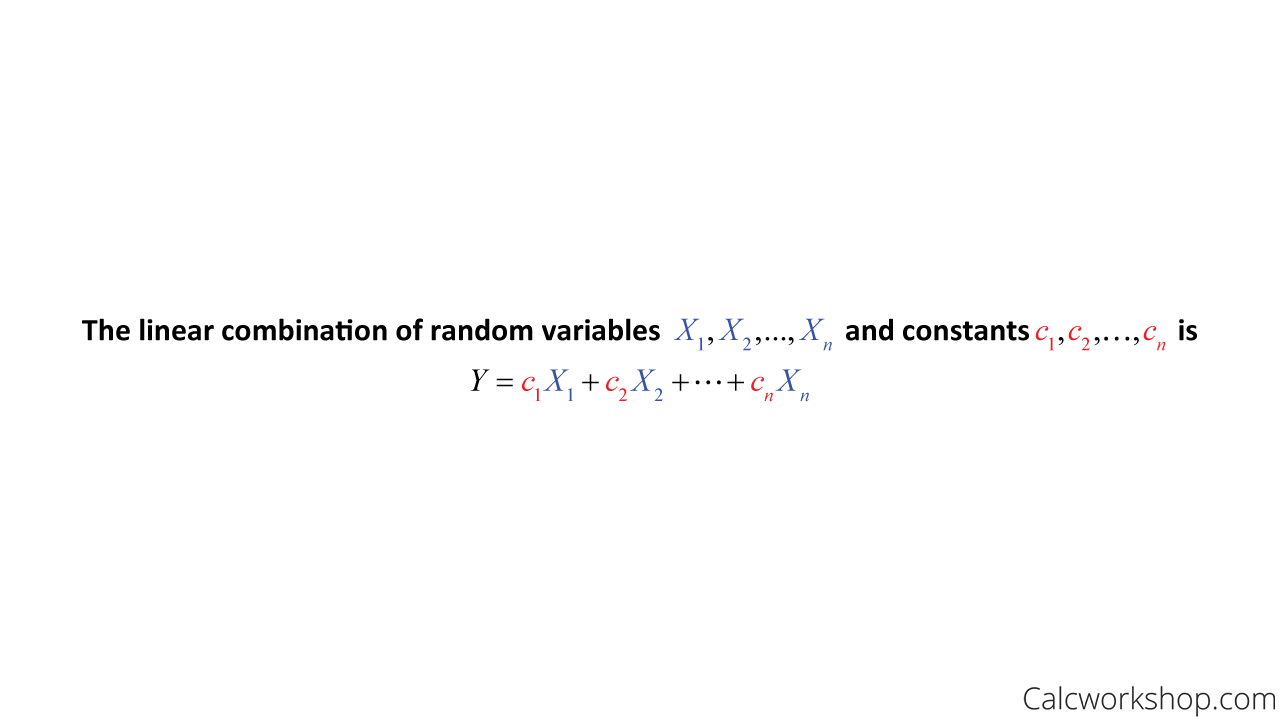
Linear Combination Of Random Variables Defined
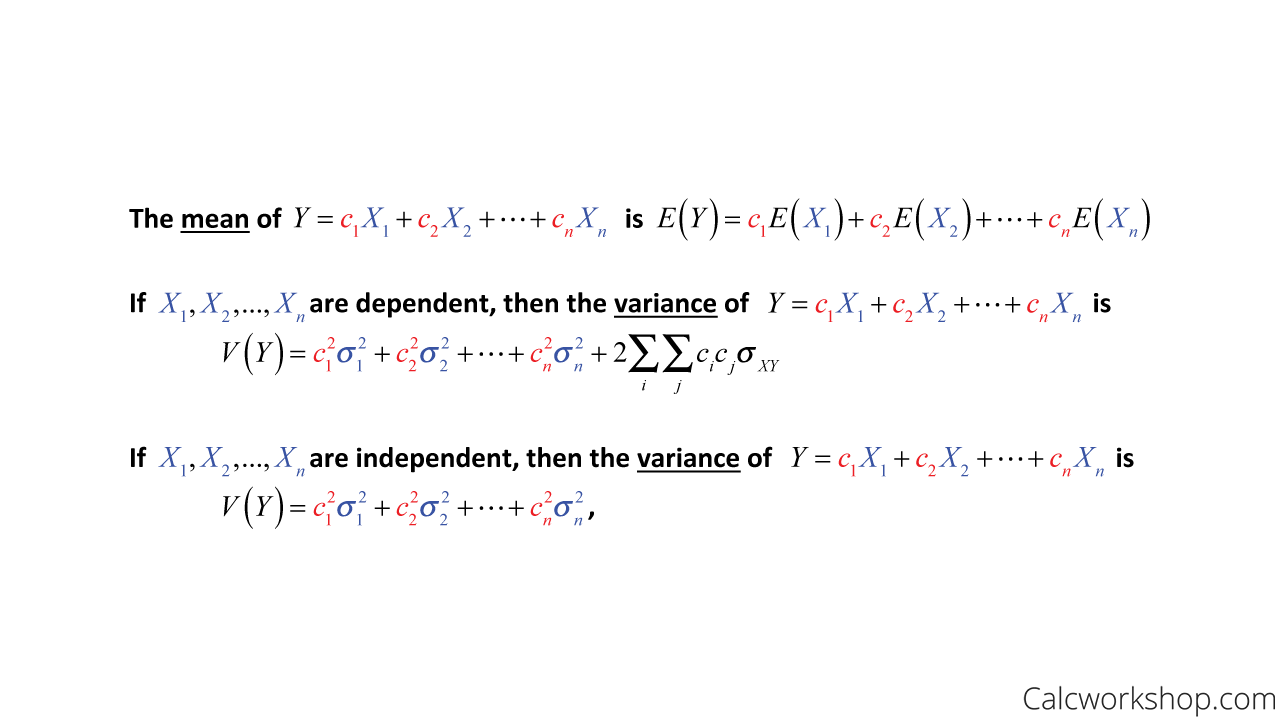
Mean And Variance Of Linear Transformation
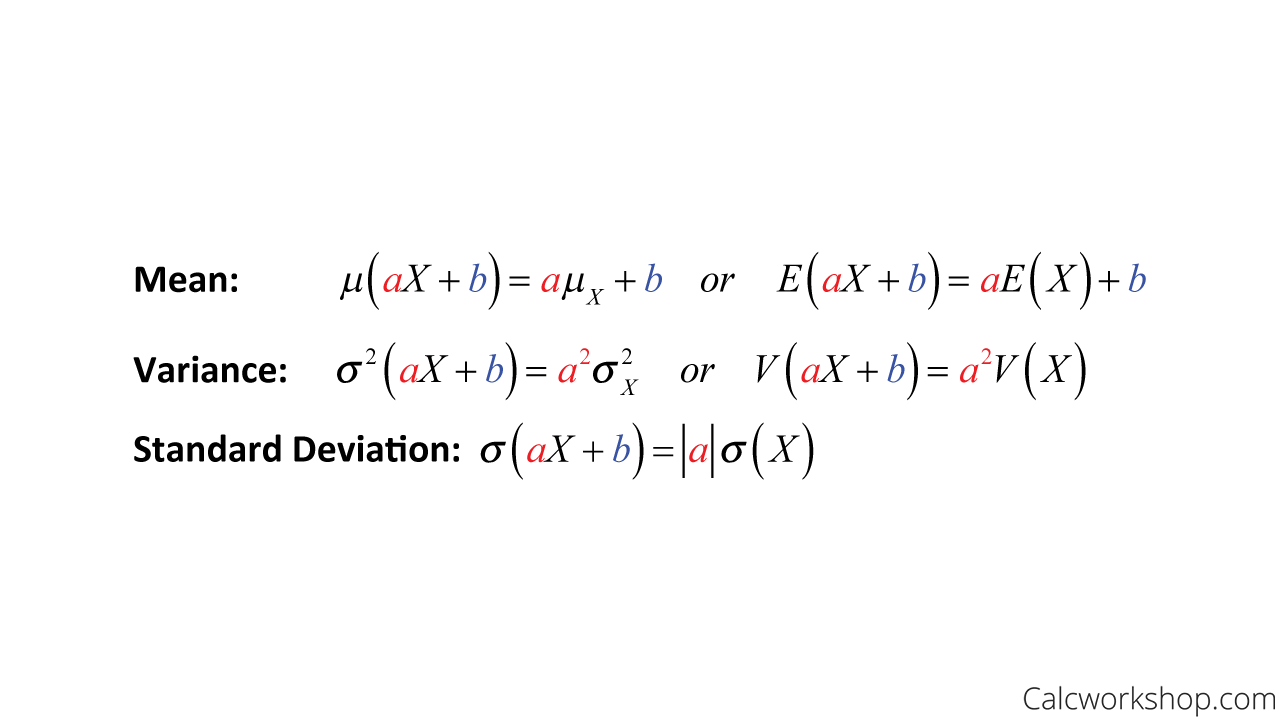
Mean And Variance Formulas
For example, let’s suppose we are given the following probability density function, and we wish to find the expectancy of the continuous random variable.

Mean Transformation For Discrete
Using this very property, we can extend our understanding to finding the expected value and variance of the sum or difference of two or more functions of a random variable X, as shown in the following properties.
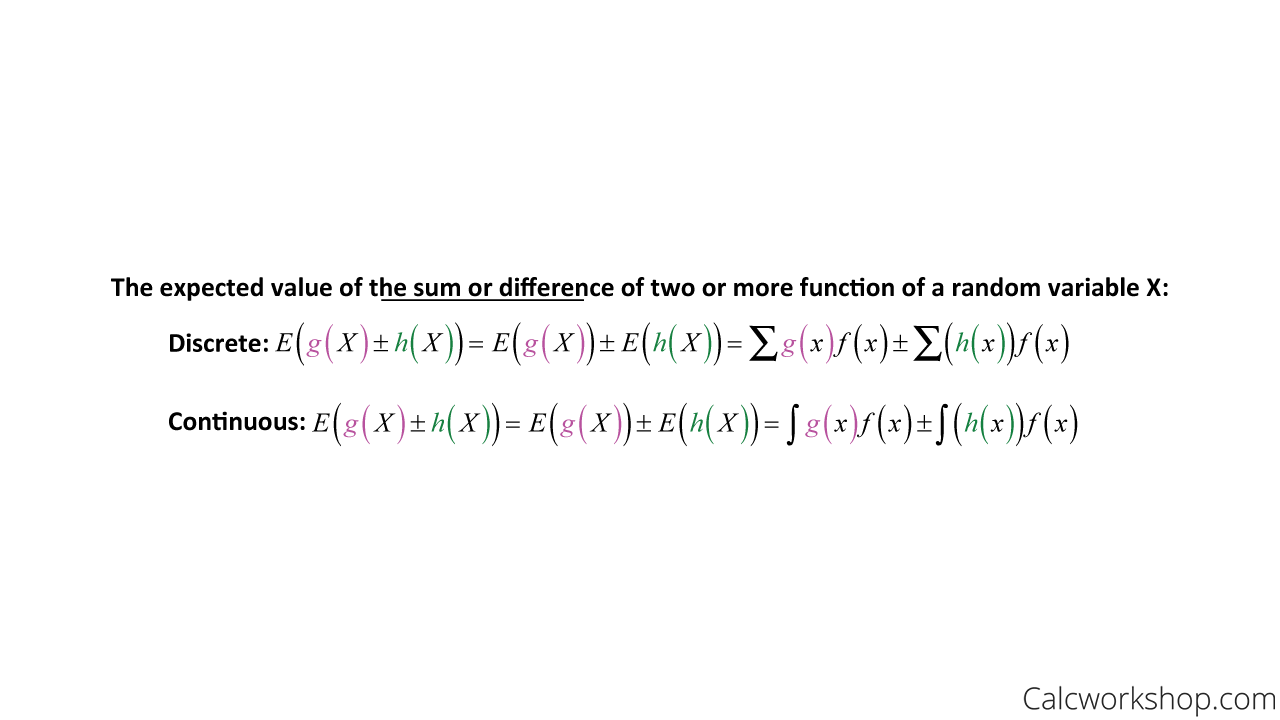
Mean Sum and Difference of Two Random Variables
For example, if we let X be a random variable with the probability distribution shown below, we can find the linear combination’s expected value as follows:
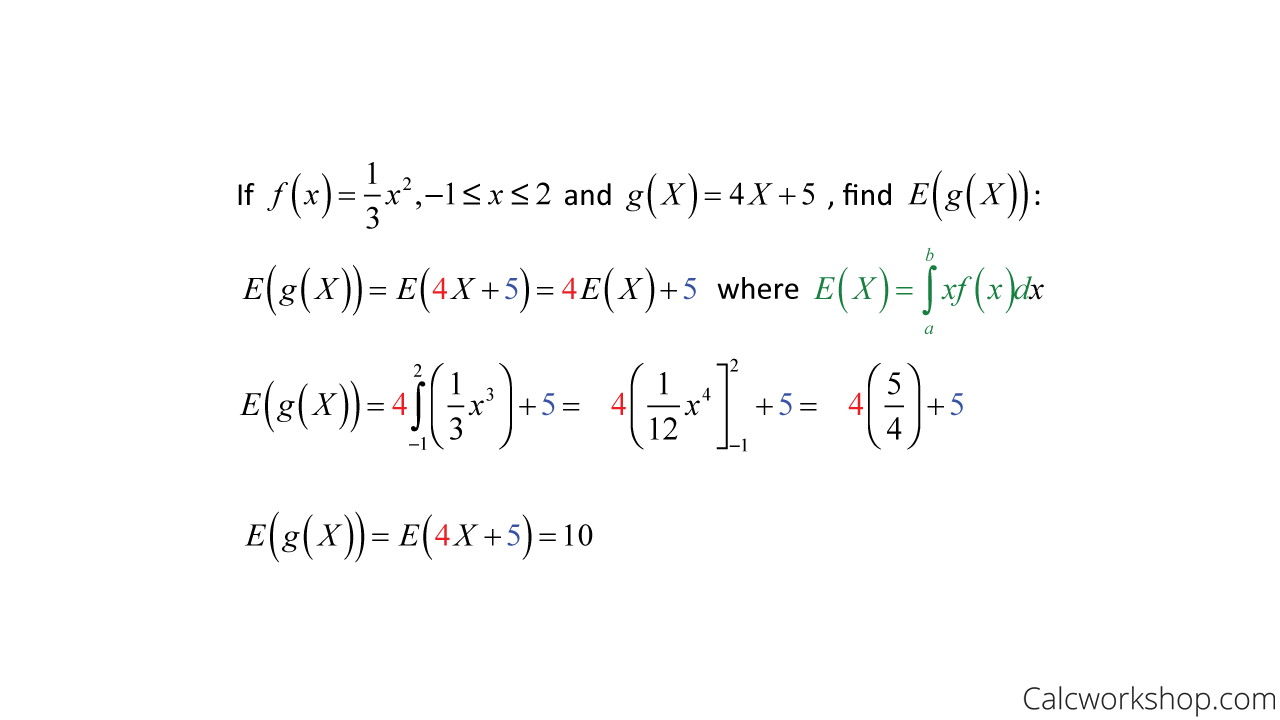
Mean Transformation For Continuous
Additionally, this theorem can be applied to finding the expected value and variance of the sum or difference of two or more functions of the random variables X and Y
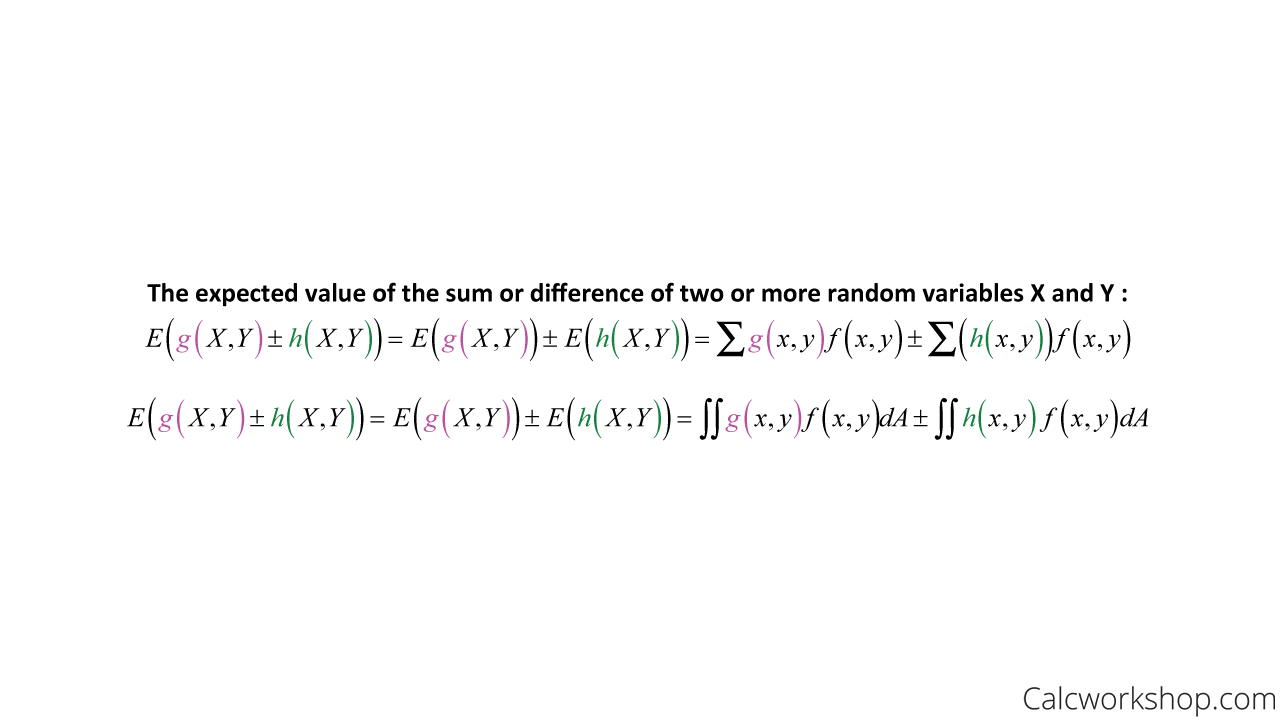
Expected Value of Two Random Variables
For example, if we let X represent the number that occurs when a blue die is tossed and Y, the number that happens when an orange die is tossed. This means we can determine their respective probability distributions and expected values and use it to calculate the expected value of the linear combination 3X – Y of the random variables X and Y:
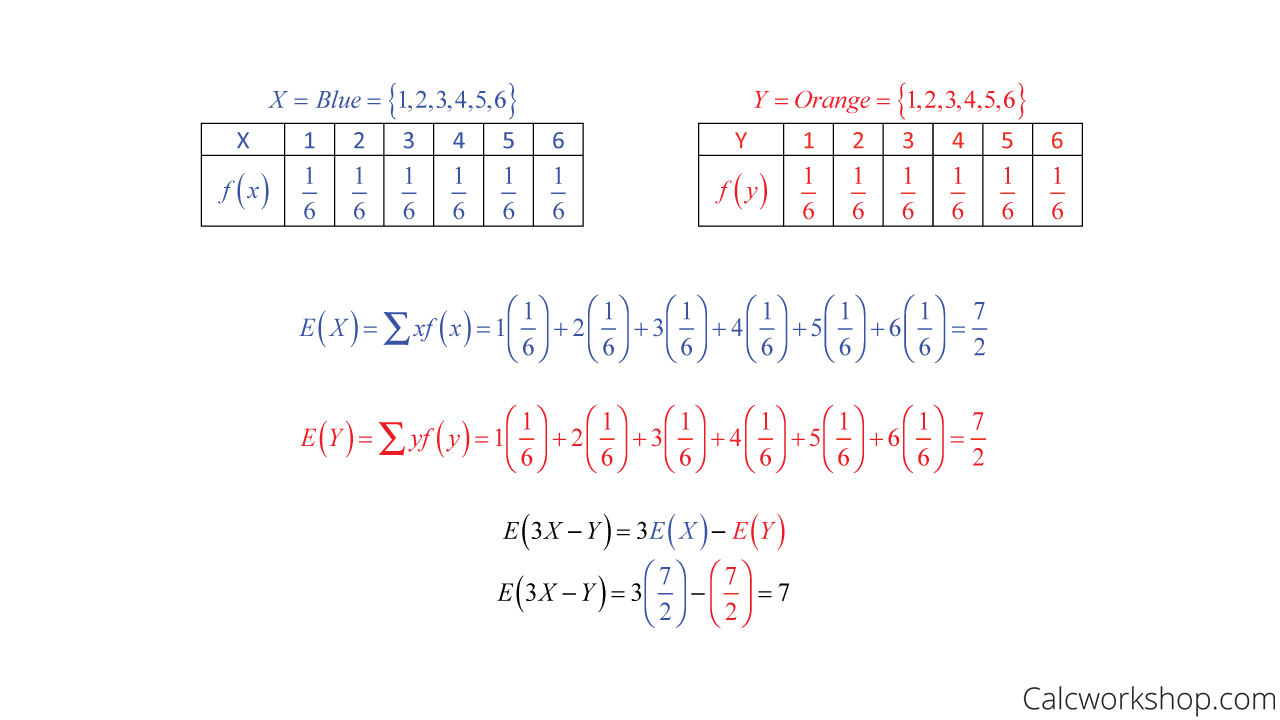
Mean And Sum Of Two Discrete Variables
And if X and Y are two independent random variables with joint density, then the expectancy, covariance, and correlation are as follows:
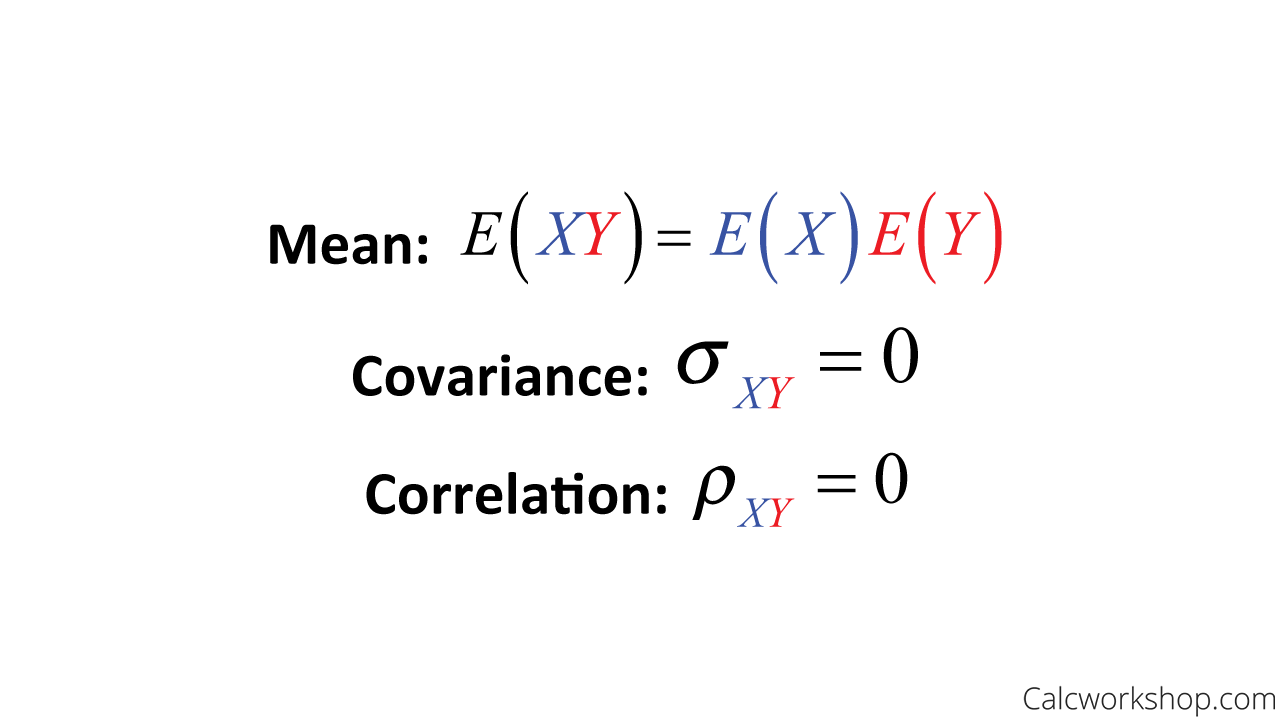
Mean, Covariance, and Correlation For Joint Variables
This following example verifies this theorem:
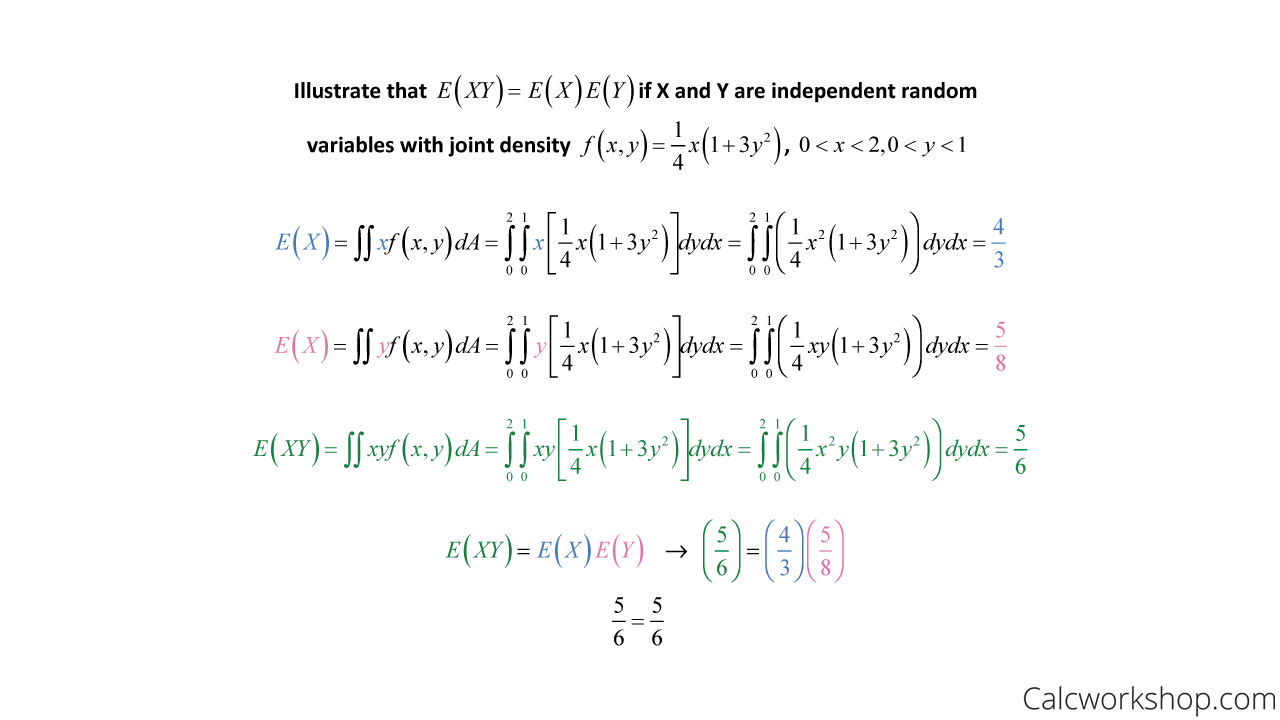
Joint Density Independence Example
And if you’ve forgotten how to integrate double integrals, don’t worry! Throughout the video, I will walk you through the process step-by-step.
And lastly, if X and Y are random variables with joint probability, then
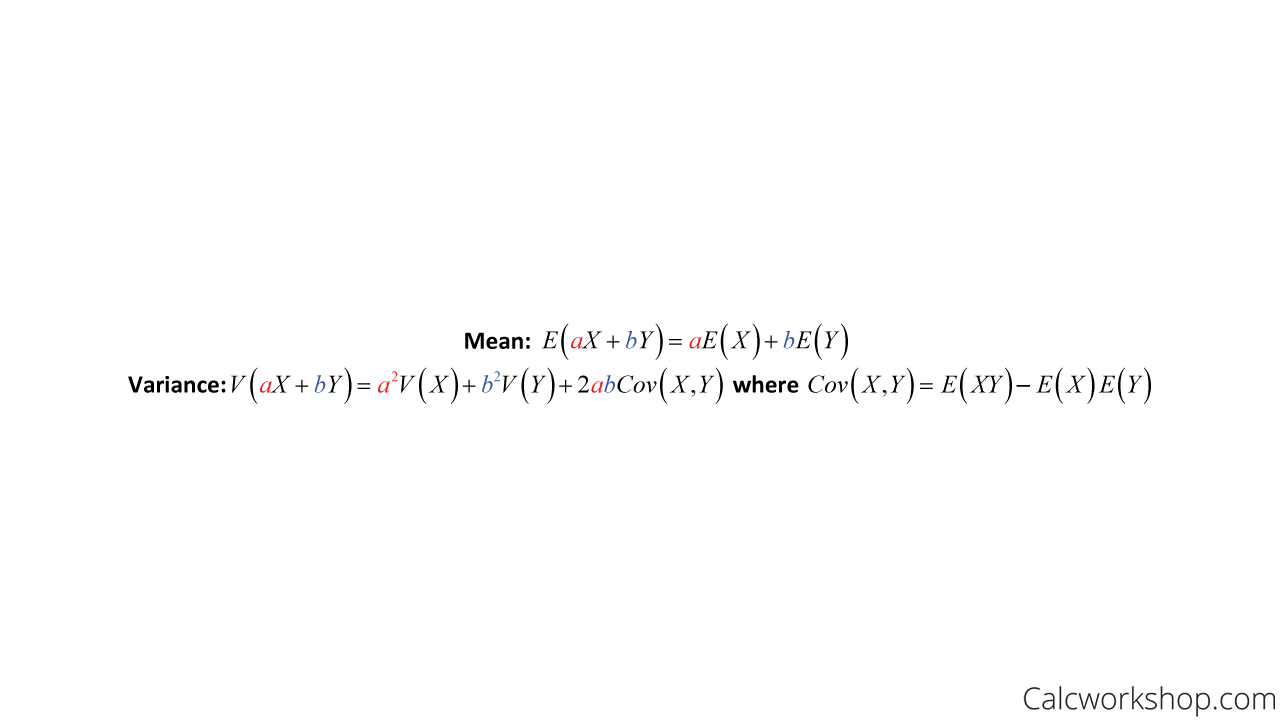
Mean And Variance Of Sum Of Two Random Variables
So imagine a service facility that operates two service lines. On a randomly selected day, let X be the proportion of time that the first line is in use, whereas Y is the proportion of time that the second line is in use, and the joint probability density function is detailed below. Find the variance of X + Y.
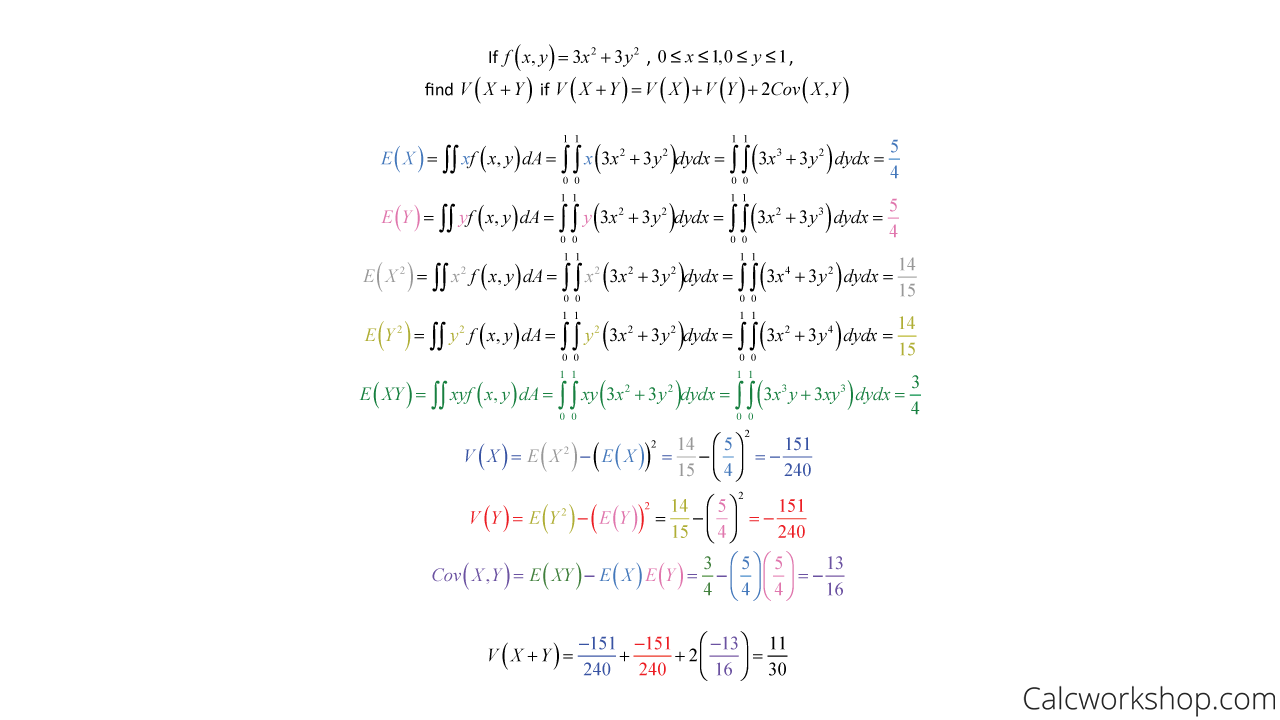
Mean And Variance For Two Continuous Variables
Together, we will work through many examples for combining discrete and continuous random variables to find expectancy and variance using the properties and theorems listed above.
Linear Combinations of Random Variables – Lesson & Examples (Video)
1 hr 40 min
- Introduction to Video: Linear Combinations of Random Variables
- 00:00:51 – Properties of Linear Combination of Random Variables
- Exclusive Content for Members Only
- 00:10:48 – Find the expected value and probability of the linear combination (Examples #1-2)
- 00:30:55 – Determine the expected value of the linear combination for continuous and discrete random variables (Examples #3-4)
- 00:31:00 – Find the expected value, variance and probability for the given linear combination (Examples 5-6)
- 01:04:25 – Find the expected value for the given density functions (Examples #7-8)
- 01:21:03 – Determine if the random variables are independent (Example #9-a)
- 01:23:58 – Find the expected value of the linear combination (Example #9-b)
- 01:31:23 – Find the variance and covariance of the linear combination (Example #9-c)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.