Did you know that the properties for joint continuous random variables are very similar to discrete random variables, with the only difference is between using sigma and integrals?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Let’s jump in!
As we learned in our previous lesson, there are times when it is desirable to record the outcomes of random variables simultaneously.
So, if X and Y are two random variables, then the probability of their simultaneous occurrence can be represented as a Joint Probability Distribution or Bivariate Probability Distribution.
Discrete Vs Continuous
So what’s the difference between joint-discrete random variables and joint-continuous random variables?
Well, it has everything to do with what is the difference between discrete and continuous. By definition, a discrete random variable contains a set of data where values are distinct and separate (i.e., countable). In contrast, a continuous random variable can take on any value within a finite or infinite interval.
Thankfully the same properties we saw with discrete random variables can be applied to continuous random variables. Still, the main difference is that we will be using integration rather than a summation.

Probability Density Function Properties
And as we previously noted, the term probability mass function, or pmf, describes discrete probability distributions, and the term probability density function, or pdf, describes continuous probability distributions.
But what really separates joint discrete random variables from joint continuous random variables is that we are not dealing with individual counts but intervals or regions. This is similar to how we found the area between two curves in both single-variable calculus and multivariable calculus.
And if you forgot how to integrate multiple integrals, don’t worry! In the video, I will remind you of the process each step of the way.
Example
So, now let’s look at an example where X and Y are jointly continuous with the following pdf:

Joint PDF
First, let’s find the value of the constant c. We do this by remembering our second property, where the total area under the joint density function equals 1.
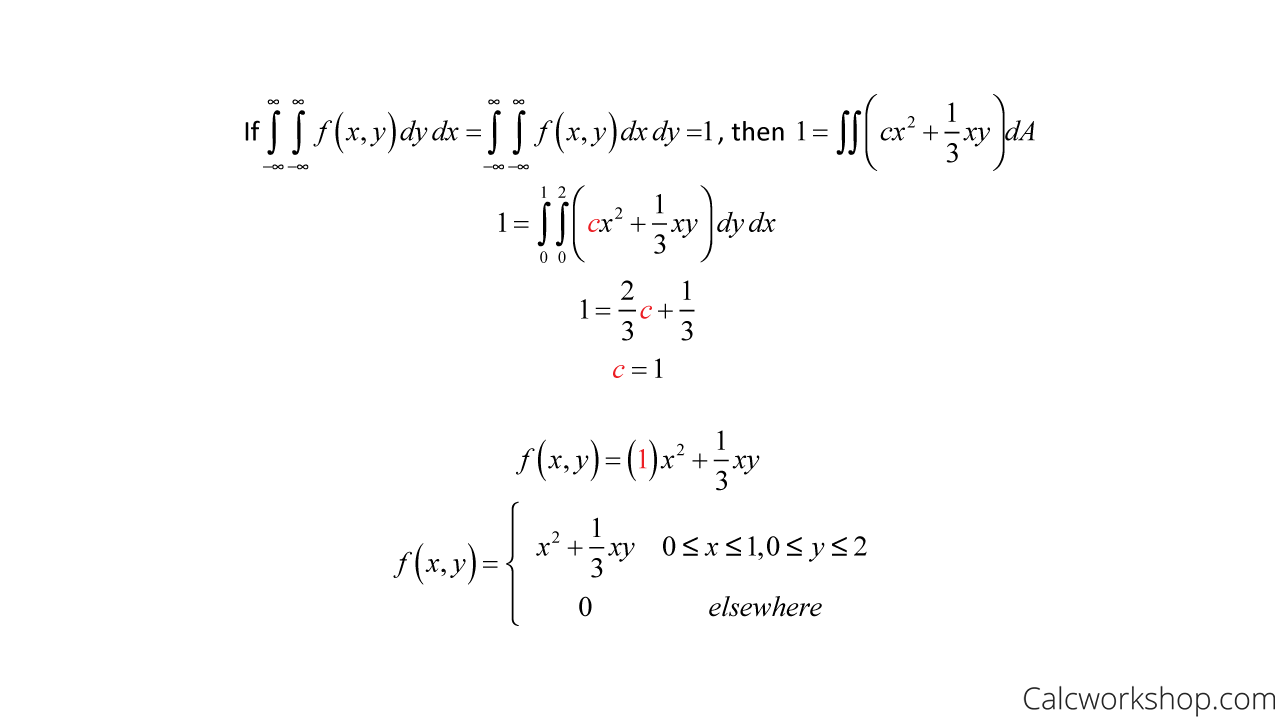
Probability Density Function Example
Next, let’s look at what would happen when we want to restrict our region to find the probability that both X and Y are greater than or equal to 1. We start drawing a picture of our region to help us identify our limits of integration and then integrate.
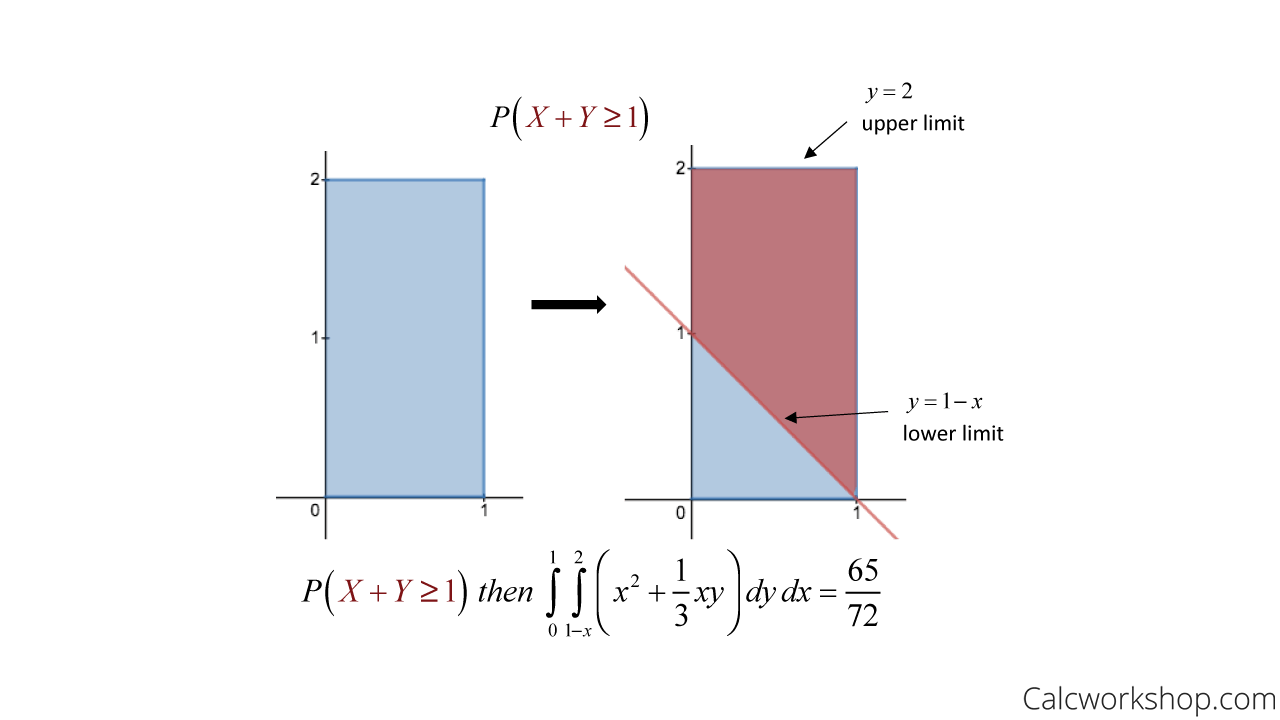
Integrate Probability Density Function Over The Range
Now another important concept that we want to look at is the idea of marginal distributions for joint continuous random variables.
The marginal distributions of X alone and Y alone are:
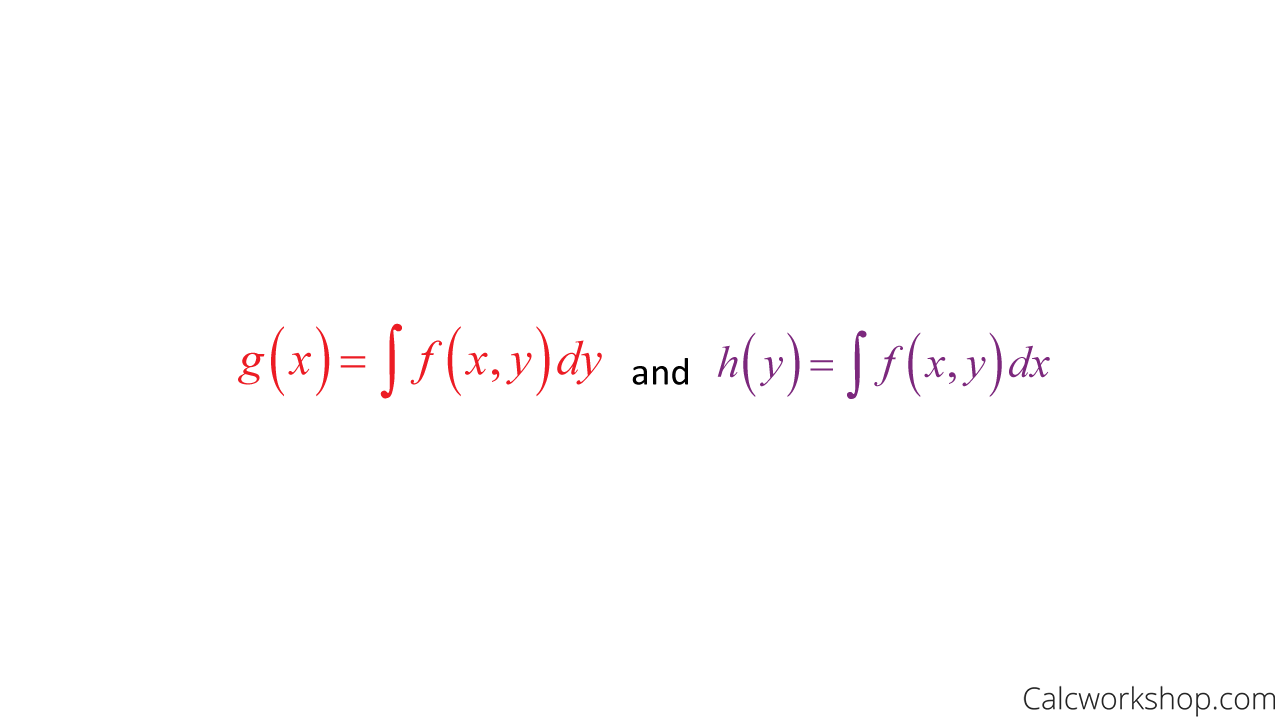
Marginal Distribution Formula For Continuous
So if we use our current example, we can find the marginal pdf for X and the marginal pdf for Y as follows:
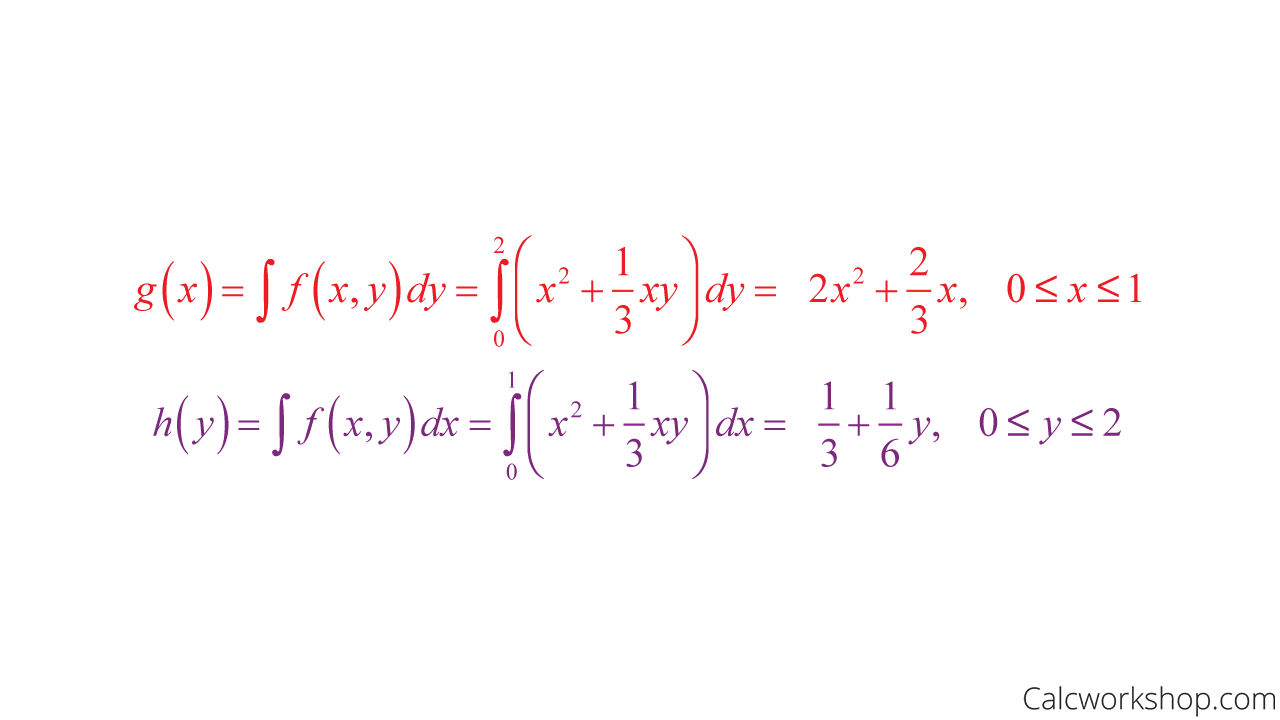
How To Find Marginal Distribution From Joint Distribution
And this leads us then to investigate the notion of conditional distributions and probability.
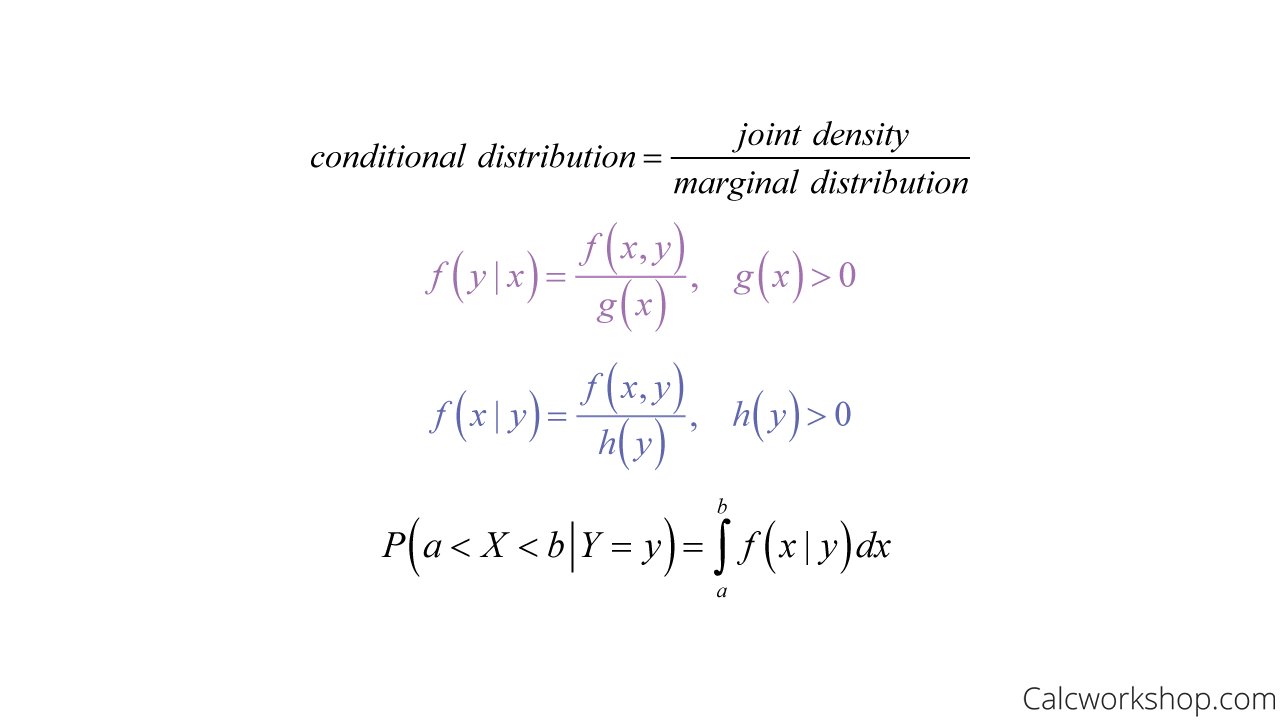
Conditional Probability Of Joint Density Function
Likewise, we can investigate independence. If X and Y are two random variables, discrete or continuous, then these variables X and Y are said to be statistically independent if and only if
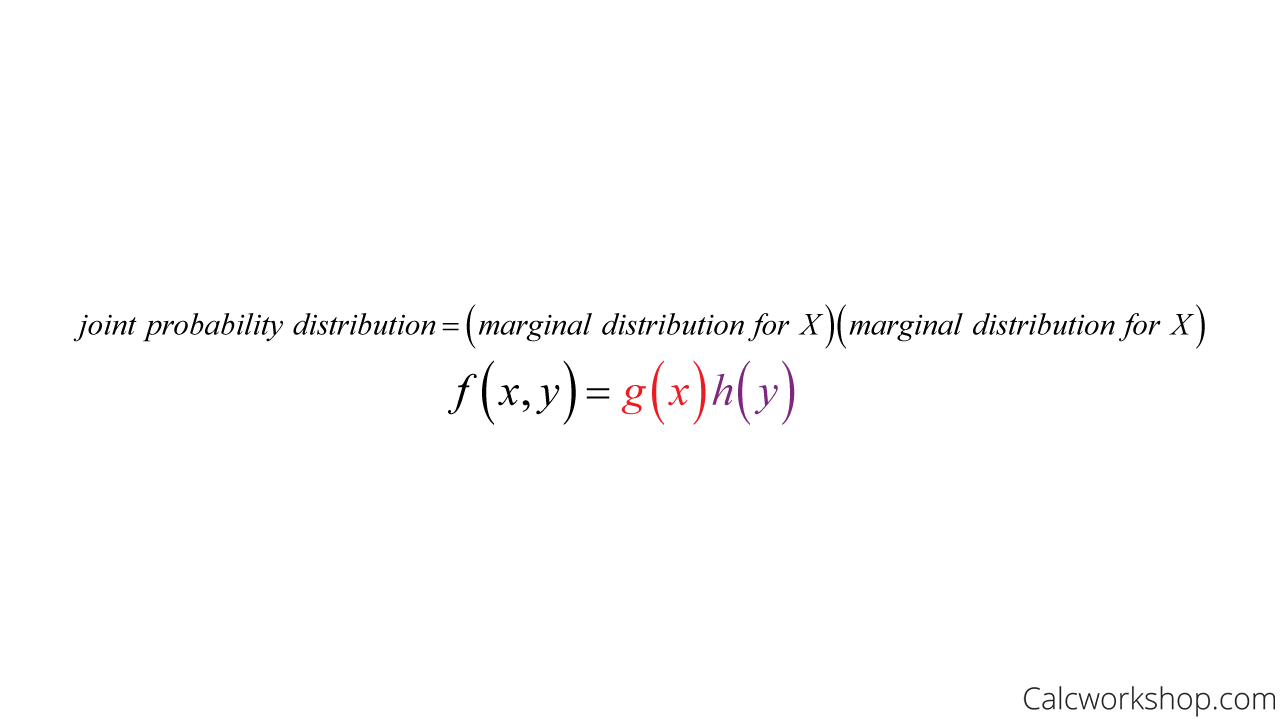
Joint Distribution Independence
And now, let’s investigate independence for our example. The easiest way to check whether X and Y are independent is to pick a point from within our shaded region and see if it satisfies our independence requirement.
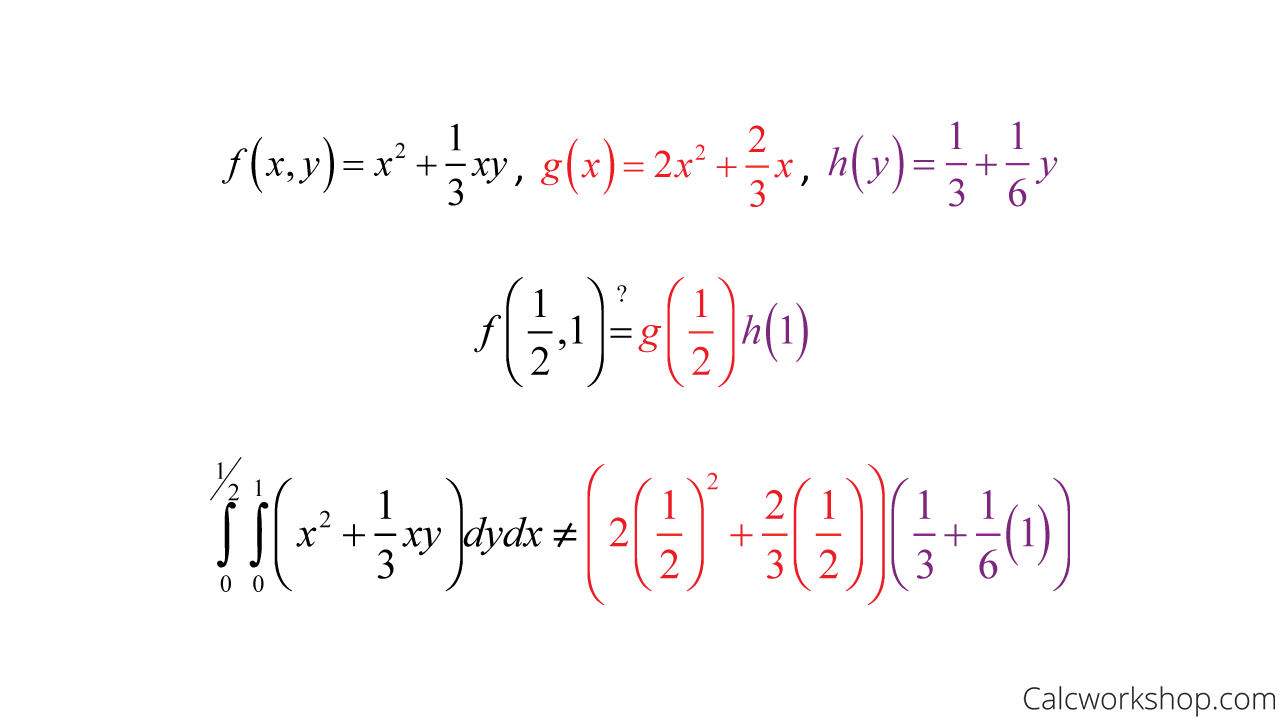
How To Determine Independence From Joint Probabilities
As you can see, for our example, X and Y are not independent.
Throughout our video lesson, we will look at countless examples, similar to this one, as we learn how to create a joint probability density function, marginal probabilities, conditional probabilities, as well mean and variance of joint continuous variables.
Joint Continuous Random Variables – Lesson & Examples (Video)
2 hr 32 min
- Introduction to Video: Joint Probability for Continuous Random Variables
- 00:00:29 – Overview of Joint and Bivariate Probability Distribution and Formulas with Example #1
- Exclusive Content for Members Only
- 00:19:30 – Consider the joint density function on the triangle with given vertices (Example #2)
- 00:43:27 – How to find Marginal distribution and Conditional distributions with Example #3
- 00:57:37 – Find the probability of the joint distribution using a triple integral (Example #4)
- 01:05:04 – Overview of Mean and Variance and Independence for Continuous Joint Probability Distributions
- 01:09:45 – Identify the marginals and conditional mean for the joint distribution (Example #5)
- 01:34:03 – Discover the marginal cdf, marginal pdf, and conditional probability (Example #6)
- 01:52:39 – Find the expected values for X and Y, marginals for X and Y, and conditional probability (Example #7)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.