Population Proportion How-To (Defined w/ 7 Examples!)

What is a population proportion?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching population proportion

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Great question!

It’s a key topic in statistical sampling, and it’s what you’re going to learn today.

Let’s go!

One Sample Proportion Test

Significance testing for population proportions means we will test a claim about a population by looking at a sample and using a sample statistic.

What this means in a practical sense is that we first start by writing our hypothesis statement, using p as the population proportion.

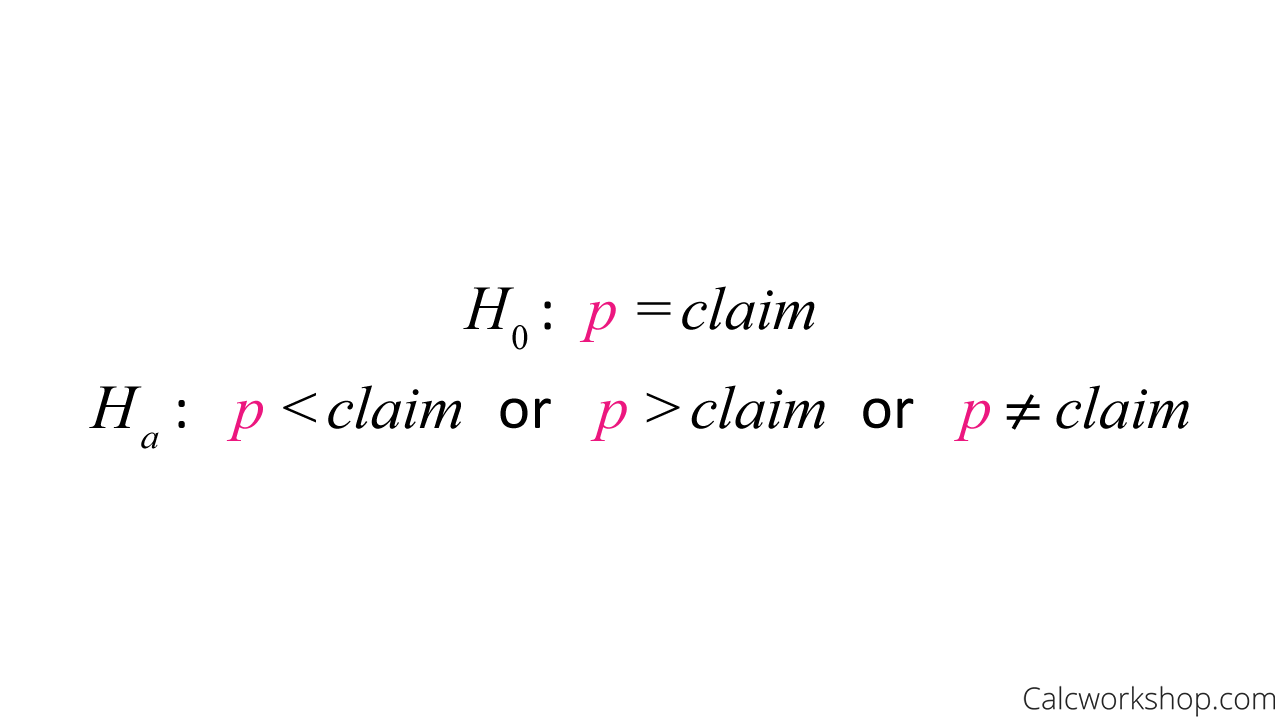
Null and Alternative Hypothesis of Proportions

Next, we test this claim by using our sample and finding our test statistic.

One Proportion Z Test Statistic

Then we calculate the p-value, which is the probability of getting our sample statistic, or something more extreme if our null hypothesis is true.

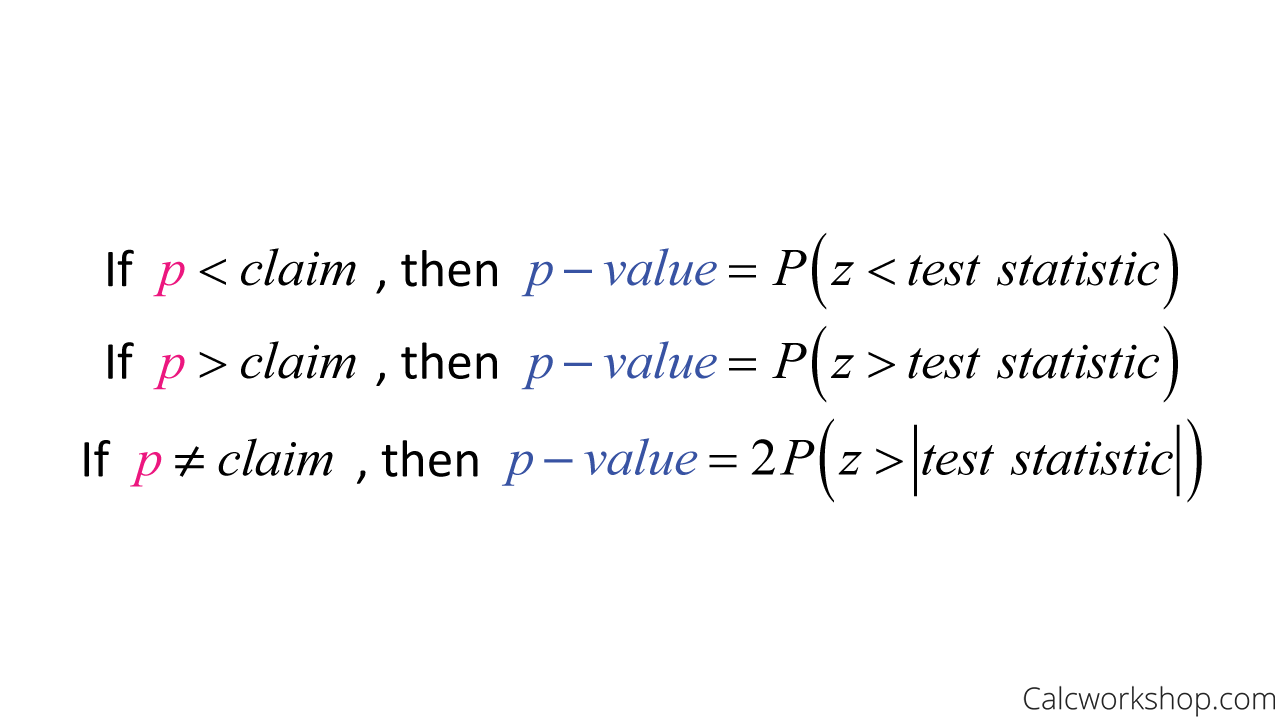
How To Calculate P Value

And lastly, we draw our conclusions by comparing our p-value to the significance level as discussed by Stat Trek, and similarly as how we determined our confidence level.

If our p-value is small, we reject our null hypothesis and have significant evidence to conclude the alternative.

In contrast, if it is large, we fail to reject our null hypothesis.

What Does P Value Mean

Two Sample Proportion Test

But there are often times when we want to compare two groups. For example:

Maybe we’re interested to know if a SAT prep course really helps to improve scores.
Or what proportion of people will vote for a certain candidate.
Or does a new drug treatment really work?

These situations deal with the comparison of two populations: those who took an SAT prep course and those who did not. Those who vote for a particular candidate and those who do not. Those that improved with a new drug treatment and those who did not.

Now there are two reasons why estimated proportions are different:

It’s complete happenstance (chance).
Or there truly is a difference in the populations.

How do we determine the truth?

By conducting a hypothesis test for the difference of population proportions.

Now, just like a one-sample proportion test, the difference between two proportions follows an approximately normal distribution. This means we’ll be using a z-table to find our probability values. Additionally, you will find that testing for significance for a difference in two population proportions follows very similar steps as for a one-sample test.

First, we list our parameters and statistics.

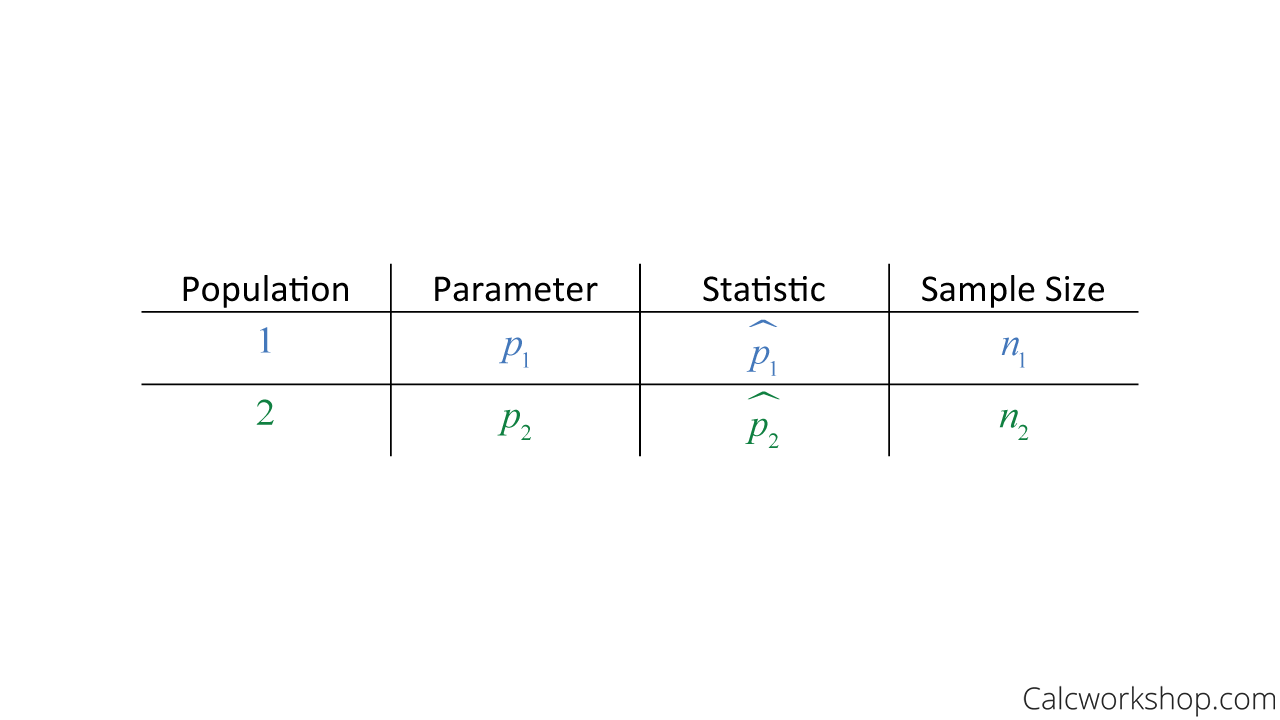
Parameter — Statistic

Next, we state our null hypothesis and alternative hypothesis

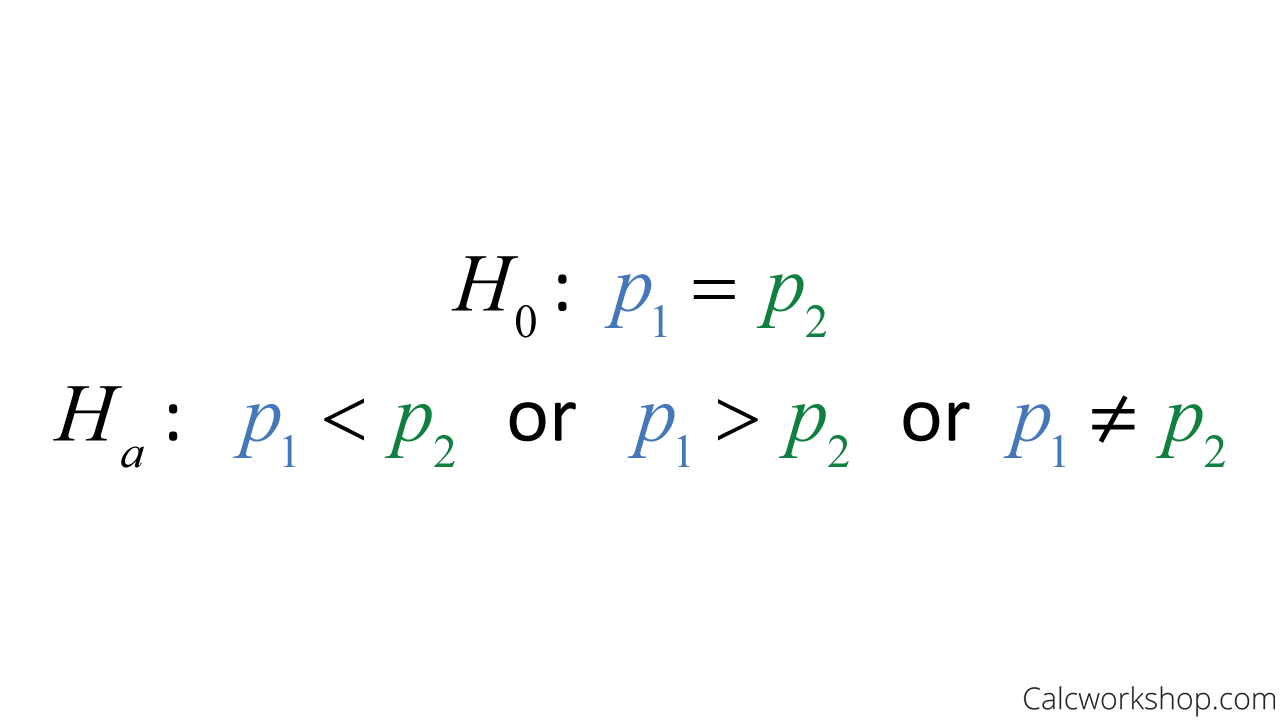
Null Alternative Two Proportions Test

And now, we’re ready to calculate our test statistic. But please note that we will be pooling our variances.

Pooled Variance

Pooling variances, or pooled variances, means we will combine both variances to find an overall variance. In essence, we are going to assume that the variance of each population is the same.

So, now we use the following formula to calculate our test statistic and find our p-value.

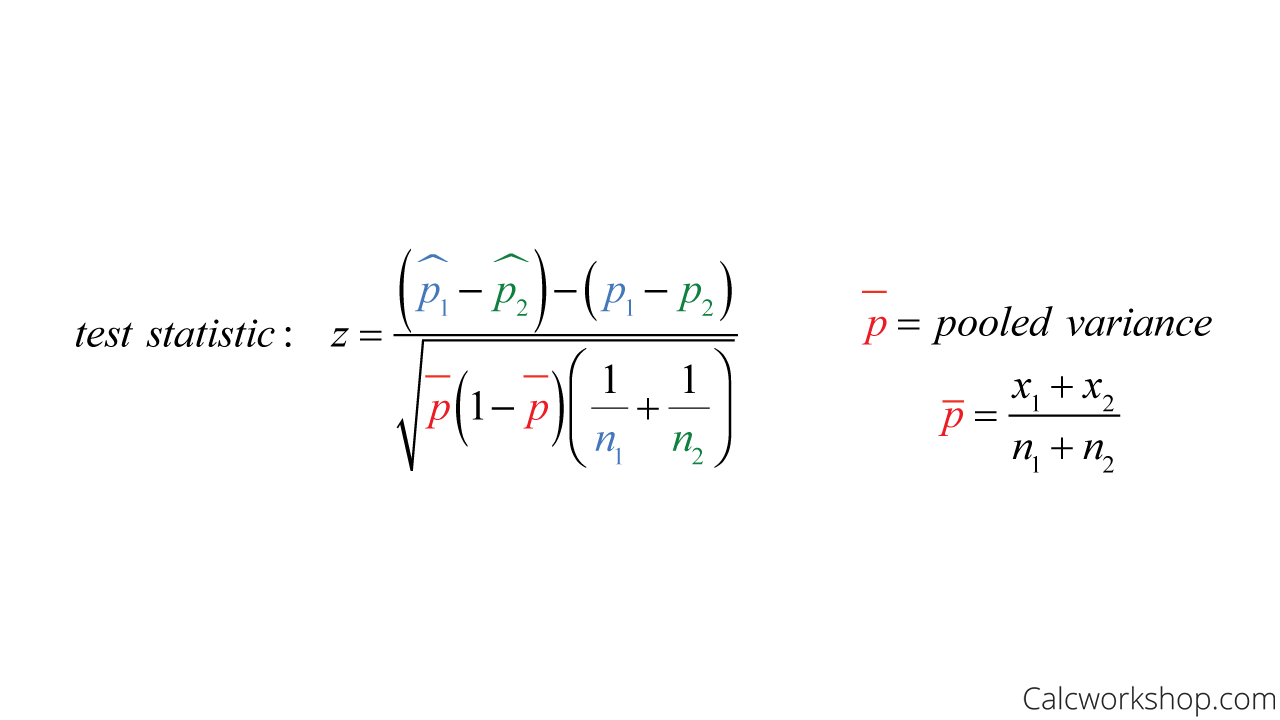
Test Statistic For 2 Proportion Z Test

Then we compare this number to our significance level, like we did for one-sample proportions, and draw the necessary conclusion.

Worked Example

For example, suppose we want to compare the proportion of children who receive a free or reduced lunch at two different schools.

If a random sample size 80 students from School 1 reveals 19 students receive a free or reduced lunch and a random sample size 100 students from School 2 shows 26 students receive a free or reduced lunch, does the data give evidence of a difference in the population proportions. (Assume a normal distribution and a significance level of 0.05.)

Two Sample Population Proportion Test — Example

Thus showing that there is no significant evidence to conclude that the proportions of students at the two schools who receive free or reduced lunch are different.

Overall, hypothesis testing for population proportions is really straightforward, and we are going to work through countless examples to ensure understanding and mastery.

Population Proportion – Lesson & Examples (Video)

1 hr 10 min

Introduction to Video: Hypothesis Test for Population Proportions
00:00:33 – Overview of hypothesis tests for proportions and understanding the p-value and significance level
Exclusive Content for Members Only

00:10:06 – Test for significance using a one-tail z-test (Examples #1-2)
00:23:21 – Construct a hypothesis test for a two-tail z-test (Example #3)
00:30:14 – Create a hypothesis test and provide a confidence interval (Example #4)
00:40:48 – How to create a hypothesis test for the difference of two population proportions (Example #5)
00:52:57 – Construct a hypothesis test and provide a confidence interval for the difference of proportions (Example #6)
01:03:01 – Create a hypothesis test for the difference of population proportions (Example #7)
Practice Problems with Step-by-Step Solutions
Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.