Did you know that a surjective function focuses on the codomain?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
And that’s exactly what you’re going to learn about in today’s discrete lesson.
Let’s go!
What Is A Surjective Function
While we know that a function is a relation (set of ordered pairs) in which no two ordered pairs have the same first element, we want to focus our attention to a special type of function called a surjection.
In other words, nothing in the codomain is left out.
This means that for all “bs” in the codomain there exists some “a” in the domain such that a maps to that b (i.e., f(a) = b).
Simply put, when the range equals the codomain, then the function is onto!

Surjection Definition
Mapping Diagram
For example, let’s look at the following two mapping diagrams to see if we can spot a surjective function.
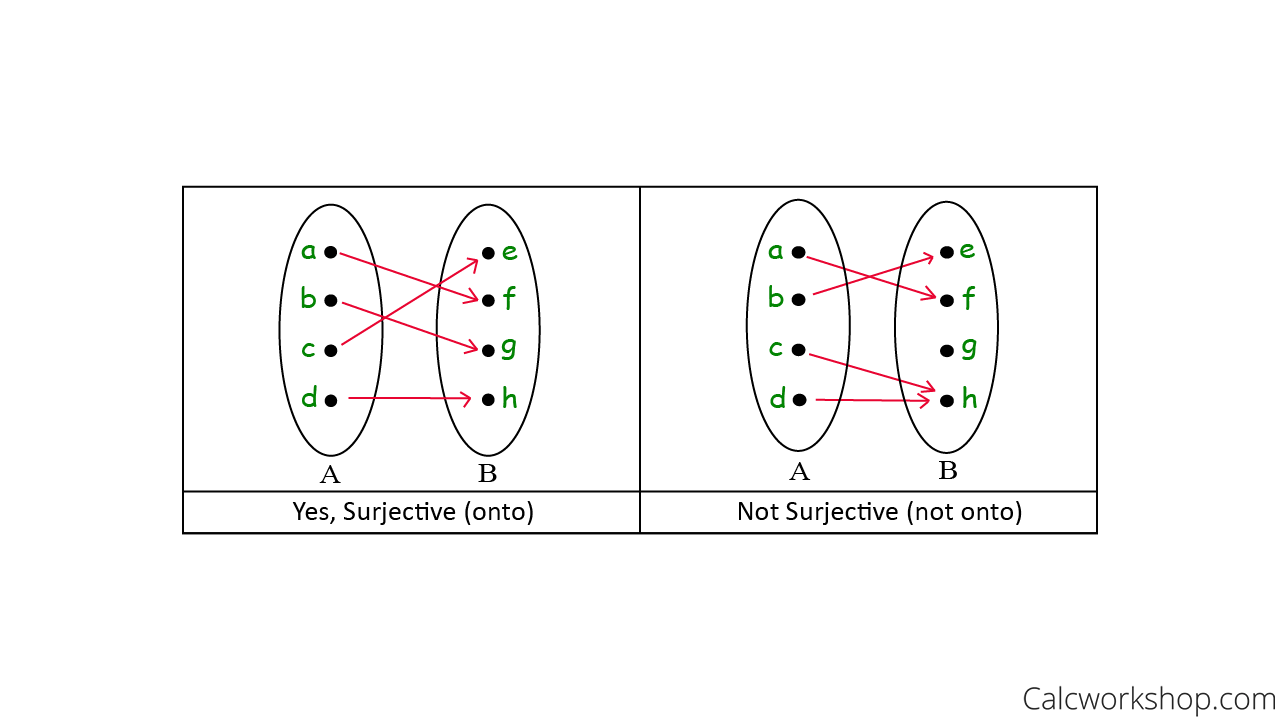
Onto Vs Not Onto
Notice that the arrow diagram on the left is a surjection because every element in the codomain (B) is mapped to from some element in the domain A. But the arrow diagram on the right is not a surjection because not every element in the codomain (B) is mapped to — poor little g doesn’t have a buddy.
Relation
So, how do we go about proving whether a function is surjective or not?
Well, depending on how the function is given (i.e., relation, arrow diagram, graph, or equation) will dictate the strategy that you use. Let’s work through a few examples so you can get the idea.
When you are given either a mapping diagram or a relation, all you have to do is compare the elements in the codomain with the elements in the range. If all the values match, then the function is onto, otherwise the function is not onto, as the example below demonstrate.
Example
The relation on the left is onto because every element in the codomain is “hit” at least once by an element in the domain, whereas the relation on the right is not onto because element of 2 in the codomain is not used.

Surjection Sets — Example
Graph
Whenever we are given a graph, the easiest way to determine whether a function is a surjections is to compare the range with the codomain. If the range equals the codomain, then the function is surjective, otherwise it is not, as the example below emphasizes.
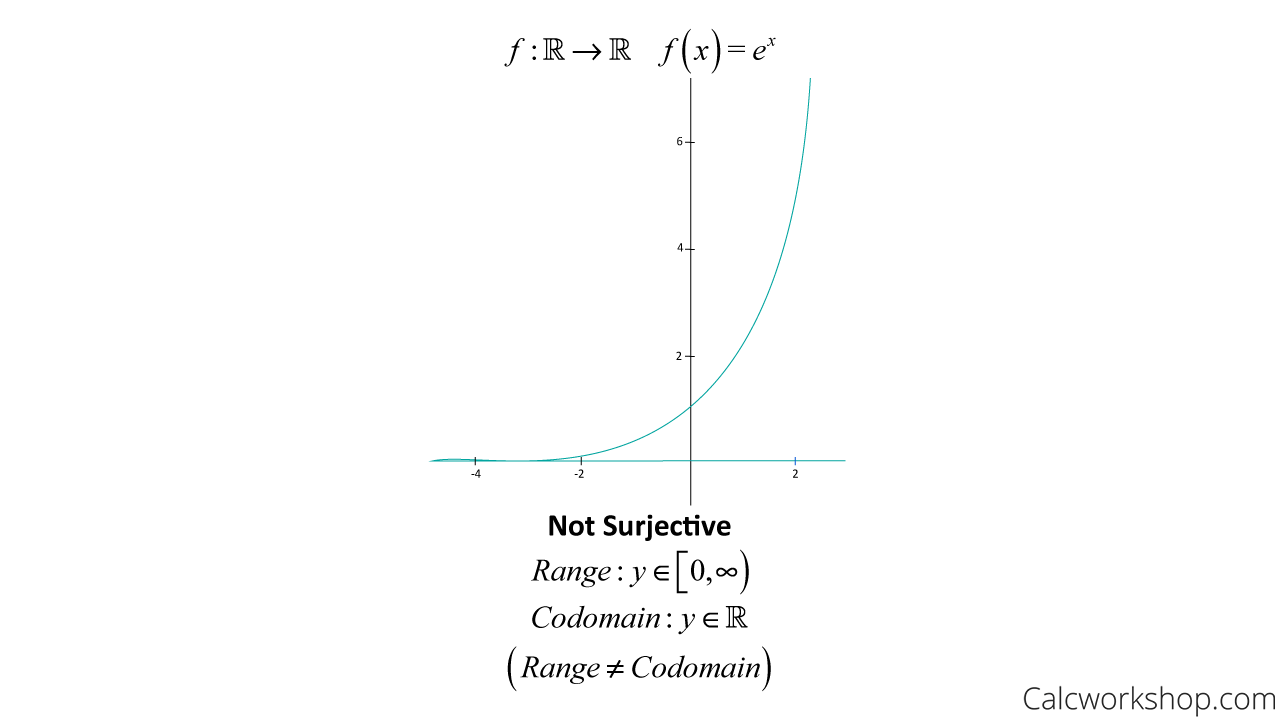
Surjection Graph — Example
Proof
How do you prove a function is a surjective function?
The key to proving a surjection is to figure out what you’re after and then work backwards from there. For example, suppose we claim that the function f from the integers with the rule f(x) = x – 8 is onto.
Now we need to show that for every integer y, there an integer x such that f(x) = y. What this means is that if we take our equation y = x-8 and solve for x we can than work backwards toward our goal.

How To Prove Onto
See, not so bad!
Together we will learn how to prove whether a function is surjective using various techniques such as mapping diagrams, graphs, relations, and direct proofs. Additionally, we will discover how to create surjective functions over open regions and determining.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
51 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.