Did you know that some functions never assign the same value to two different domain elements?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
These types of functions are said to be injective, or one-to-one.
What Is An Injective Function
As we learned in our previous lesson, types of functions, a function has two key requirements, noted by Virginia Commonwealth University.
- Every element in the domain has an image under f.
- Every element in the domain has a unique image.
In other words, every element in A (domain) has exactly one “buddy” in B (codomain or image).
All this means is that for a function to be one-to-one every distinct element in A has a distinct image in B.

Injective Definition
Mapping Diagrams For Functions
For example, let’s look at the following arrow diagrams. The mapping on the left shows an injunction because every element in A maps to a “unique buddy” in B. However, the mapping on the right is not an injunction because two elements in A (a and d) map to the same element in B (4), therefore they don’t have a “unique buddy.”
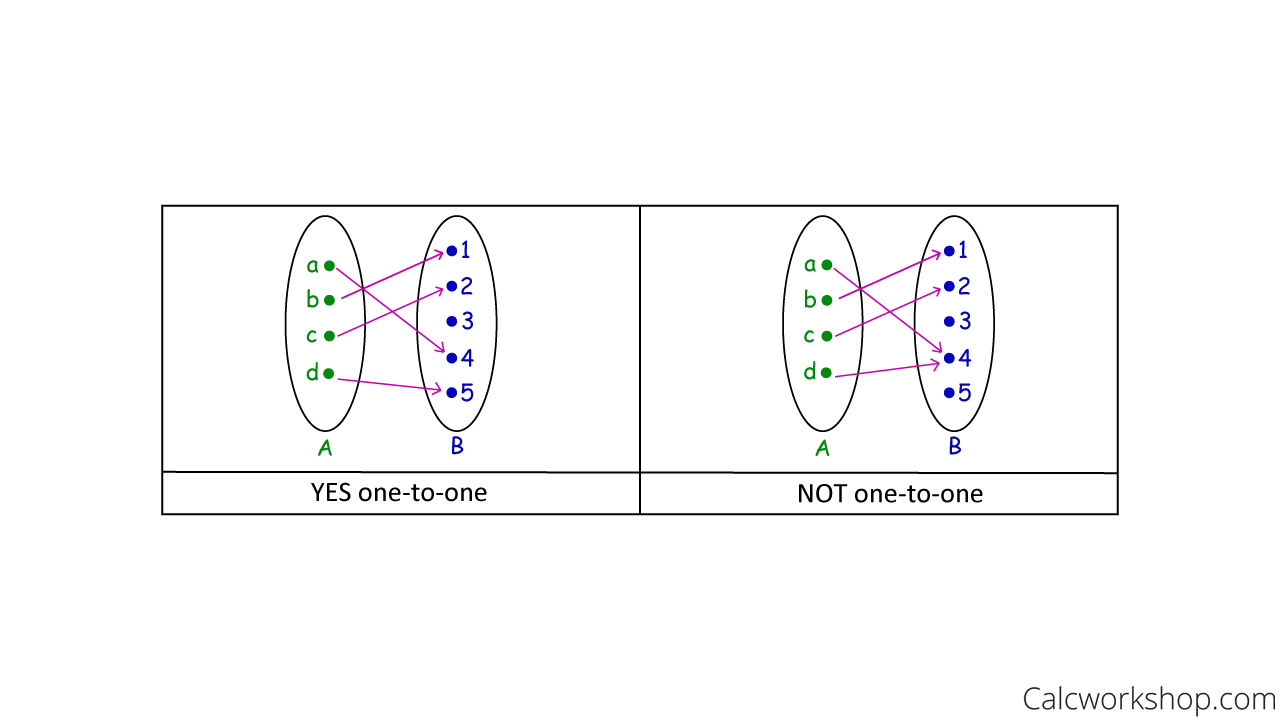
Arrow Diagram — Injective
What Does The Horizontal Line Test Prove
Additionally, we can also use the Horizontal Line Test (HLT) as it is a convenient way to determine one-to-one functions.
All we have to do is draw a horizontal line through the graph of a function and if it intersects the graph only once, then the function is one-to-one as the example below nicely highlights.
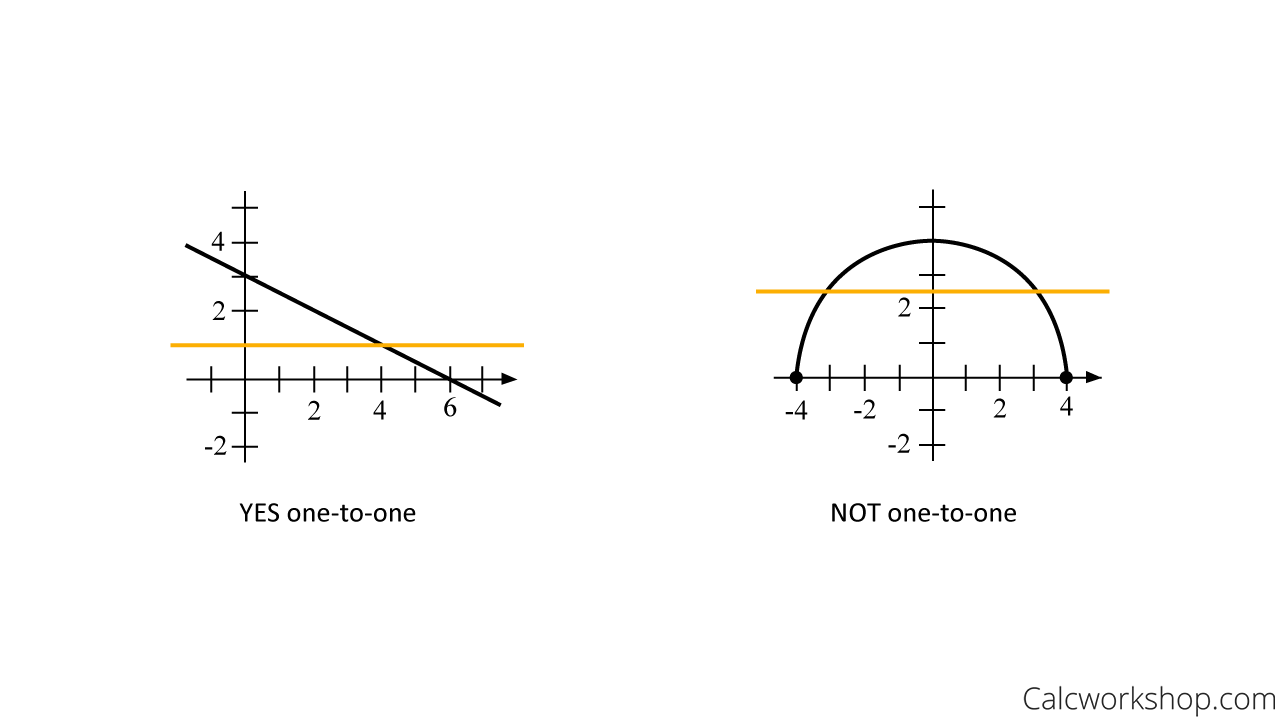
Horizontal Line Test Examples
Cool!
But the HLT does have its limitations, as it assumes you are given a function that you can graph over the real numbers.
Direct Proofs For One-To-One
So how do we prove whether or not a function is injective?
To prove a function is injective we must either:
- Assume f(x) = f(y) and then show that x = y.
- Assume x doesn’t equal y and show that f(x) doesn’t equal f(x).
The following two example will help to sort this out!
Example #1
For our first example, if x is defined on the integers let’s prove that f(x) is a one-to-one function.

Prove One To One — Example
See, not so bad!
Example #2
Okay, for our second example, we will use our steps for proving injective functions to show that f(x) is not one-to-one.
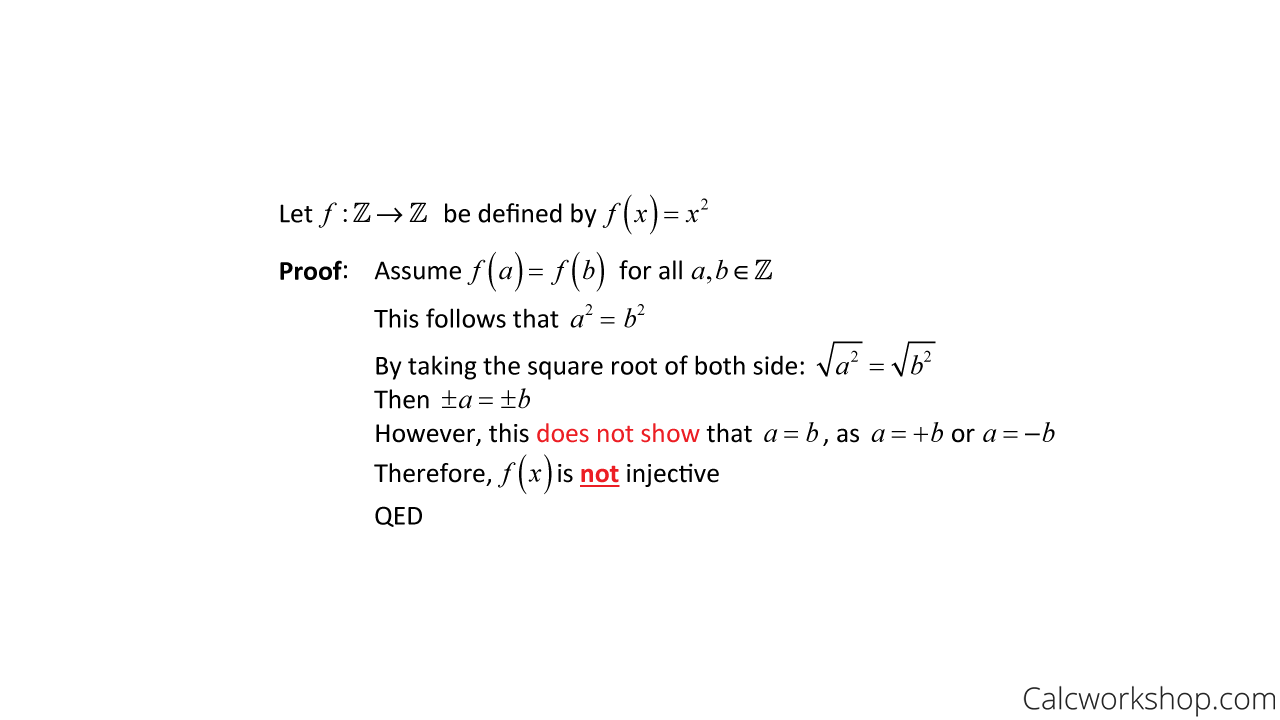
Prove Not One To One — Example
Thus, if a doesn’t equal b, then f(a) doesn’t equal f(b).
Now, did you know we can also apply some of our calculus skills to help us guarantee a function is one-to-one?
Interestingly enough, a real function is injective if it is strictly increasing or entirely decreasing within the open region.

Increasing Decreasing Function Definition
First Derivative Test For Injective Testing
So, how do we determine if a function is increasing or decreasing?
We apply our first derivative test from Calculus!
If we can show that the first derivative is positive (i.e., f’(x) > 0 ) over the open interval (a,b) then we have shown f(x) is increasing. Similarly, if we can verify that the first derivative is negative (i.e., f’(x) < 0 ) over the open interval (a,b) then we have shown f(x) is decreasing.
For example, let’s show the following function is injective by using calculus.
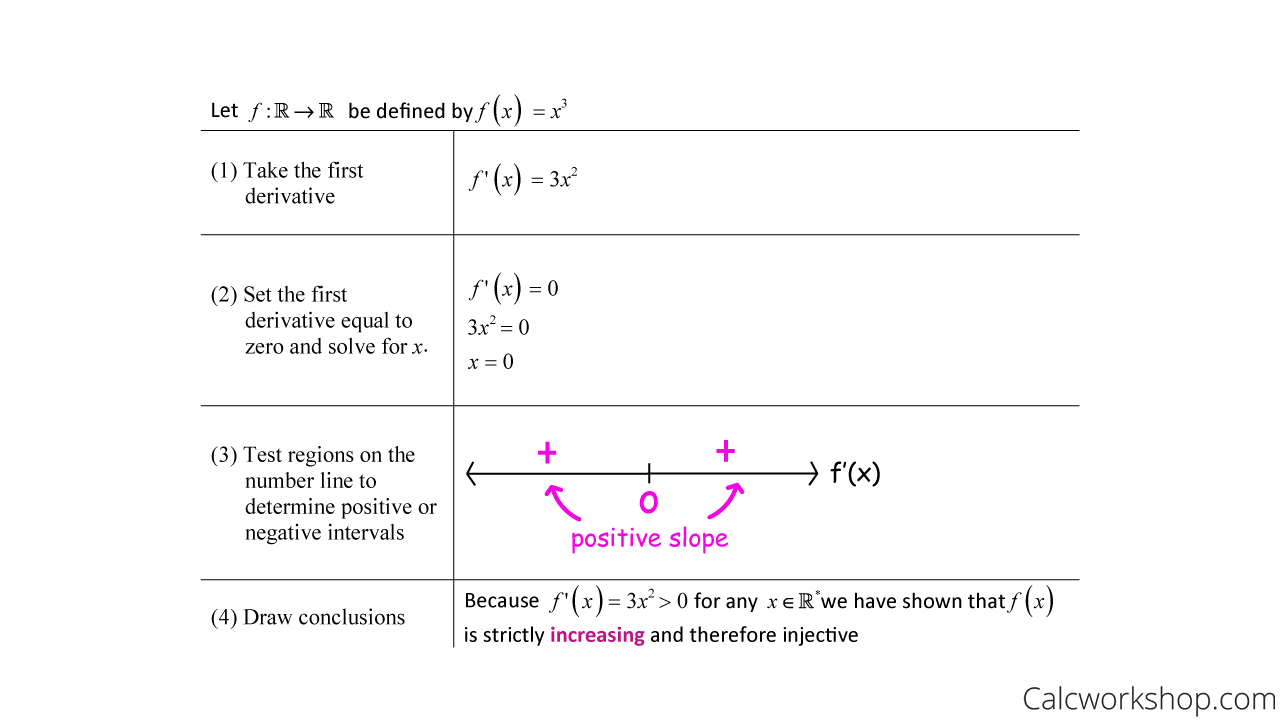
Strictly Increasing Verify Injective
Together we will learn how to prove whether a function is injective using various techniques such as mapping diagrams, horizontal line test, direct proofs, and calculus. Additionally, we will discover how to create injective functions over open regions and determining whether a function is well-defined.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 14 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.