Did you know that a bijection is another way to say that a function is both one-to-one and onto?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Is A Bijection
A bijection, also known as a one-to-one correspondence, is when each output has exactly one preimage.
In other words, each element in one set is paired with exactly one element of the other set and vice versa.
But how do we keep all of this straight in our head? How can we easily make sense of injective, surjective and bijective functions?
Here’s how.
Focus on the codomain and ask yourself how often each element gets mapped to, or as I like to say, how often each element gets “hit” or tagged.
- Injective: Elements in the codomain get “hit” at most once
- Surjective: Elements in the codomain get “hit” at least once
- Bijective: Elements in the codomain get “hit” exactly once
Worked Example
So, now it’s time to put everything we’ve learned over the last few lessons into action, and look at an example where we will identify the domain, codomain, and range, as well as determine if the relation is a function, if it is well-defined, and whether or not it is injective, surjective or bijective.

Injective — Surjective — Bijective
Setup
- Let A={a, b, c, d}, B={1, 2, 3, 4}, and f maps from A to B with rule f = {(a,4),(b,2),(c,1),(d,3)}.
- Domain: {a,b,c,d}
- Codomain: {1,2,3,4}
- Range: {1,2,3,4}
Questions
- Is f a function? Yes, because all first elements are different, and every element in the domain maps to an element in the codomain.
- Is f well-defined? Yes, because the domain of f equals set A.
- Is f injective? Yes, every element in the codomain is “hit” at most once.
- Is f surjective? Yes, ever element in the codomain is “hit” at least once, and the range of f equals B.
- Is f bijective? Yes, because f is both injective and surjective.
See how easy that was? All we had to do was ask “at most, at least, or exactly once” and we got our answer!
Nice!
Invertible Function
And did you know that there’s something really special about a bijective function?
A bijective function is also an invertible function.
Knowing that a bijective function is both one-to-one and onto, this means that each output value has exactly one pre-image, which allows us to find an inverse function as noted by Whitman College.
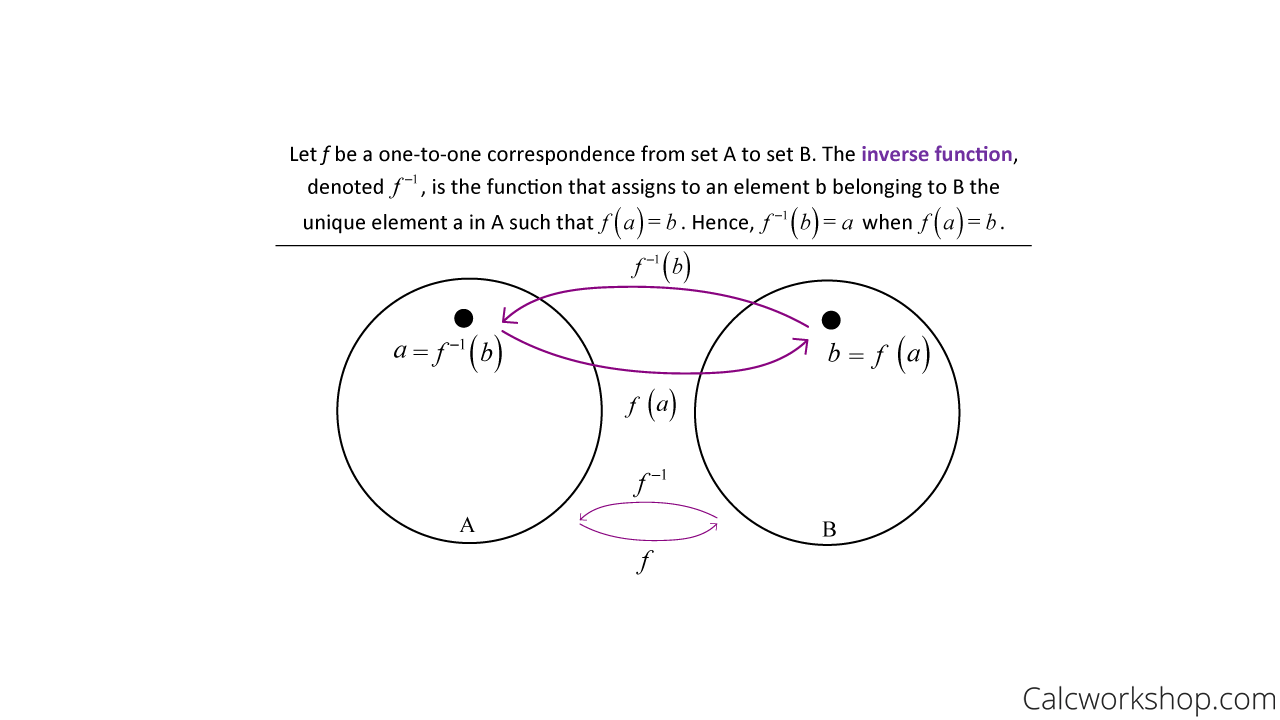
Bijection Inverse — Definition
Theorems
Additionally, there are some important properties and theorems related to bijective function and inverses

Theorems Inverse Functions
Now if you recall from your study in precalculus, the find the inverse of a function, all we do is switch our x and y variables and then resolve the equation for y.
Well, guess what?
That’s exactly what we’re going to do here too!
Proof – In Detail
Alright, so let’s look at a classic textbook question where we are asked to prove one-to-one correspondence and the inverse function.
Suppose f is a mapping from the integers to the integers with rule f(x) = x+1. Show that f is bijective and find its inverse.

How To Prove A Function Is Bijective
Summing Up…
- You will learn how to prove one-to-one correspondence by determining injective and surjective properties in discrete math.
- You will discover important theorems relevant to bijective functions.
- You will understand how a bijection is also invertible.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 11 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.