Have you ever pondered your chances of survival amid an earthquake, tornado, or being lost in an unfamiliar wilderness?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
While a select few might feel equipped for such challenges, many of us would be left feeling overwhelmed. That’s why preparation for potential disasters is essential.
Interestingly, planning for the worst isn’t exclusive to adventure-seekers and risk-management gurus. It’s also a fundamental principle for computer scientists as they examine algorithms’ time and space complexity.
Welcome to asymptotic notation, where exploring the growth of functions paves the way for crafting algorithms that outperform rivals and optimize efficiency.
Envision a function, any function. In the beginning, with small data, things might seem chaotic. But as the data increases, approaching infinity, we start to see the function’s true nature – its end behavior, or asymptotic efficiency.
The Asymptotic Notation Dream Team: Big-O, Big-Omega, and Big-Theta
Meet the notable trio, the algorithmic task force, the asymptotic notation team:
Big-O (Big-Oh), the Worrier: Always ready for the worst-case scenarios, Big-O sets the upper bound for a function’s growth. He’s the one ensuring that chaos remains under control.
Big-Omega, the Optimist: Full of positivity, Big-Omega focuses on the lower bound and the best-case scenario. This notation encourages the algorithm to reach for optimal performance.
Big-Theta, the Realist: The one who bridges the gap between the Worrier and the Optimist, Big-Theta represents the asymptotically tight bound. This notation harmonizes the upper and lower bounds of Big-O and Big-Omega, ensuring balance and unity.
Together, these three algorithmic partners guide us through the captivating world of function growth, equipping us with the knowledge to create efficient algorithms.
Let’s take a closer look at each one.
Big-O (Big-Oh) Notation
Definition: Let \(f\) and \(g\) be functions from the set of integers or real numbers to the set of real numbers. We say that f(x) is O(g(x)), if there are positive constants \(C\) and k such that:
\begin{equation}
|f(x)| \leq C|g(x)| \text { when } x>k
\end{equation}
Wow, that’s a mouthful!
Okay, so what this really means is that f(x) is big-O of g(x), denoted f(x) is O(g(x)), if \(g\) asymptotically dominates \(f\).
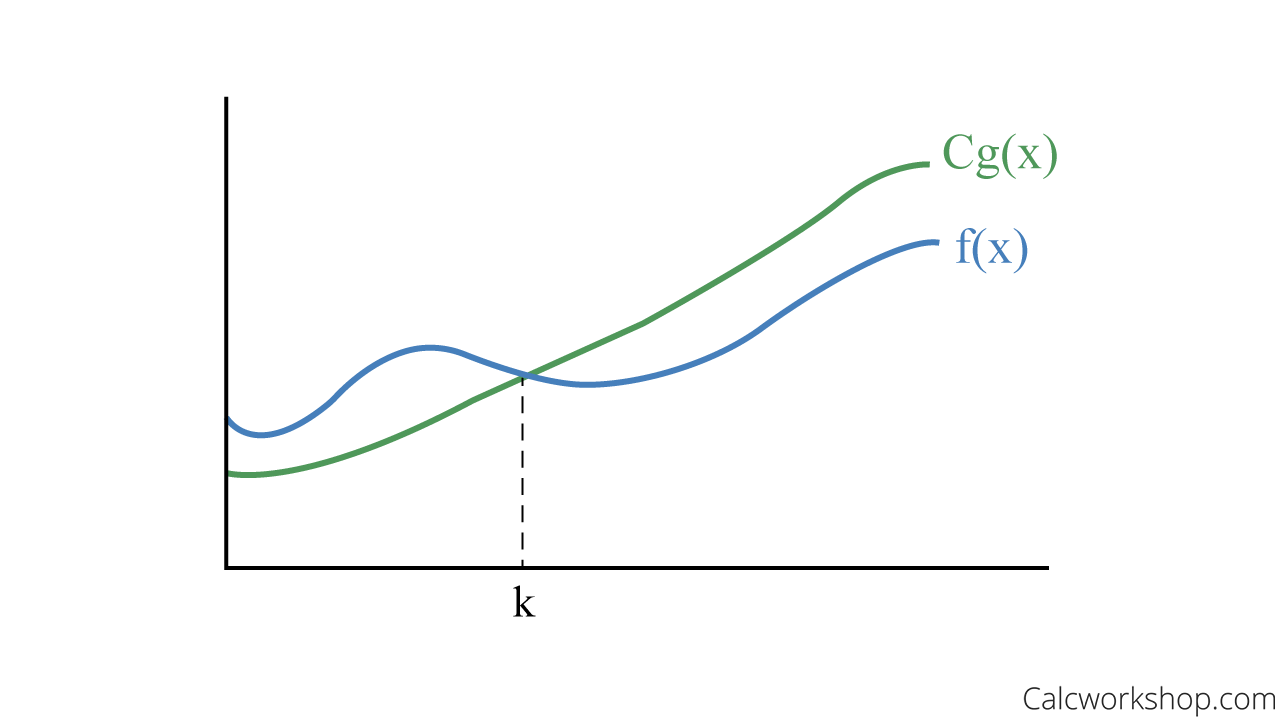
Big Oh – Upper Bound Graph
In other words, if we can understand the asymptotic limiting behavior of functions, we can see the long-term effect for large input values.
Thus, we can use Big O as the upper bound for the growth of a function and help us predict the worst-case scenario.
This analysis is aided using the following properties for big-O and its complexity classes.
Properties of Big-O
- If \(f_1(x)=O\left(g_1(x)\right)\) and \(f_2(x)=O\left(g_2(x)\right)\), then \(\left(f_1+f_2\right)(x)=O\left(\max \left|g_1(x)\right|,\left|g_2(x)\right|\right)\)
- If \(f_1(x)=O\left(g_1(x)\right)\) and \(f_2(x)=O\left(g_2(x)\right)\), then \(\left(f_1 f_2\right)(x)=O\left(g_1(x) g_2(x)\right)\)
- If \(f_1(x)\) and \(f_2(x)\) are both \(O(g(x))\) then \(\left(f_1+f_2\right)(x)=O(g(x))\)
- If \(f(x)\) is \(O(g(x))\), then \((a f)\) is \(O(g)\) for any constants
Complexity classes for Big-O:
\begin{equation}
\begin{array}{ll}
O(1) \text { constant } & O(\log n) \log a r i t h m i c \\
O(n) \text { linear } & O(n \log n) \text { linearithmic (quasilinear) } \\
O\left(n^2\right) \text { quadratic } & O\left(n^c\right) \text { polynomial } \\
O\left(2^n\right) \text { exponential } & O(n !) \text { factorial }
\end{array}
\end{equation}
This is easily observed in the following graph, where our function is arranged, so they are big-O of the next function.
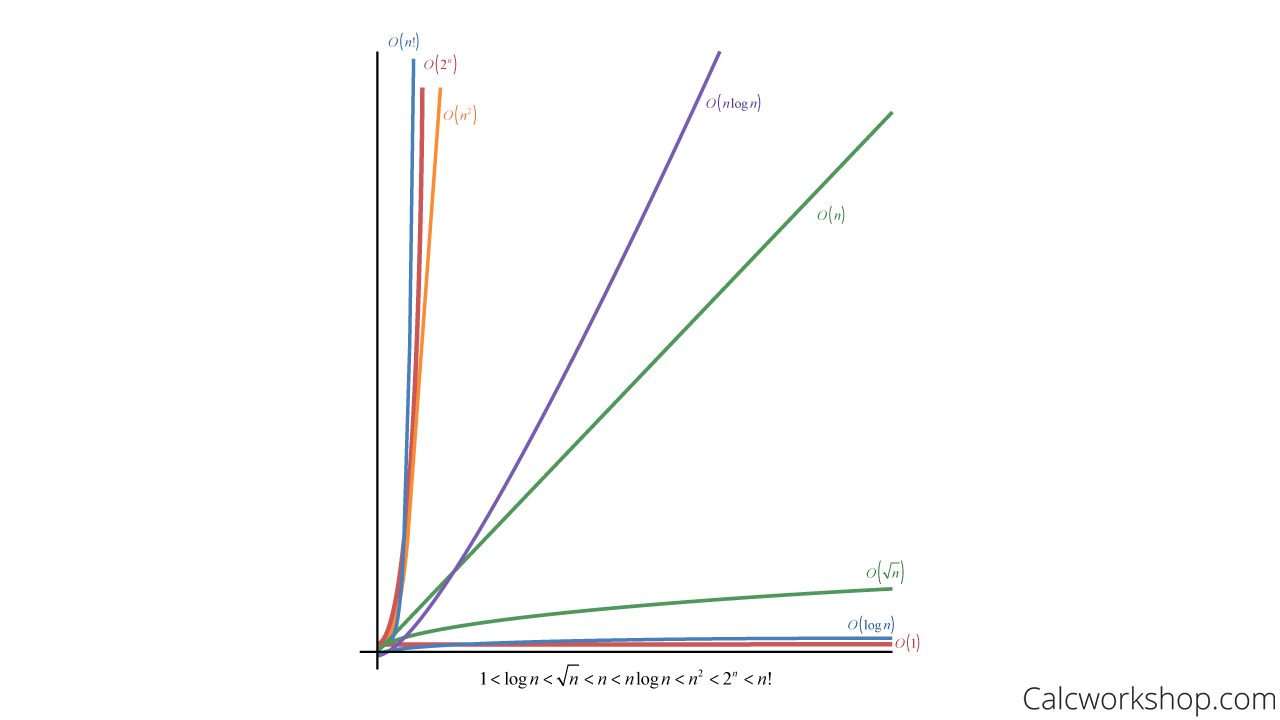
Functions Arranged In Big Oh Order
As we can see, the constant \(y = 1\) will eventually become the smallest function, whereas \(y = n!\) will ultimately become the largest function in terms of growth.
Big-\(\Omega \) (Omega) Notation
Definition: Let \(f\) and \(g\) be functions from the set of integers or real numbers to the set of real numbers. We say f(x) is big-Omega of g(x), denoted f(x) is \(\Omega \left( {g\left( x \right)} \right)\), if there are witness \(C\) and \(k\), which are positive constants, such that:
\begin{equation}
|f(x)| \geq C|g(x)| \text { when } x>k
\end{equation}
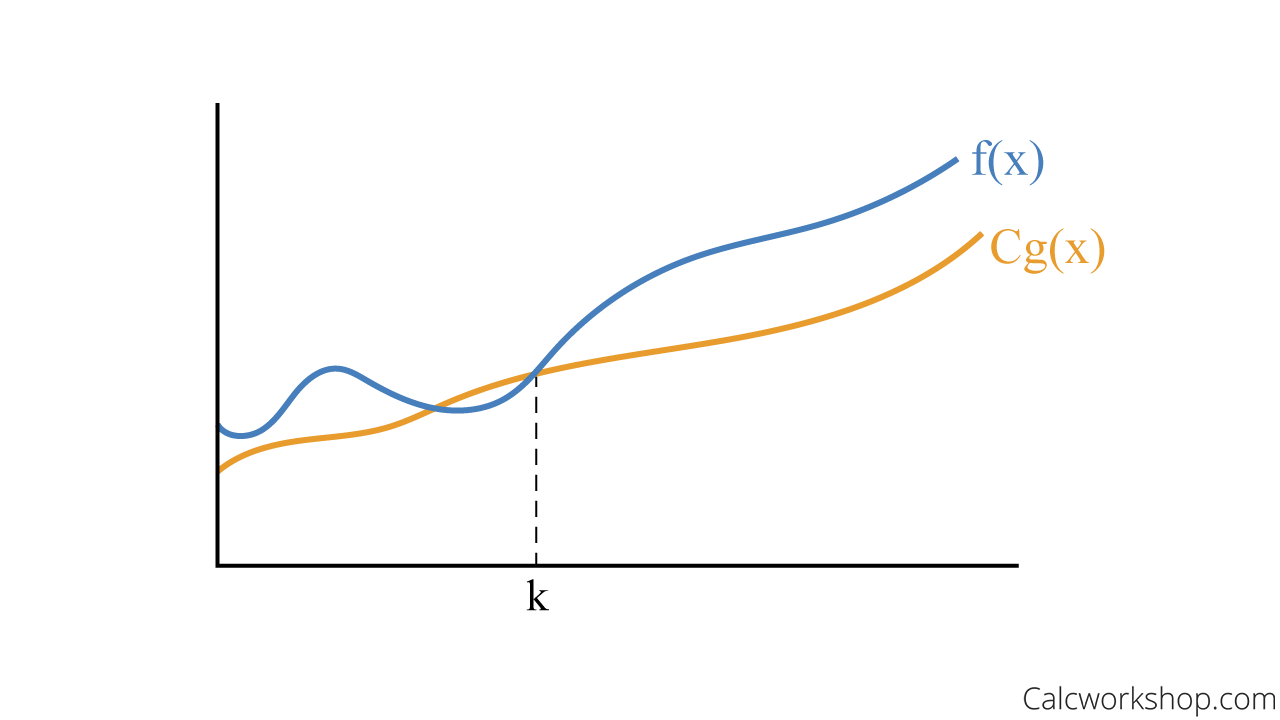
Big Omega – Lower Bound Graph
In a nutshell, Big-Omega is the lower bound, indicating the best-case scenario. It tells us that an algorithm’s runtime is at least this much.
Big-\(\Theta \) (Theta) Notation
Definition: Let \(f\) and \(g\) be functions from the set of integers or real numbers to the set of real numbers. We say f(x) is big-theta of g(x), denoted f(x) is \(\Theta \left( {g\left( x \right)} \right)\), if f(x) is O(g(x)) and f(x) is \(\Omega \left( {g\left( x \right)} \right)\). Therefore, f(x) is \(\Theta \left( {g\left( x \right)} \right)\) if and only if there are positive constants \({c_1}\), \({c_2}\), and k, such that
\begin{equation}
c_1|g(x)| \leq f(x) \leq c_2|g(x)| \text { when } x>k
\end{equation}
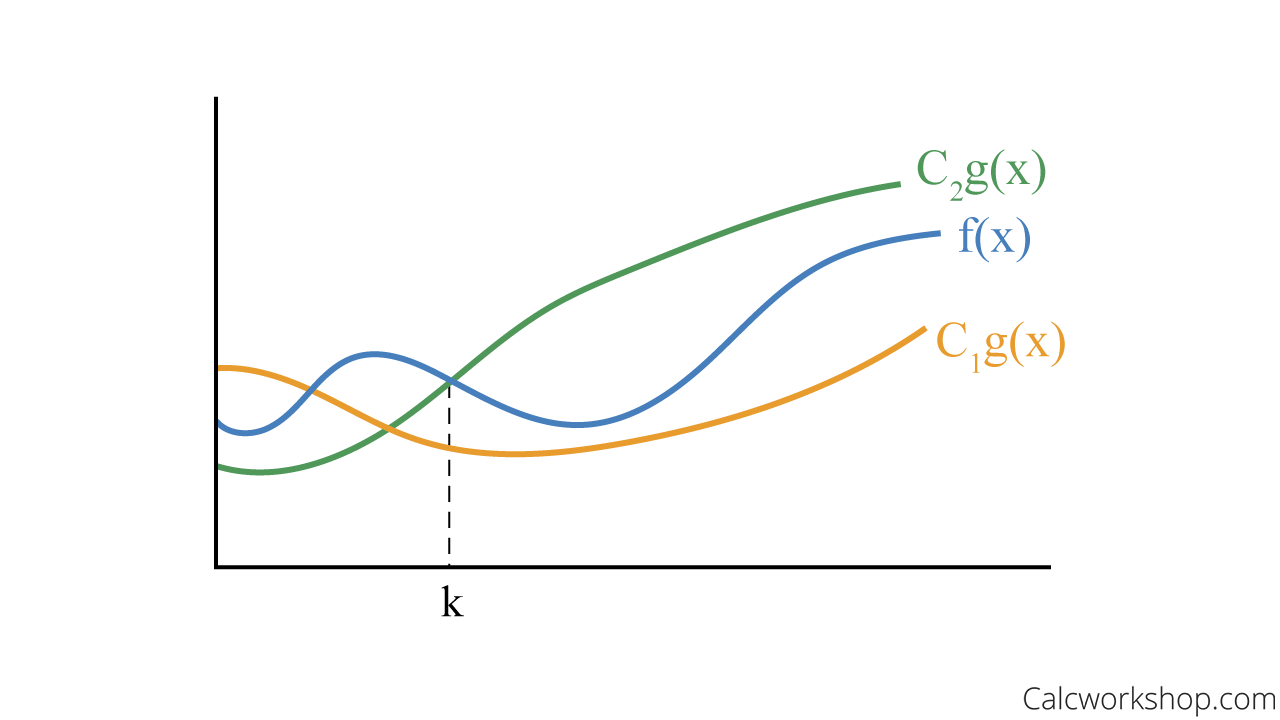
Big Theta – Tight Bound Graph
To put it simply, Big-Theta is considered an asymptotically tight bound.
Key Insights
Now, the formal definitions of big O, big Omega, and big theta require us to find specific witnesses, which are the constants \(C\) and \(k\), but in practice, we don’t really care what those constants are, just that they exist.
This is similar to convergence in calculus. While it is undoubtedly important to know what a series or sequence precisely converges to, just knowing that it does converge is what really matters.
Alright, let’s find out how to determine asymptotic complexity and leave the specifics of finding witnesses for our next lesson.
Asymptotic Limit Theorems
The three asymptotic notations (\(O,\Omega,\Theta \)) are related to the definition of a limit from calculus. As we focus on large inputs of \(n\) (i.e., as \(n\) approaches infinity), the runtime will follow an asymptotic relationship between \(f\) and \(g\), provided the limit exists.
\begin{equation}
\text { If } \lim _{n \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=0 \text {, then } f(x) \text { is } O(g(x))(\mathrm{Big}-\mathrm{O})
\end{equation}
\begin{equation}
\text { If } \lim _{n \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=\infty \text {, then } f(x) \text { is } \Omega(g(x)) \text { (Big-Omega) }
\end{equation}
\begin{equation}
\text { If } \lim _{n \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=L \text {, where } 0<L<\infty \text {, then } f(x) \text { is } \Theta(g(x)) \text { (Big-Theta) }
\end{equation}
So, all we have to do is apply a limit at infinity, and we can quickly determine the growth of a function!
Cool! Let’s look at a few examples.
Three Examples
Using the asymptotic limit theorems, determine \(O\left( {} \right)\), \(\Omega \left( {} \right)\), or \(\Theta \left( {} \right)\).
1. If \(f\left( x \right) = 9 + 4{x^2}\) and \(g\left( x \right) = {x^2}\), does
\begin{equation}
f(x) = O(g(x)), \Omega(g(x)), \text { or } \Theta(g(x))?
\end{equation}You’ll notice that as \(x\) goes to infinity, the numerator and denominator also go to infinity because they have the same degree. Therefore, we divided the leading coefficients and obtained a value of 4.
\begin{equation}
\lim _{x \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=\lim _{x \rightarrow \infty}\left(\frac{9+4 x^2}{x^2}\right)=\frac{4}{1}=4
\end{equation}Since 4 is a positive value between zero and infinity, f(x) is big-Theta of g(x). Using our limit theorems, we can say:
\begin{equation}
f(x)=\Theta\left(x^2\right)
\end{equation}Furthermore, we now know that there are constant values constants \({c_1}\), \({c_2}\), and k, such that f(x) is both \(O\left( {g\left( x \right)} \right)\) and \(\Omega \left( {g\left( x \right)} \right)\).
2. If \(f\left( x \right) = 3{x^3} – 5x\) and \(g(x)=x^2\), does
\begin{equation}
f(x) = O(g(x)), \Omega(g(x)), \text { or } \Theta(g(x))?
\end{equation}You’ll notice as \(x\) goes to infinity, and the numerator goes to infinity faster than the denominator because it has a larger degree. Therefore, the limit approaches infinity.
\begin{equation}
\lim _{x \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=\lim _{x \rightarrow \infty}\left(\frac{3 x^3-5 x}{x^2}\right)=\infty
\end{equation}This indicates that f(x) is big-Omega of g(x). Using our limit theorems, we can say:
\begin{equation}
f(x)=\Omega\left(x^2\right)
\end{equation}where there are witnesses \(C\) and \(k\) such that \(\left| {f\left( x \right)} \right| \ge C\left| {g\left( x \right)} \right|\) when \(x>k\).
3. If \(f\left( x \right) = 7\log x\) and \(g\left( x \right) = x\), does
\begin{equation}
f(x) = O(g(x)), \Omega(g(x)), \text { or } \Theta(g(x))?
\end{equation}To find out, we will need to apply L’Hopital’s Rule to evaluate the indeterminate form:
\(\lim _{x \rightarrow \infty}\left(\frac{f(x)}{g(x)}\right)=\lim _{x \rightarrow \infty}\left(\frac{7 \log x}{x}\right)=\frac{\infty}{\infty} \stackrel{\substack{\text { Appply } \\ \text { L. Hopital’s } \\ \text { Rule }}}{=} \lim _{x \rightarrow \infty}\left(\frac{\left(\frac{7}{x}\right)}{1}\right)=\lim _{x \rightarrow \infty}\left(\frac{7}{x}\right)=\frac{7}{\infty}=0\) And you’ll see as \(x\) goes to infinity, the denominator goes to infinity faster than the numerator because it has a larger degree. Therefore, the limit approaches zero.
\(\lim _{x \rightarrow \infty}\left(\frac{7 \log x}{x}\right)^{\substack{L \text { ‘Hopital’s } \\ \text { Rule }}}=\lim _{x \rightarrow \infty}\left(\frac{\left(\frac{7}{x}\right)}{1}\right)=\lim _{x \rightarrow \infty}\left(\frac{7}{x}\right)=\frac{7}{\infty}=0\) This indicates that f(x) is big-Oh of g(x). Using our limit theorems, we can say:
\begin{equation}
f(x)=O(x)
\end{equation}
See how easy it is to determine the growth of a function using limits?
Summary
In summary, we’ll breeze through oodles of examples to identify if a function is Big-O (upper bound), Big-Omega (lower bound), or Big-Theta (tight bound) using limit theorems. The world of asymptotic notation awaits, so let’s get crackin’!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.