Simplify Fractions
Easy How-To w/ 8 Step-by-Step Examples!

How to simplify fractions?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Great question!

And in today’s math lesson, you’re going learn two different methods to do just that.

Overview

The word simplify means to make something easier to do or understand.

So, reducing or simplifying fractions means we make the fraction as simple as possible.

We do this by dividing the numerator and the denominator by the largest number that can divide into both numbers exactly. In other words, we divide the top and bottom by the biggest number they have in common.

Note that the numerator and denominator are called “terms” of a fraction. So, if we simplify a fraction, we reduce the fraction to the simplest terms.

For example, notice the three rectangles below where the left-hand side of each rectangle is shaded and the fraction that results represents the shaded part out of the whole rectangle.

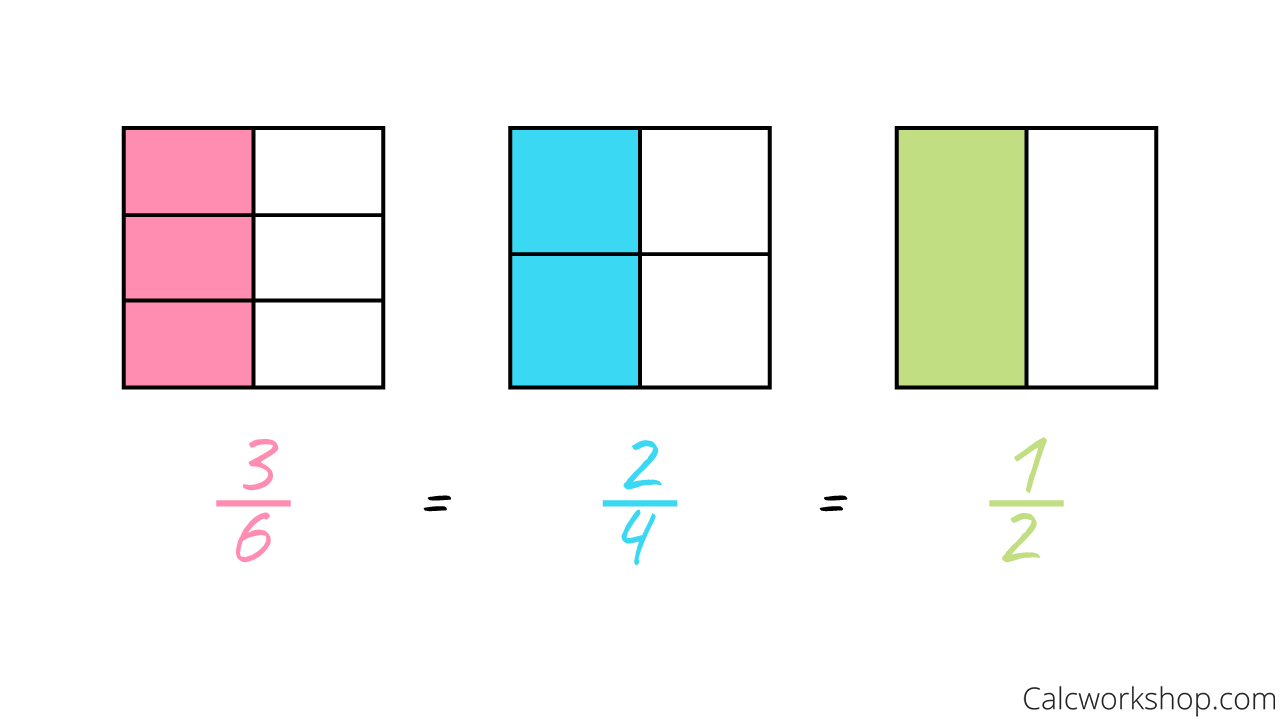
Three Equivalent Fractions — Visual

All three images represent the same part to whole, which indicates that each resulting fraction is equivalent to the other. But what is important to recognize is that while they are equal, only one fraction is in simplest terms — 1/2.

And just as this example indicates, our goal is to transform a fraction by creating an equivalent fraction whose terms no longer have any common factors as noted by Lumen Learning.

So, how do we reduce fractions?

There are two methods:

1. Guess and Check
2. Greatest Common Factor (GCF)

Guess And Check Method

The guess and check method is when we choose a number we know divides evenly into both the numerator and denominator, but we aren’t sure if it’s the largest. So, we may need to continue to reduce the fraction further in necessary.

Worked Example #1

Let’s look at a specific problem.

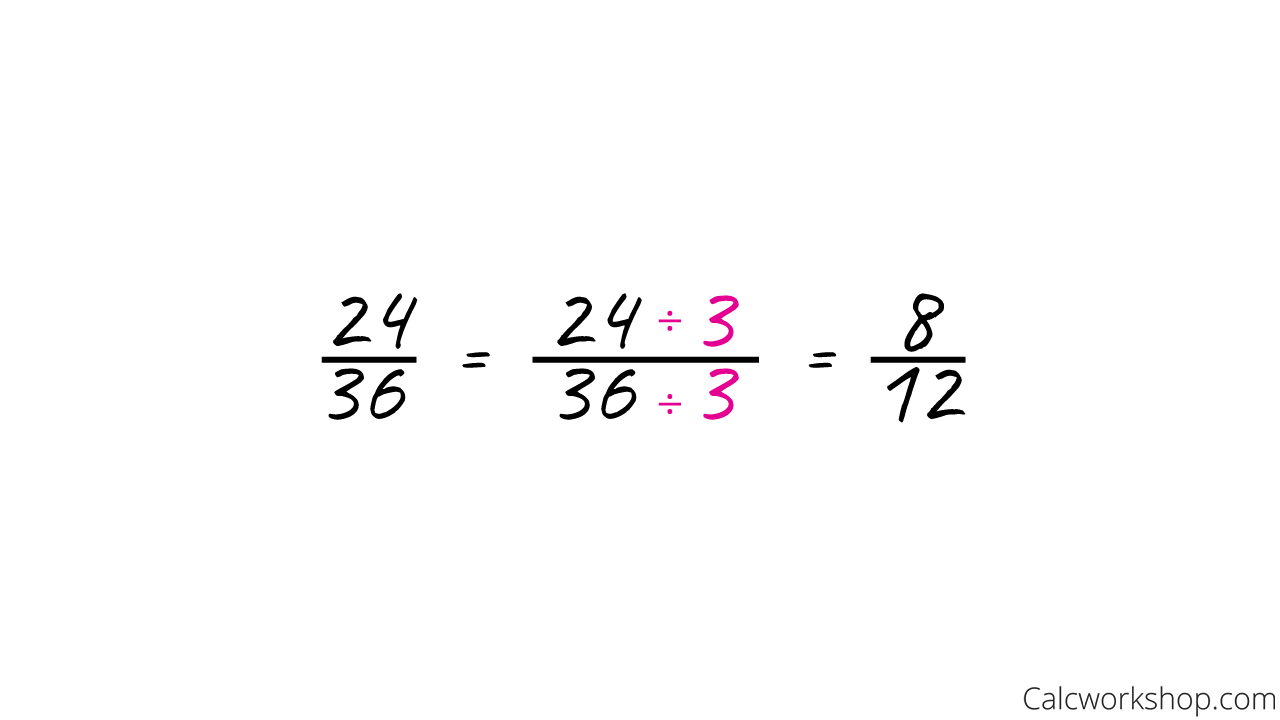
Finding Equivalent Fractions — Example

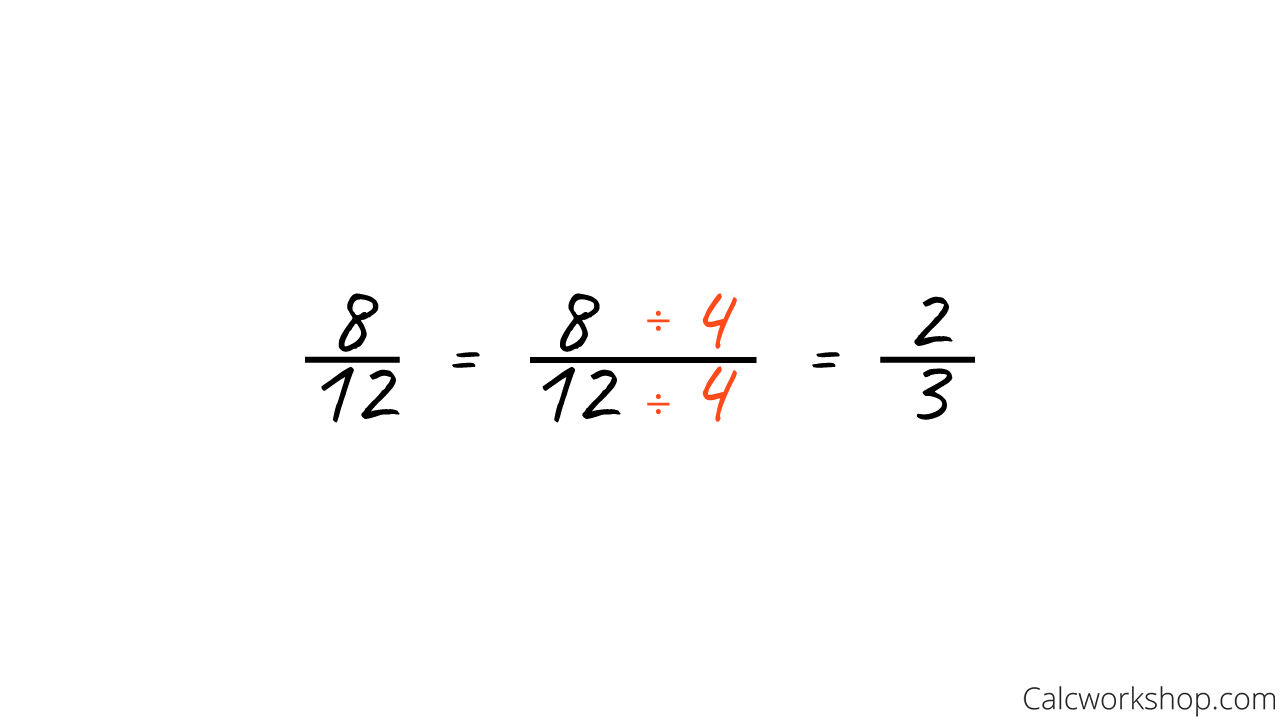
Simplifying Fraction — Example

GCF Method

Whereas the greatest common factor (GCF) method will always give us the largest number for which we should divide.

Worked Example #2

Now, let’s work the same example using the GCF method.

First, let’s use factor trees to find the prime factorization of both the numerator and denominator.

And then we identify the GCF from the prime factorization. Remember, when we find the GCF from a list of prime factors, we choose the fewest of what is common.

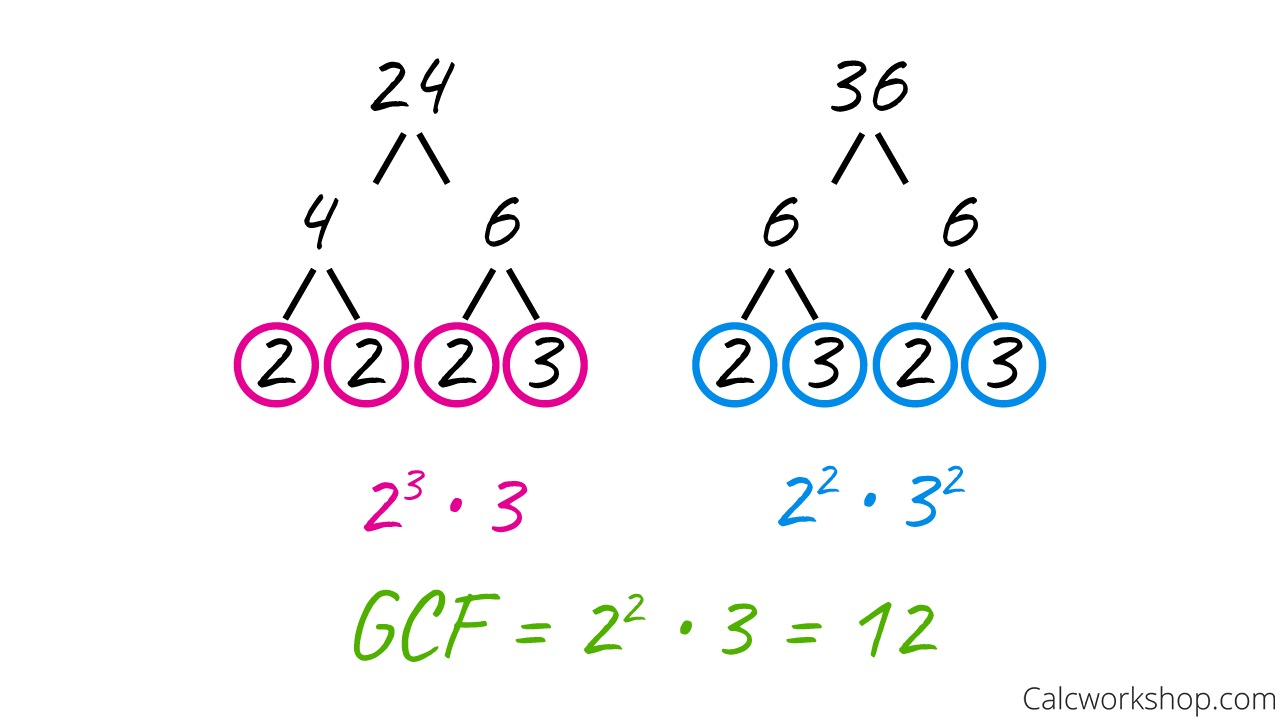
GCF Using Prime Factorization

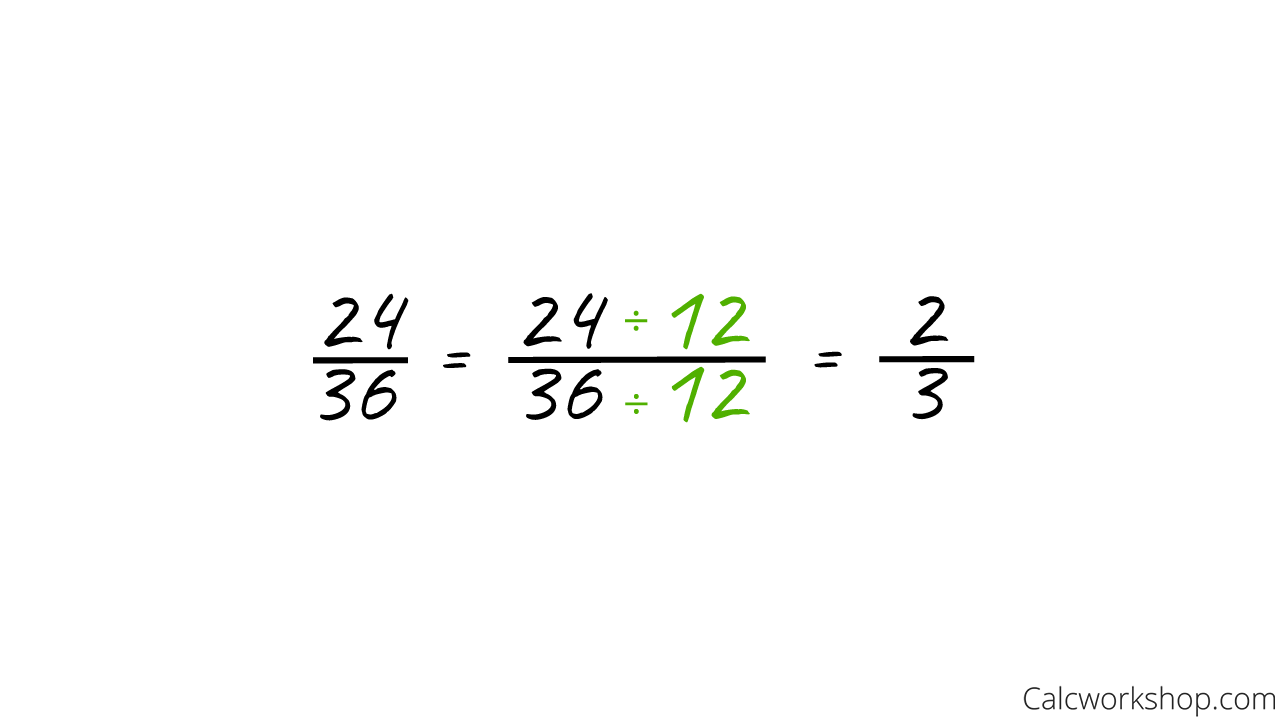
Reduce Fractions To Lowest Term

Worksheet (PDF) — Hands on Practice

Put that pencil to paper in these easy to follow worksheets — test your knowledge!

Simplifying Fractions — Practice Problems
Simplifying Fractions — Step-by-Step Solutions

Final Thoughts

Both methods are perfectly acceptable, and it comes down to personal preference as to which technique you wish to employ.

It is apparent that if your “guess” is also the GCF, you will simplify your fraction fast, as the GCF will always yield the lowest possible reduction.

Throughout this lesson, we will look at numerous examples of how to reduce fractions to simplest form as well as some applications problems where we will first create a fraction and then reduce it to the lowest terms.

Let’s jump right in!

Video Tutorial — Full Lesson w/ Detailed Examples

37 min

• Introduction to Video: Simplifying Fractions
• 00:00:34 – How do we simplify fractions?

• 00:11:29 – Reduce each fraction to simplest terms (Examples #1-6)
• 00:25:34 – Write the fraction from the given table and reduce your answer (Examples #7-8)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions