Did you know that a factor tree is the easiest way to find the prime factorization of a number?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
Let’s jump in and see how this works.
So prime factorization looks at two things:
- Primes
- Factors
Recall that factors are numbers we multiply together to get another number.
Well, prime factorization is all about finding which “prime” numbers multiply together to produce the original number.
What Is A Prime Number?
When only two factors of a number are one and itself, then the number is a prime number.
For example, here is a list of some common prime numbers.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, etc.
What Is A Composite Number?
Now a composite number is a number that has other factors besides one and itself. In essence, composite numbers are numbers other than prime numbers.
But it is important to note that 0 and 1 are not considered prime or composite.
Factor Tree (How-To)
Okay, so now that we remember what prime numbers are, let’s look at the process of finding those prime numbers that multiply together to get the original number. The method we use is called a factor tree as discussed by Math is Fun.
A factor tree is a diagram with branches that we use to go through the factoring steps. The trick to using a tree diagram is to keep factoring until all the dangling “fruits” are prime numbers.
Example #1 — Factors of 18
Let’s look at an example.
Find the prime factorization of 18.
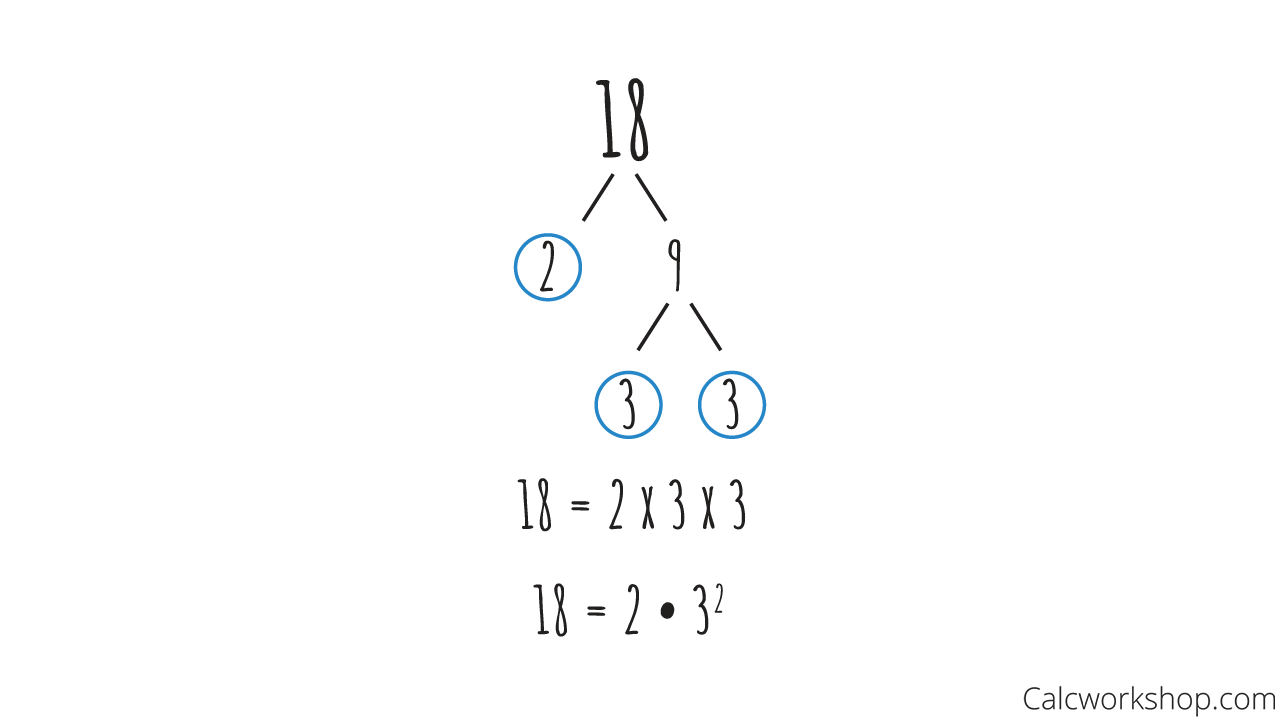
Prime Factorization Of 18
Notice that we only stopped when all of our dangling fruit were prime numbers.
But what would happen if we started with different factors? Does this change the the problem?
Nope!
Let’s prove it.
Suppose instead of starting with 2 and 9 — we started with 3 and 6.
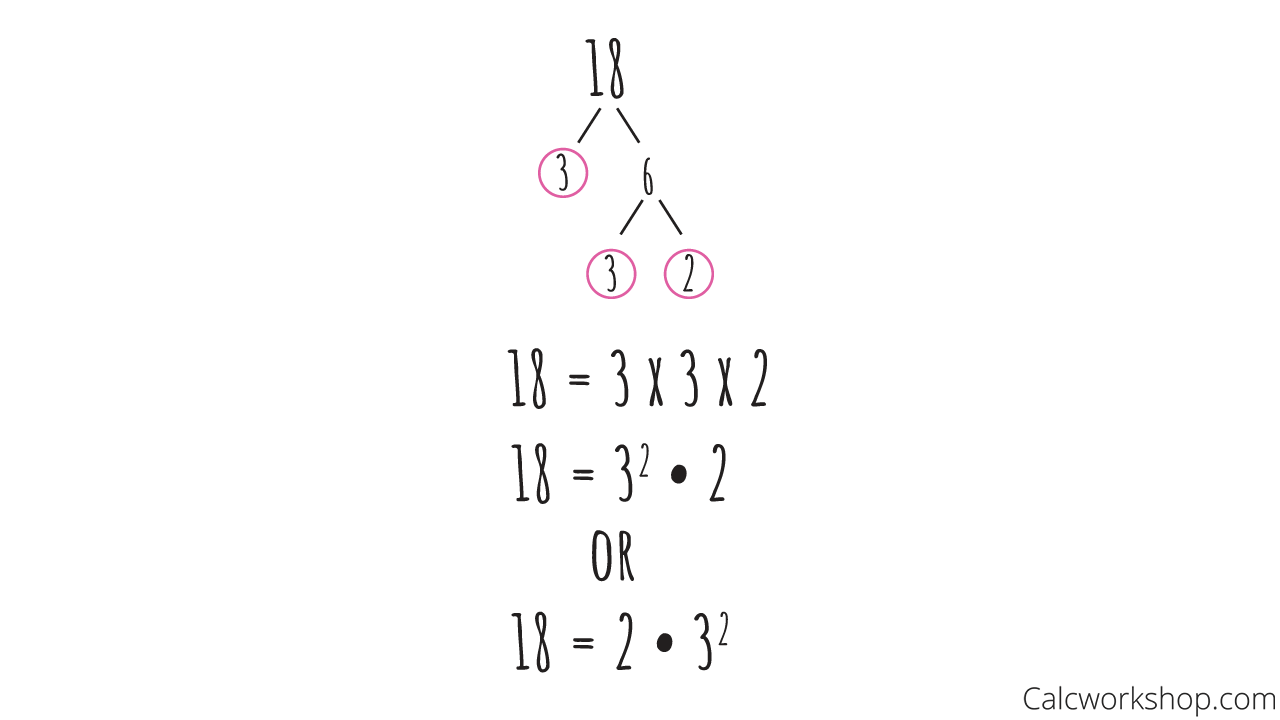
Factor Tree Of 18
See, we arrived at the same answer as before, which means no matter which two factors you start with, you will always arrive at the same prime factors!
Notice that all we do to find our prime factors is to divide our given value by a number that goes in evenly. And the product of all of our prime factors will equal the original value. For example,
Example #2 — Integer Factorization of 96
Let’s look at another example.
Find the prime factorization of 96.
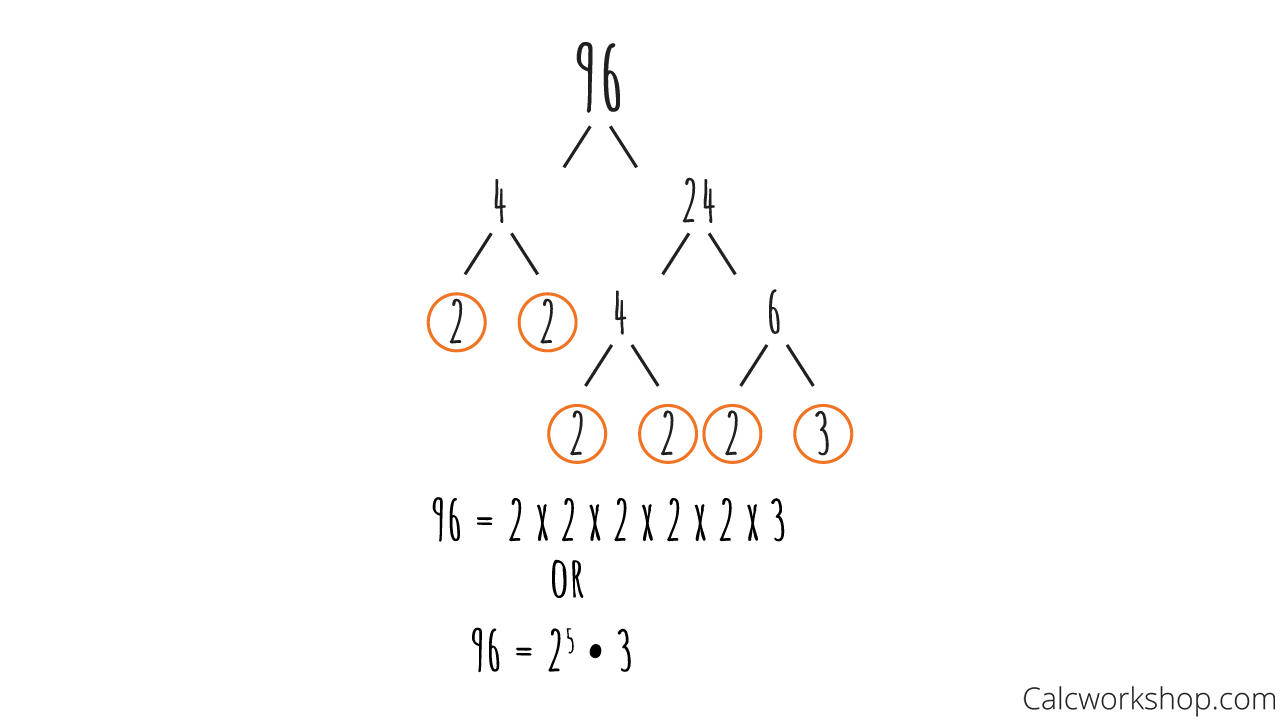
Prime Factorization Of 96
Example #3 — Prime Factorization in Reverse
We will also learn how to take the prime factorization and use it to find the original number by applying the order of operations!
For example, find the original number given the following prime factorization.
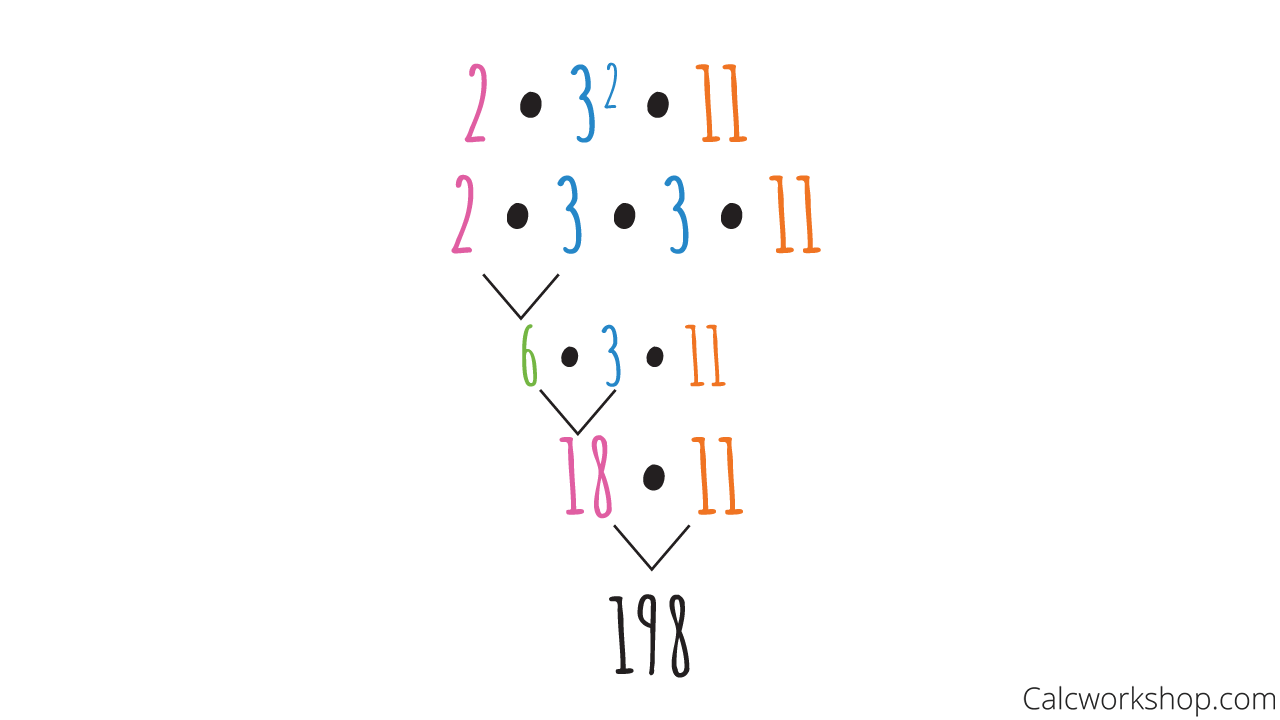
Prime Factorization In Reverse
The Why
But why do we need to find the prime factorization of a number?
What’s the point?
Well, it’s is used when we need to factor polynomials (something we will learn about in Algebra), and it is utilized heavily in code breaking and computer encryption.
Cool!
But for a more practical reason, it’s because we use it when simplifying and combining fractions!
Worksheet (PDF) — Hands on Practice
Put that pencil to paper in these easy to follow worksheets. The handouts are designed so that it doesn’t matter if you’re in 5th, 6th, 7th grade, or beyond — you’ll have everything you need to test your knowledge and learn this material.
Prime Factorization — Practice Problems
Prime Factorization — Step-by-Step Solutions
Video Tutorial — Full Lesson w/ Detailed Examples
You’ll delve into 12 additional explanations and problems with increasing difficulty to enhance your understanding of these techniques. Let’s go!
36 min
- Introduction to Video
- 00:00:31 – What are factors? Prime and Composite Numbers? and How to use a factor tree?
- 00:12:14 – Find the integer factorization for each number (Examples #1-6)
- 00:22:52 – Find the prime factorization (Examples #7-10)
- 00:32:23 – Use reverse factorization to identify the original number (Examples #11-12)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.