Did you know that the least common multiple, or LCM, is the smallest positive multiple that is common to two or more numbers?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
But first, what is a multiple, and how is it different than a factor?
Let’s look at an example.
List the multiples and factors of 6.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, …
- Factors of 6: 1, 2, 3, and 6
So, factors are the integers we multiply together to get the original number.
And multiples are all the integers that 6 can go into.
That means, whenever you see the word “multiple” you want to think multiply!
- 6 = 6 x 1
- 12 = 6 x 2
- 18 = 6 x 3
- 24 = 6 x 4
- Etc.
How do we find the least common multiple?
Well, just like we saw with finding the greatest common factor, there are actually two techniques for identifying the LCM:
- Listing
- Prime Factorization
Using our listing method, we will work L-C-M backward:
- M: List multiples for each number
- C: Identify common multiples
- L: Choose the lowest multiple (smallest number they have in common)
And for the prime factorization method, we will create a factor tree and identify each number’s prime factors. Then we will select all factors, always choosing the largest common factor.
List Method
The listing method, sometimes called the roster method, is simply a listing of multiples. When we learned to multiply we employed a technique called skip counting to help us recognize equal groups, and that’s basically what we are doing here — we’re going to skip count by each integer given.
For example, let’s find the least common multiple of 6 and 10 using both techniques.
First, we will use the listing method by “skip counting” and select the lowest integer they both have in common.
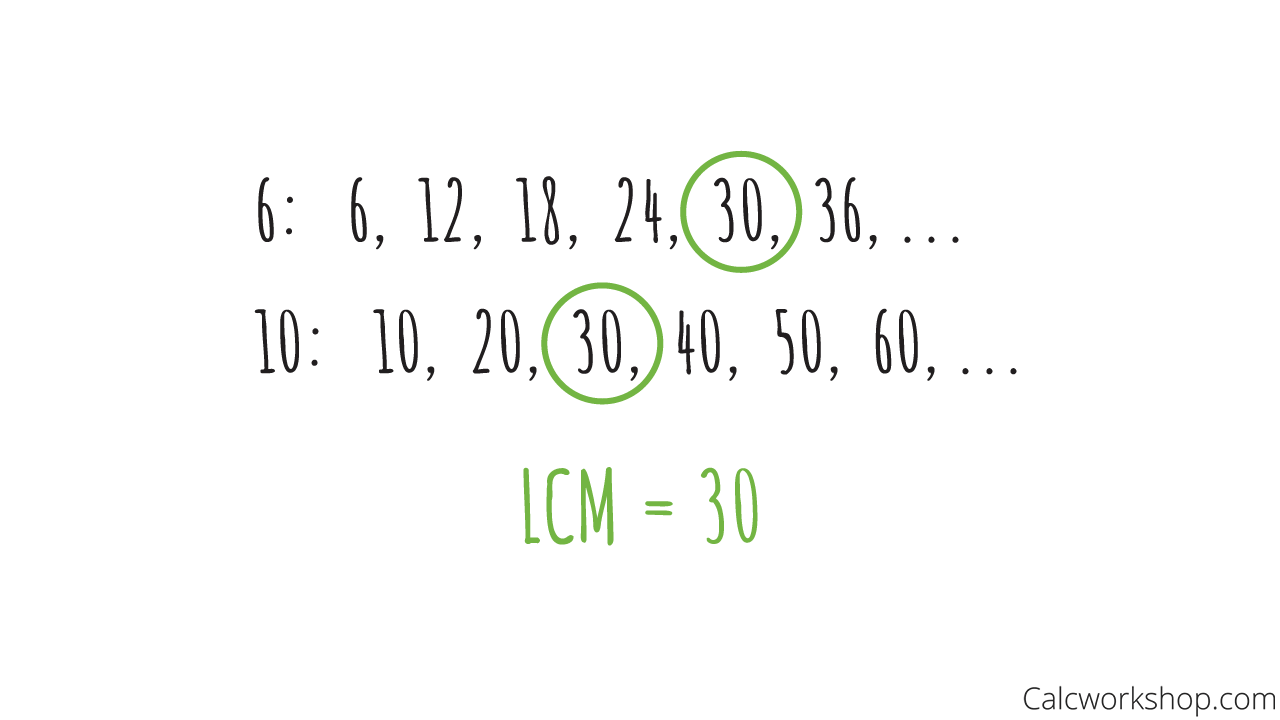
Find The LCM of the Numbers Using Lists of Multiples
Prime Factorization Method
Now, let’s see how to use the prime factorization method. For this technique, we create factor trees for each integer as seen below, and then multiply the largest of all prime values found in both trees.
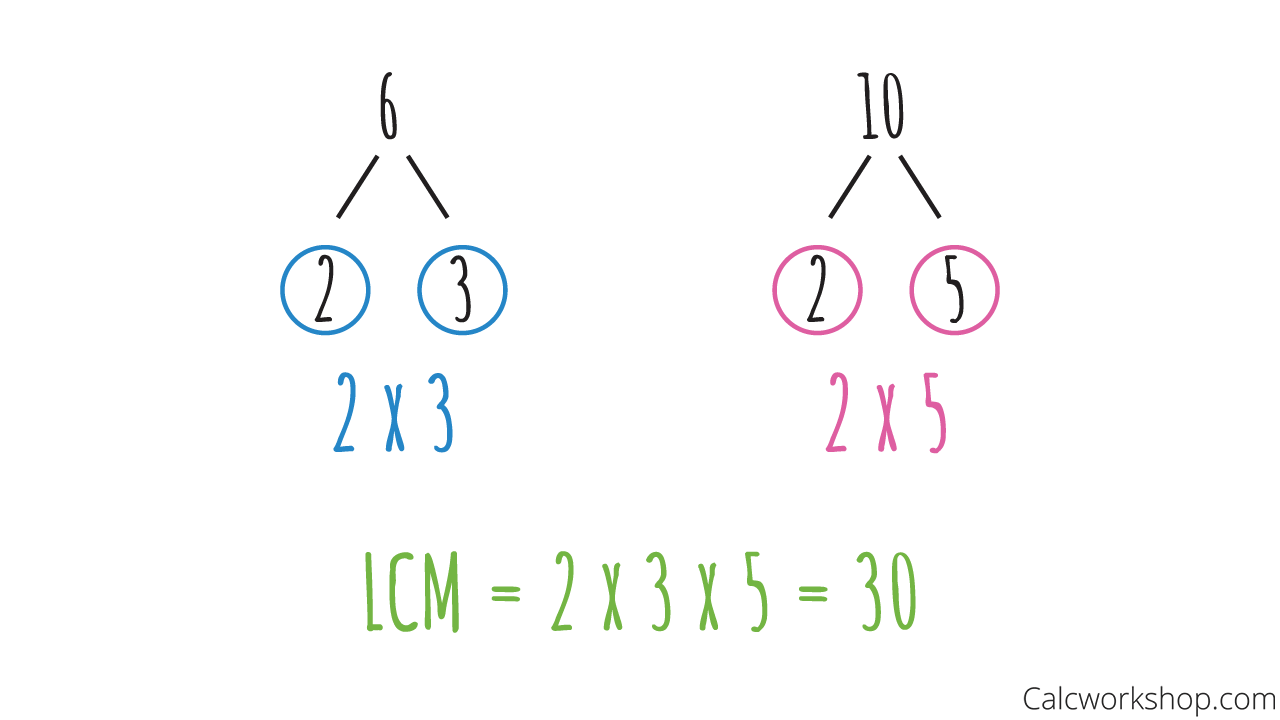
Prime Factorization of 2 Numbers
Method Summary
Here’s a breakdown of the two methods for identifying the Least Common Multiple:
- When we list factors, we choose the LOWEST common number.
- When we use prime factorization, we choose MORE – most power from each factor.
As you have probably noticed, the first method is easier to use, as all we’re doing is multiplying (i.e., skip-counting) and selecting the lowest number.
But this method is not very practical for integers bigger than 12, whereas the prime factorization method is tried and true and will work for any integer as noted on the Art of Problem Solving.
Example — Hard LCM Problem
Let’s look at another example, where using prime factorization really shows itself to be the best method for discovering the least common multiple
Find the LCM of 8 and 42.
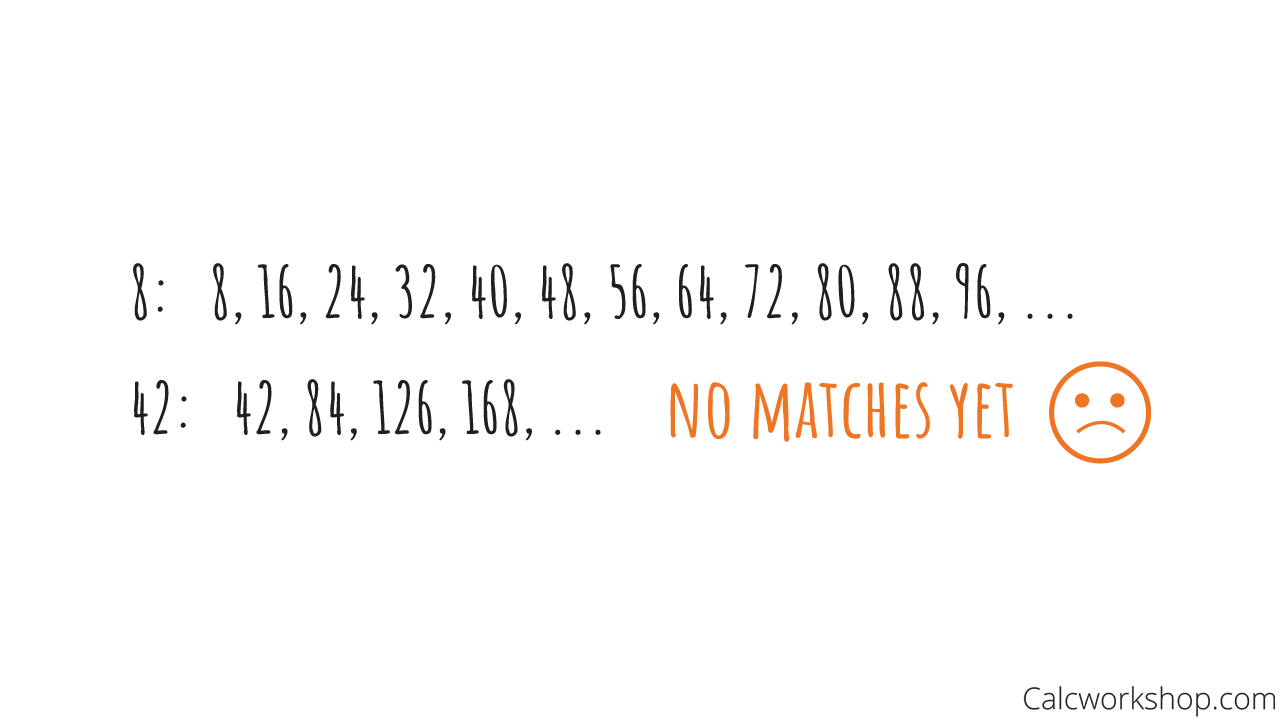
LCM of 42 and 8 — Example
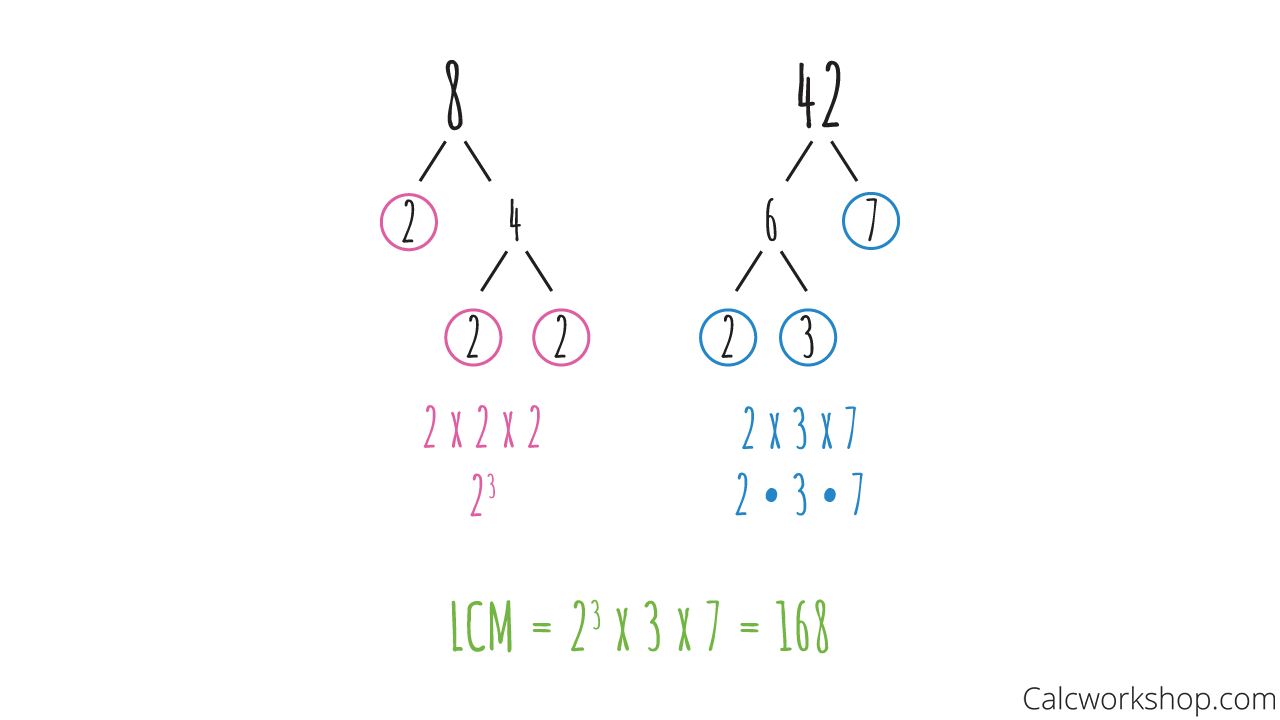
LCM Using Prime Factorization
As you can see, prime factorization helped us to locate the LCM much faster than skip-counting.
Example — LCM Of Three Numbers
What about finding the LCM for three numbers?
Like we saw with the example above, the method we should employ when discovering the least common multiple for three numbers is prime factorization.
For example, let’s find the LCM of 90, 120, and 300
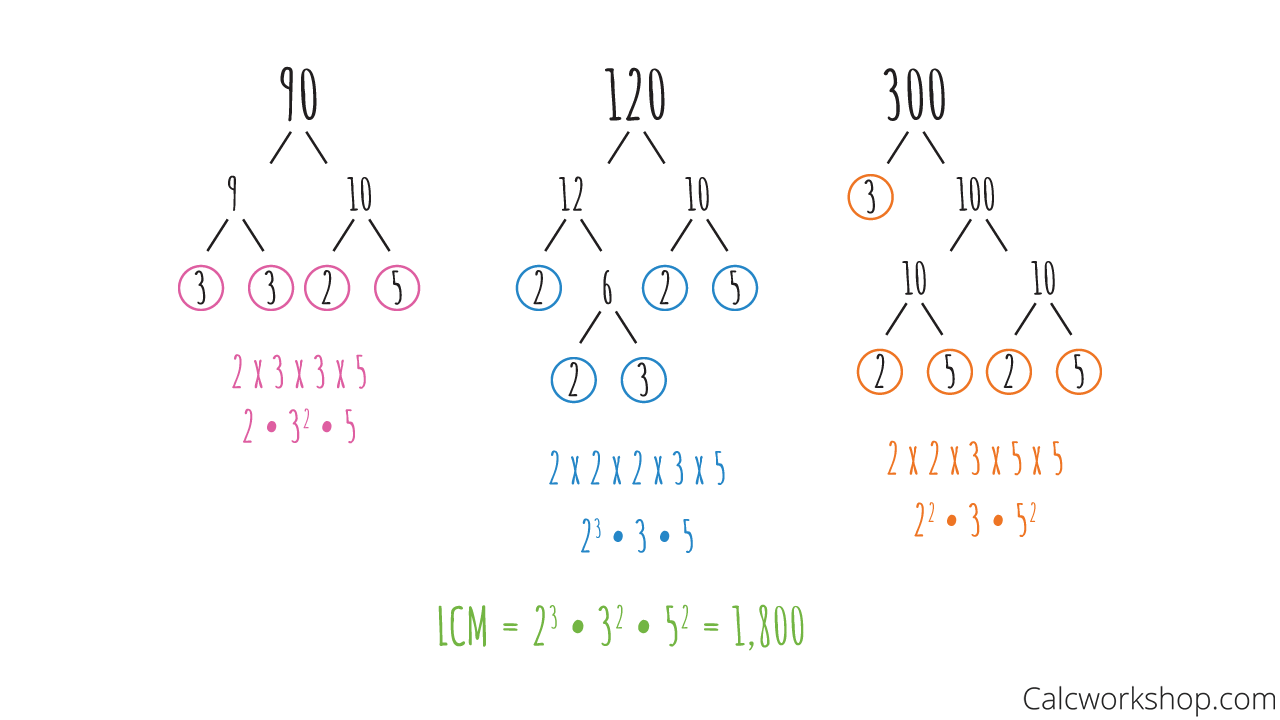
How To Find LCM of 3 Numbers Using Prime Factorization
Trying to list multiples for these three numbers would have been incredibly tedious. Aren’t you glad we just used prime factorization!
Worksheet (PDF) — Hands on Practice
It’s all fun and games until you try it on your own. So give these worksheets a go — and improve your knowledge!
Least Common Multiple — Practice Problems
Least Common Multiple — Step-by-Step Solutions
Video Tutorial — Full Lesson w/ Detailed Examples
Together we will look at various examples of finding the least common multiple and ensuring that we can employ both methods (listing and prime factorization) with success.
37 min
- Introduction to Video: Least Common Multiple
- 00:00:29 – How do you find the LCM?
- 00:08:02 – Determine the LCM using both methods (Examples #1-2)
- 00:13:02 – Find the least common multiple for two or three numbers (Examples #3-8)
- 00:30:03 – Uncover the LCM for three numbers using prime factorization (Examples #9-10)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.