Did you know that all we have to do to find the greatest common factor is work the phrase GCF backwards?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
But first, let’s define our terms.
Greatest Common Factor (GCF) — the largest number that divides evenly into each number in a given set of numbers.
And there are two ways we can find these factors, and they both involve using the letters G-C-F?
Let’s shine a light on this with some examples…
Factor Pairs — In Action
So, let’s find the GCF of 12 and 18 using our two techniques.
Our first method is to list factor pairs. We do this by working G-C-F backward.
- F: List factors or factor pairs
- C: Identify common factors
- G: Choose the greatest common factor
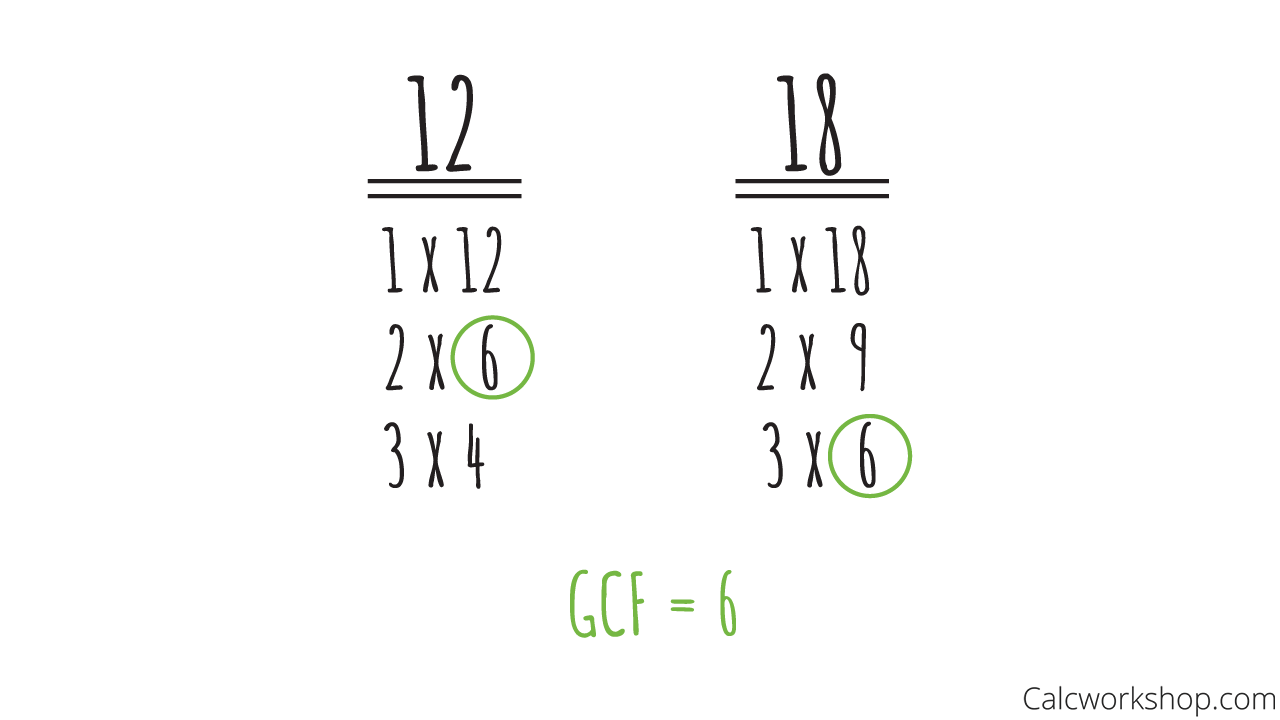
Factor Pairs of 12 and 18
Notice that the largest number they both have in common is 6 — therefore, the GCF for these two numbers is 6.
But this technique is not foolproof, as it only works if you do identify every factor for each number. The tried and true method is to use the prime factorization method.
GCF Using Prime Factorization
Once again, we will use the letters from G-C-F to help us out. We will identify all the common factors, but instead of choosing the greatest, we will be selecting the fewest common numbers.
Again, this is better seen in an example.
So, let’s find the GCF of 12 and 18, but we will use the prime factorization method. This technique asks us to list all the prime factors for each.
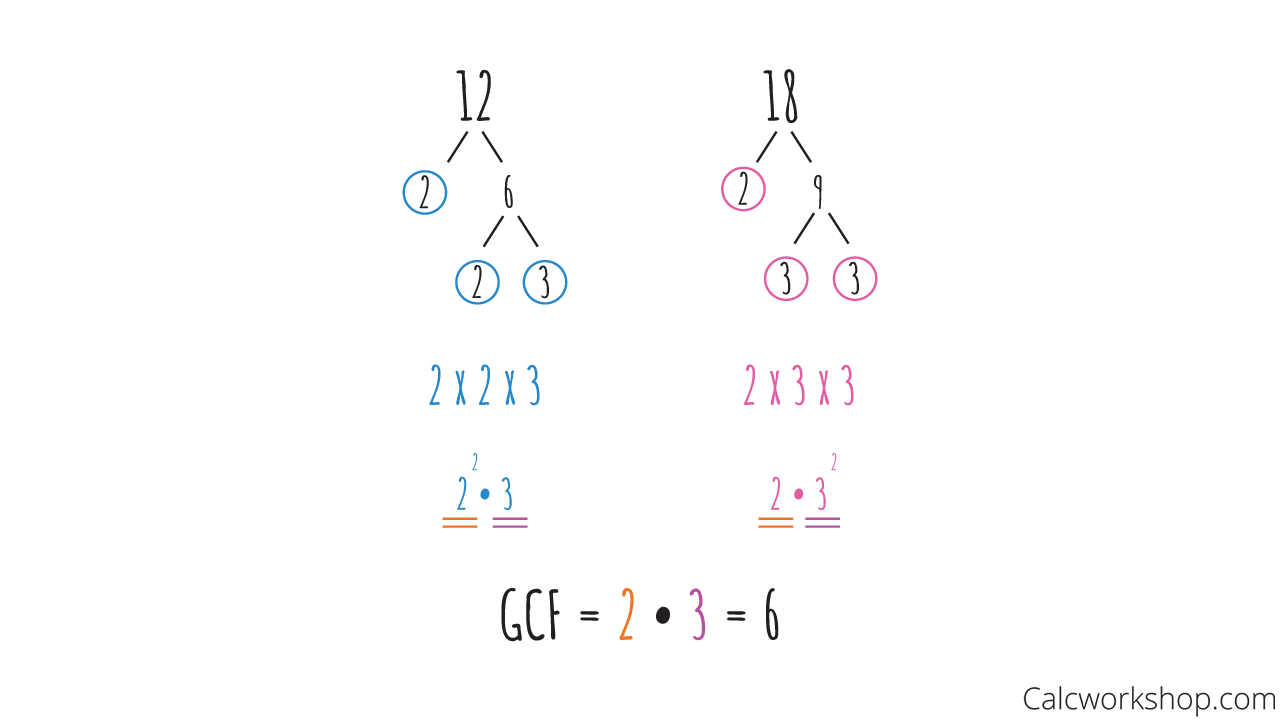
GCF of 12 and 18
The GCF is found by identifying those numbers they have in common, and then selecting from those common numbers, which are the smallest — choosing the fewest they have in common as mentioned on Purple Math.
What is important to note, is that both techniques (listing factors or prime factorization) gave us the same answer of 6 as the greatest common factor for 12 and 18. So, it really comes down to personal preference as to which method you want to use, and also the numbers that you are given to work with.
What you will find is that the first method tends to be significantly faster than the second method. But as previously stated, the second method will always work.
Here’s a breakdown of the two methods:
- When we list factors, we choose the GREATEST factor in common.
- When we use prime factorization, we choose the FEWEST common factors.
Example — GCF of Three Numbers
Let’s look at another example, finding the greatest common factor of three numbers, showing both methods.
Method #1
Find the GCF of 32, 48, and 64 by listing factors or factor pairs.

Greatest Common Factor of 32 — 36 — 64
Method #2
Find the GCF of 32, 48, and 64 by using prime factorizations.
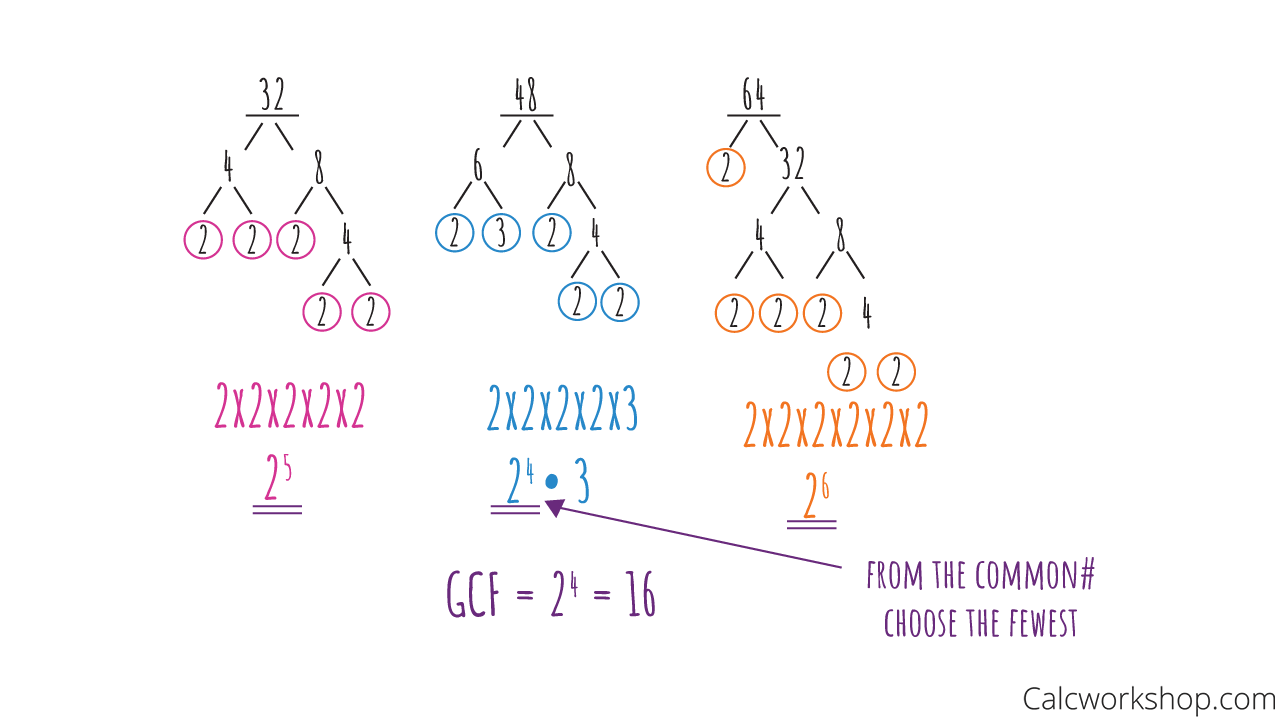
Prime Factorization and GCF of 32 — 48 — 64
Notice, once again, that both techniques gave us a GCF of 16.
What’s important to note is that in Algebra, we will utilize both methods simultaneously when factoring polynomials. When factoring numerals (i.e., numbers), we tend to use the first method of listing factor pairs. But when we factor variables, where we deal with exponents, we utilize the prime factorization method.
So, knowing and being able to use both methods for finding the GCF is invaluable. And it’s the secret sauce for simplifying fractions too!
Worksheet (PDF) — Hands on Practice
Put that pencil to paper in these easy to follow worksheets — expand your knowledge!
Greatest Common Factor — Practice Problems
Greatest Common Factor — Step-by-Step Solutions
Video Tutorial — Full Lesson w/ Detailed Examples
In the video below, we will expand on these concepts, with additional examples increasing in complexity.
42 min
- Introduction to Video
- 00:00:26 – What is the GCF? How do we find the GCF?
- 00:08:26 – Identify the GCF using both methods (Examples #1-2)
- 00:15:33 – Determine the GCF of two numbers (Examples #3-4)
- 00:22:23 – Discover the greatest common factor of three numbers
- 00:28:16 – Use the listing factor or prime factorization to solve the problem (Examples #7-9)
- 00:39:00 – Find the greatest common factor of three variables (Example #10)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.