Keep — Change — Flip, the simple 3 step process for dividing fractions.
But first, let’s learn the ground rules.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The key to dividing fractions lies in the power of reciprocals!
What Is A Reciprocal
A reciprocal, sometimes called the multiplicative inverse, is the transpose of the numerator and the denominator.
All this means is that we flip the fraction so that the numerator becomes the denominator and the denominator becomes the numerator.
For example:
- The reciprocal of 1/5 is 5/1, or in other words, the multiplicative inverse of 1/5 is 5.
- And the reciprocal of 3/7 is 7/3.
But why do we care about reciprocals?
We care because it helps us to create the identity property. In other words, when a number is multiplied by its reciprocal, it will always equal one!
For example, if we multiply 3/7 and 7/3, we get 21/21, which is one whole!
Throughout this lesson, we will notice that the reciprocal of a whole number will always be a unit fraction. The multiplicative inverse of a mixed number will always be a proper fraction.
Cool!
Reciprocals the key to the division of fractions because the only operations we are allowed to perform on fractions are:
- Addition
- Subtraction
- Multiplication
NOT Division.
Therefore, we have to have a way to transform division into its inverse operation of multiplication, and the way we do that is by flipping our fraction!
Area Model
Before we get to the steps, let’s see a visual representation of how diving fractions work by looking at an area model.

How To Draw a Model for Dividing Fractions
And as we saw with multiplication, while an area model illustrates the division process, it’s not always practical to use.
Thankfully there are some easy to follow steps for how we divide fractions!
- If necessary, transform all mixed numbers or whole numbers into improper fractions.
- Keep the first fraction the same.
- Change the division symbol to multiplication.
- Take the reciprocal of the second fraction.
- Reduce and Multiply.
Keep — Change — Flip
Here’s an easy way to remember this: Keep (leave the first fraction the same) — Change (change the division symbol to multiplication) — Flip (take the reciprocal of the second fraction)
To help, let’s shine a light on a few problems.
Example #1
Consider the following problem, where we want to divide three-fifths by two-sevenths.
First we apply keep-change-flip!
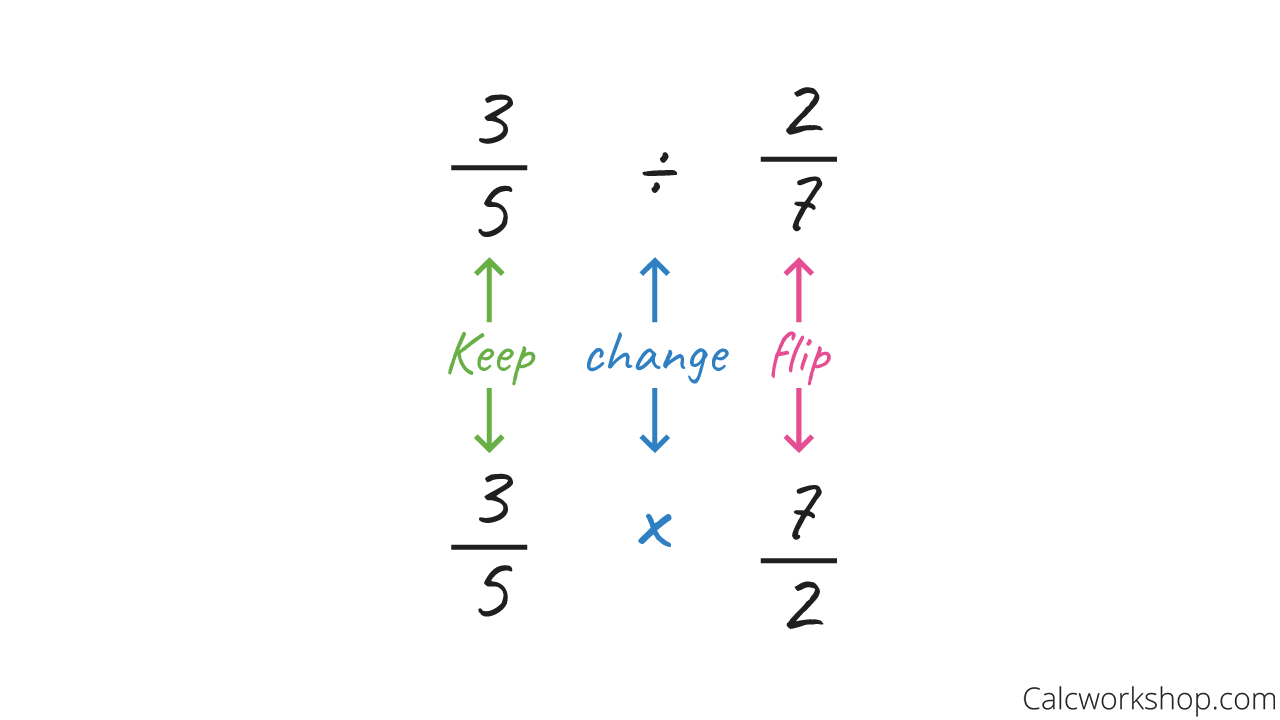
Keep Change Flip (Division of Fractions)
Now, we will evaluate our numerical expression by multiplying the first fraction of three-fifths by the reciprocal of the second fraction.
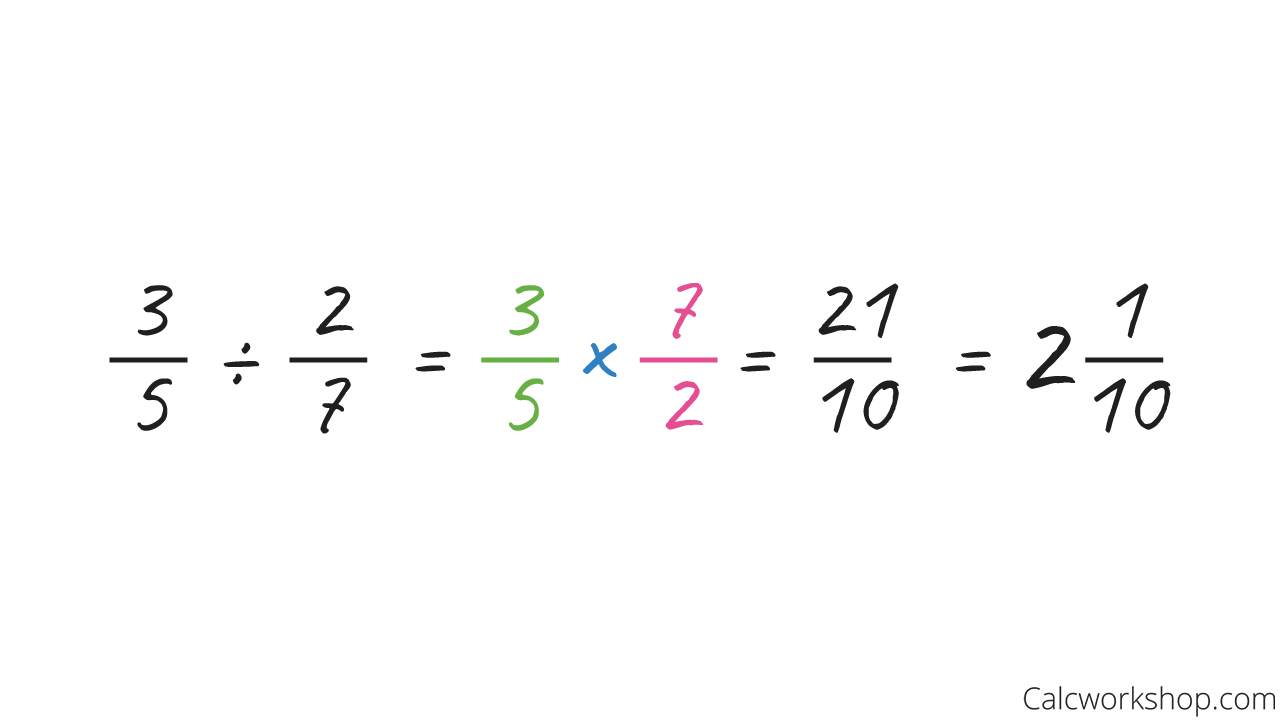
How To Divide Two Fractions
So, our answer is twenty-one tenths or two and one-tenth.
That’s it!
Example #2
We will also see that our rules for multiplying fractions will come in handy as well, because after transforming our division problems as noted on the Prodigy blog, we will want to reduce our fractions before we multiply.
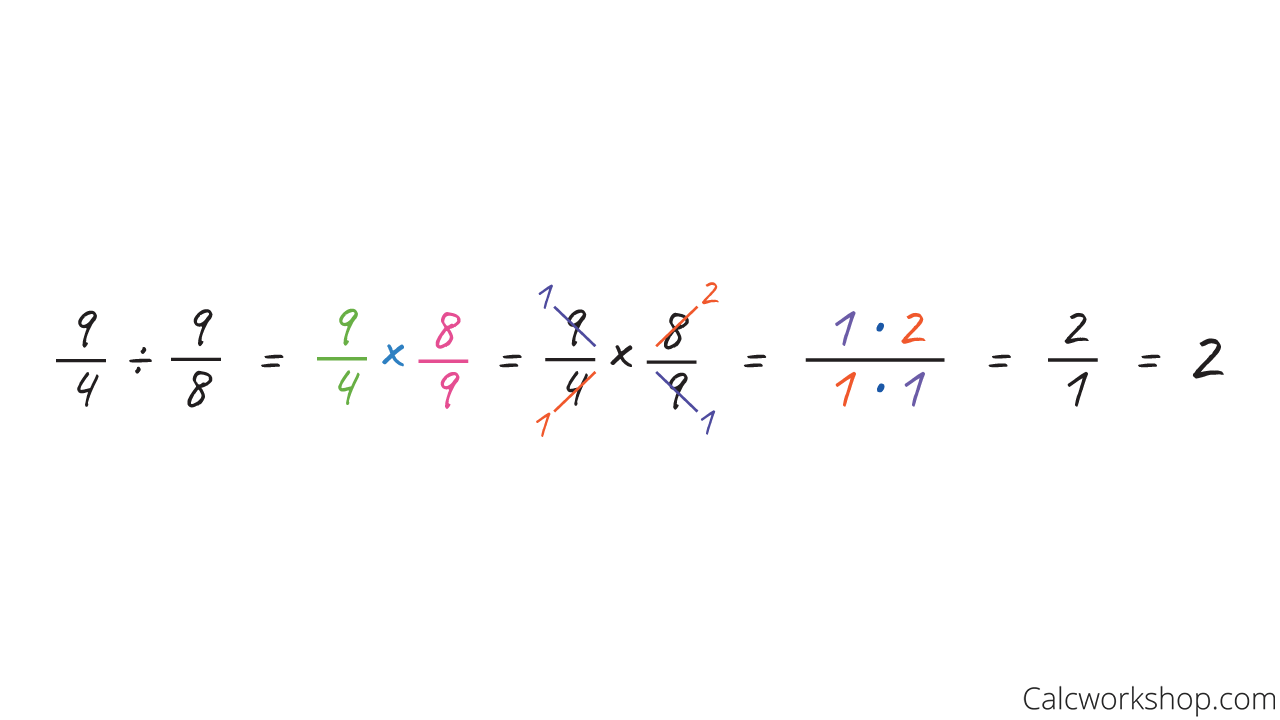
Cross Reduce
Example #3
We will also investigate how to divide fractions and mixed numbers!
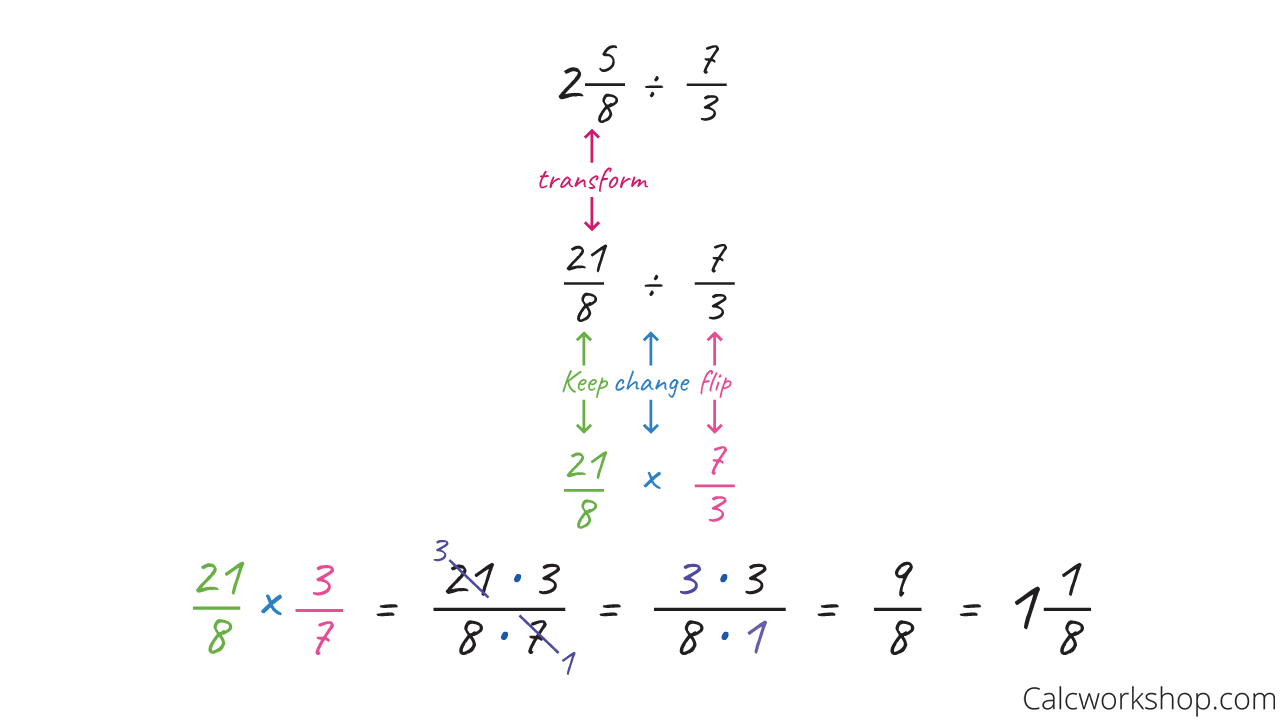
Dividing Mixed Fractions
Worksheet (PDF) — Hands on Practice
Put that pencil to paper in these easy to follow worksheets — expand your knowledge!
Dividing Fractions — Practice Problems
Dividing Fractions — Step-by-Step Solutions
Summary
In this video lesson below, you’ll learn how to solve various types of fractions including:
- Proper
- Improper
- Mixed Numbers
You’ll see how reciprocals and GCF combine to make this an easy step-by-step process.
Trust me!
The steps are clear and straightforward, and you’ll get the hang of it in no time.
Let’s go!
Video Tutorial — Full Lesson w/ Detailed Examples
58 min
- Introduction to Video
- 00:00:35 – Finding reciprocals and area models for division (Examples #1-6)
- 00:13:08 – How to divide fractions (Examples #7-10)
- 00:25:20 – Division with complex fractions (Examples #11-12)
- 00:32:00 – Solving mixed numbers (Examples #13-17)
- 00:44:28 – Split the fractions (Examples #18-19)
- 00:48:27 – Divide three fractions (Example #20)
- 00:53:40 – Perform the indicated operation with three fractions (Example #21)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.