Decimal to Fraction
Simple How-To w/ 21+ Examples!

Did you know that converting decimals to fractions is a simple 3 step process?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

It’s true!

So, if you need help with fractions and decimals — you’re in the right place.

Let’s go!

Key Terms — Quick Run Through

Fractions use the “fraction bar” to separate the part (numerator) from the whole (denominator).

In contrast, a decimal expresses the part as place values to the decimal point’s right, and the whole is the place values to the left of the decimal point.

So, knowing how to convert back and forth is an important skill.

How To Convert A Decimal To A Fraction

1. Read it!
2. Write it!
3. Reduce it!

Yes! It is as simply as that.

They key is to remember your place value chart, so that you can read any decimal value. This will give you a much-needed clue as to how write a decimal as a fraction (part over whole). And all that’s left is to reduce (simplify)!

Let’s work through a few examples to see these three steps in action!

Example #1 — 0.9 As A Fraction

Okay, so suppose we wish to express 0.9 as a fraction. All we have to do is “read” our decimal and “write” it in words, and then “reduce” the fraction to simplest terms.

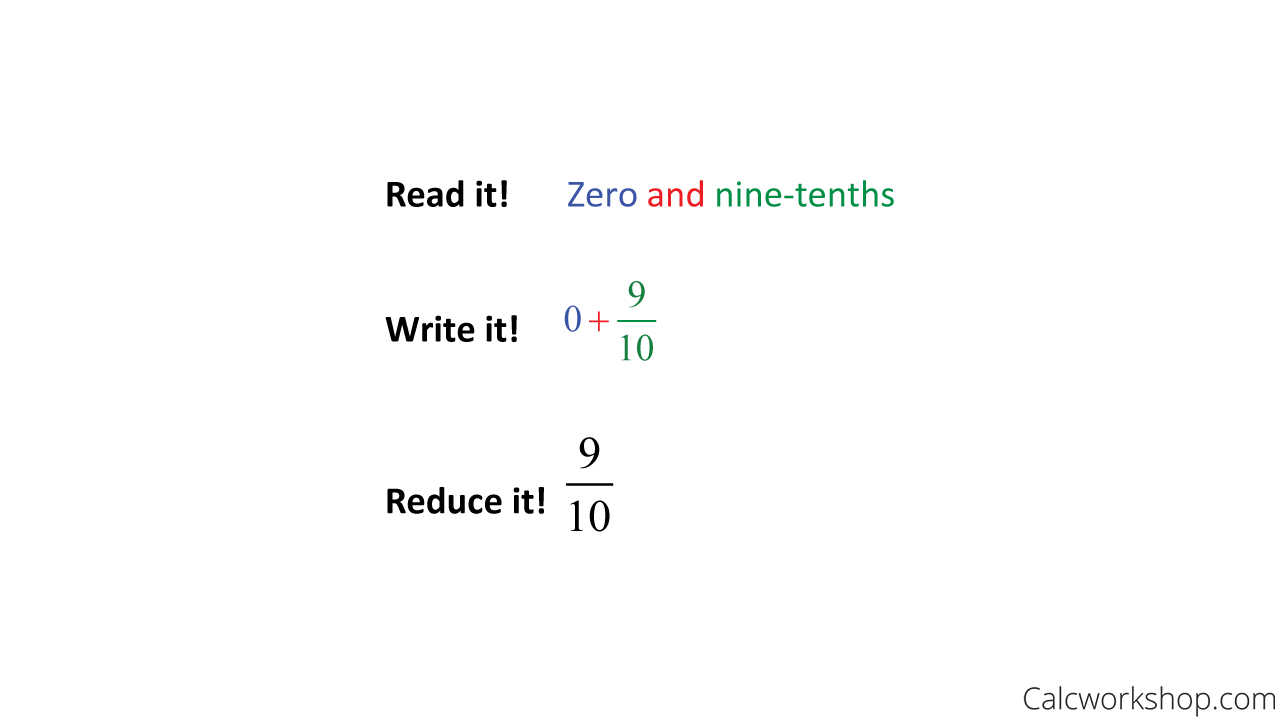
0.9 as a Fraction in Simplest Form

Example #2 — 0.02 As A Fraction

Looking at another example, let’s consider the decimal 0.02. We change the decimal to a fraction using our three steps: read — write — reduce.

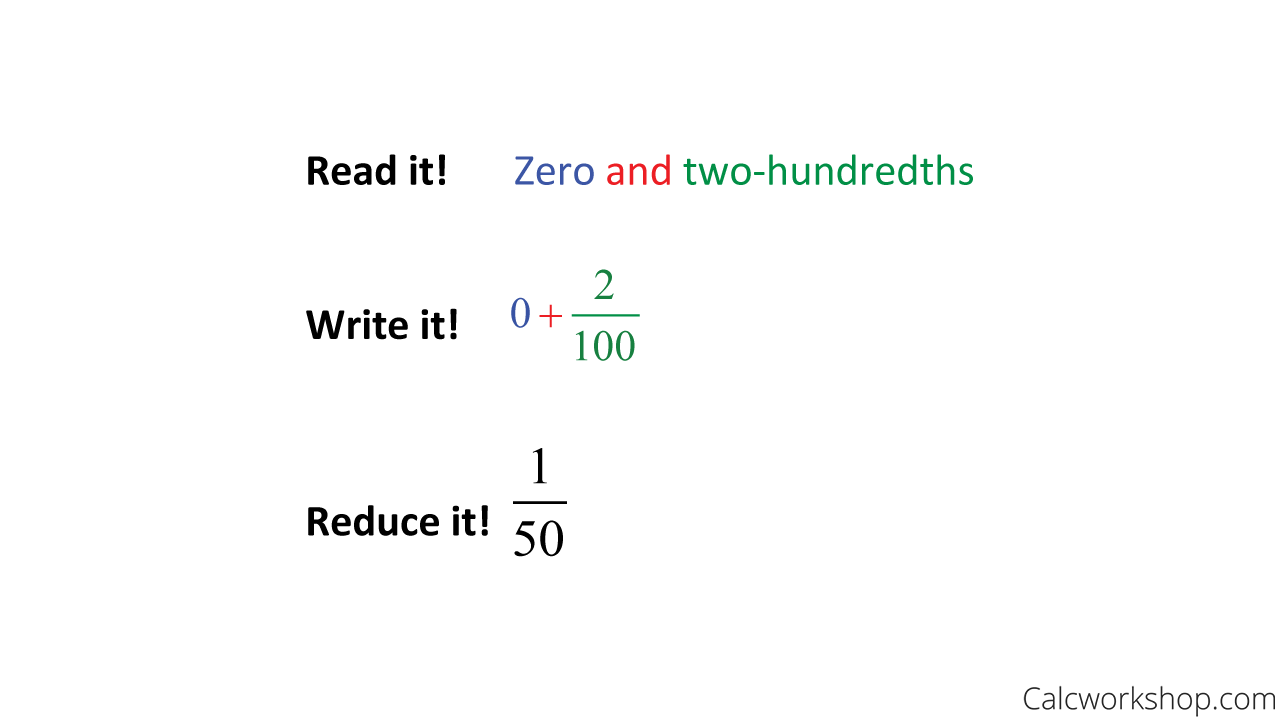
Convert .02 Decimal to Fraction

Example #3 — 5.086 Into A Fraction

Now it’s time to look at a decimal that has both a whole number part and a decimal part. The steps are exactly the same as before, we read our number, write it in words and reduce. Recall that the keyword “and” tells us to add the whole number and the resulting fraction together to create a mixed-number fraction, as seen below.

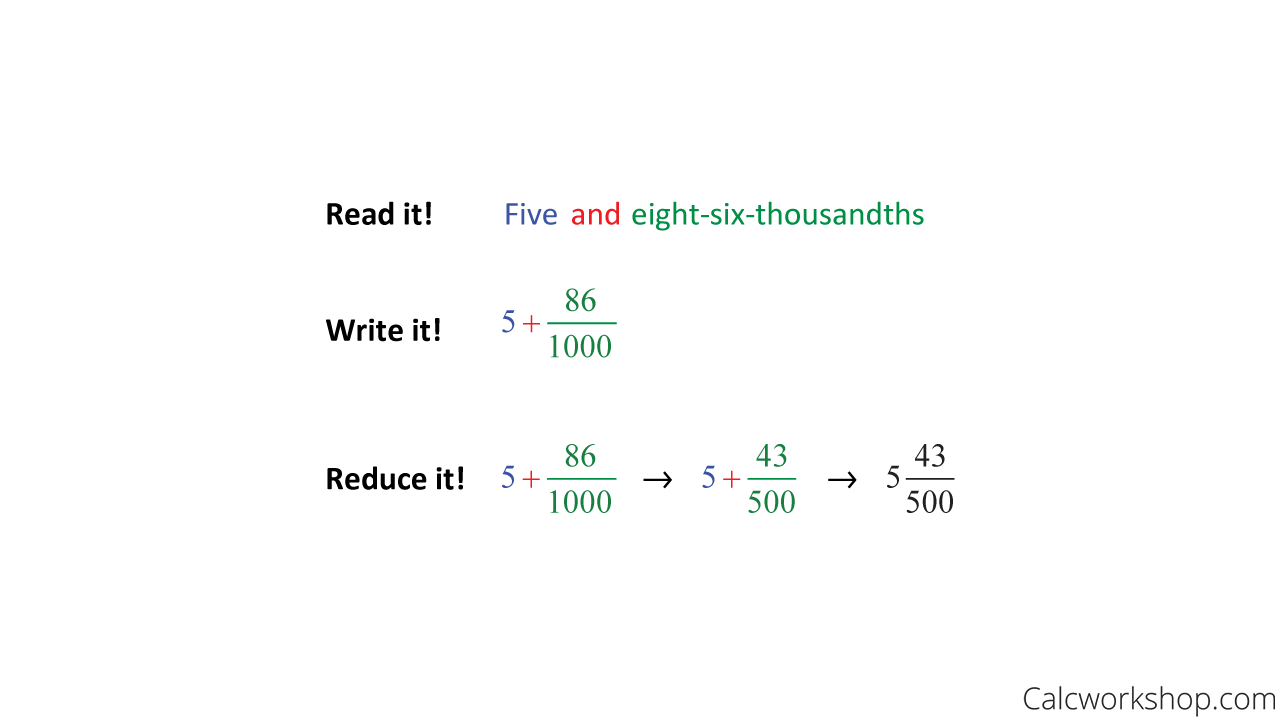
How to Make a Mixed Number into a Fraction

See, all you have to do is Read—Write—Reduce!

How To Turn A Repeating Decimal Into A Fraction

But what about recurring decimals?

This will involve a bit of manipulation, as we will need to set up two equations to find our result. But don’t worry, the steps are straightforward and simple to follow.

Steps

1. First, we create an equation where we let x equal the decimal number.
2. Second, we count the number of decimal places you will need to move the decimal to the right to create a whole number from the repeating terms.
3. Third, we create another equation where we multiply both sides of our first equation by a factor of 10 and the number of decimal places we counted in our second step.
4. Fourth, we subtract the two equations and solve for x.
5. And lastly, we reduce our fraction.

Wait a minute — This seems kinda difficult!

That’s exactly why we’re going to shine a light on these steps with two problems, so you’ll understand the complete process in detail.

Example #1 — 0.4 Repeating As A Fraction

Consider the repeating decimal 0.44444…

Because this decimal does not terminate we can’t apply the same rules of read — write — repeat. Instead, we follow the procedure listed above, as the image below shows in detailed steps.

Correct 0.4 in Fraction Form

Example #2 — Two Digit Repeating Decimal Into A Fraction

Consider the repeating decimal 0.545454…

Just like the example above, this decimal does not terminate, as we see digits repeating. But what makes it different is that we have two repeating decimals instead of one. The good thing is that the process for converting a repeating decimal into a fraction doesn’t change, the only difference is the factor of 10 in step three will increase, as indicated below.

Correct How to Make Two Repeating Decimal a Fraction

In the video tutorial that follows, you’ll learn how to work through countless examples like the ones seen above and understand how to deal with repeating decimals when the “repeating part” starts later in the decimal answer, such as 0.2349999.

You can also review Dr. Knott’s resource on decimals for further exploration too.

How To Add Fractions With Decimals

So, now we know how to transform decimals into fractions, but why is this useful?

Because there will be times when you will be asked to add, subtract, multiply, or divide fractions and decimals – meaning we will have to translate them back and forth before you can perform the operation.

Or you may need to compare the numbers using inequality symbols.

Let’s take further look.

Example — Mixed Types

For example, let’s find the sum of 2/9 and 0.3

Change the Decimal to a Fraction

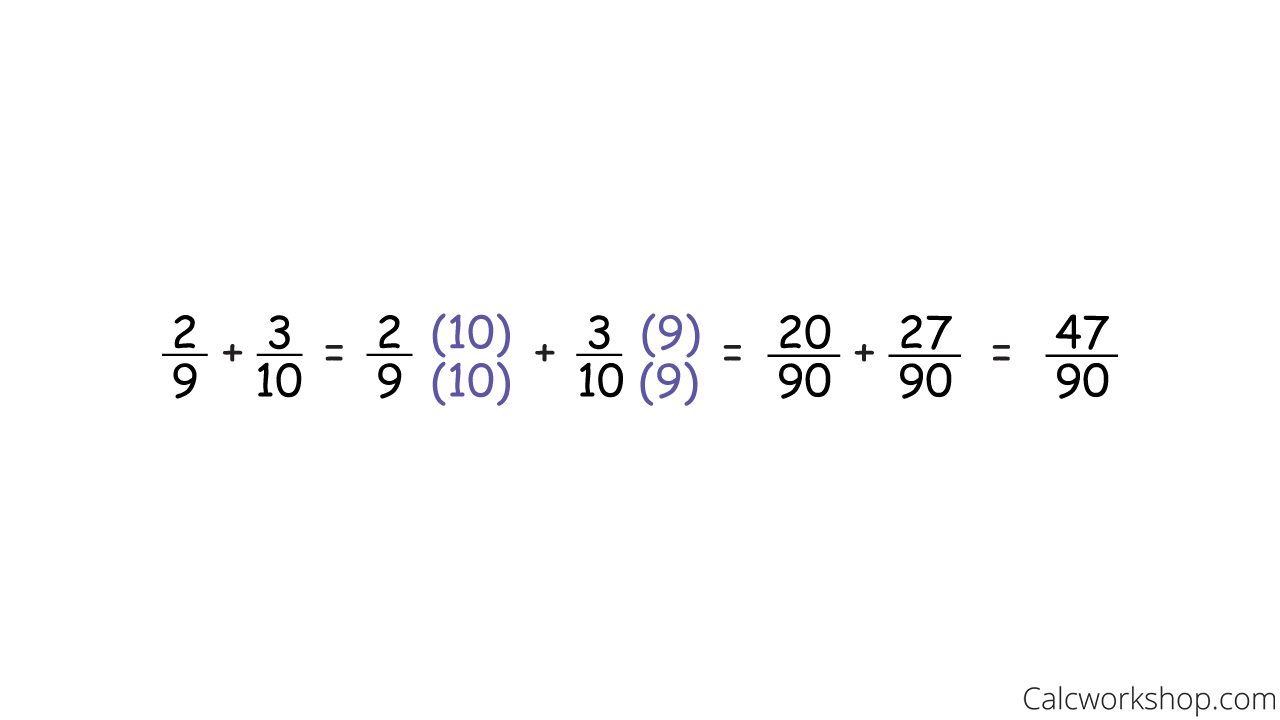
Adding Unlike Fractions

Now that’s pretty handy!

Worksheet (PDF) — Hands on Practice

Put that pencil to paper in these easy to follow worksheets — expand your knowledge!

Decimal to Fraction — Practice Problems
Decimal to Fraction — Step-by-Step Answer Key

Closing Thoughts

Now you have an overview along with some step-by-step examples to get you going. Let’s make sure you have everything you’ll need to tackle more challenging problems by watching the lesson below.

You’ll continue to explore all the key techniques, including:

• Addition
• Subtraction
• Multiplication
• Division
• Simplifying
• Comparing

Let’s get to it!

Video Tutorial — Full Lesson w/ Detailed Examples

1 hr 26 min

• Introduction to Video
• 00:00:38 – How do you convert?

• 00:03:50 – Write each number as a fraction in simplest terms (Examples #1-3)
• 00:09:48 – Record each problem as a fraction in lowest terms (Examples #4-6)
• 00:17:06 – How do you convert a repeating decimal into a fraction? (Example #7)
• 00:24:52 – Change the given statement into a fraction (Example #8-11)
• 00:40:00 – Convert the numbers into fractions (Examples #12-15)
• 00:59:46 – Perform the indicated operation by using the 3 step process (Examples #16-19)
• 01:17:02 – Write the correct comparison symbol by changing all problems (Examples #20-22)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions