Did you want to know the trick for comparing fractions?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Equivalent fractions!
Now equivalent fractions may have different numerators and denominators, but they represent the same value or proportion of the whole.
Let’s quickly remind ourselves of how we create equivalent fractions and simplify them using the two examples below.
Notice how four-fifths is equivalent to eight-tenths and twenty-five thirtieths is equivalent to five-sixth.
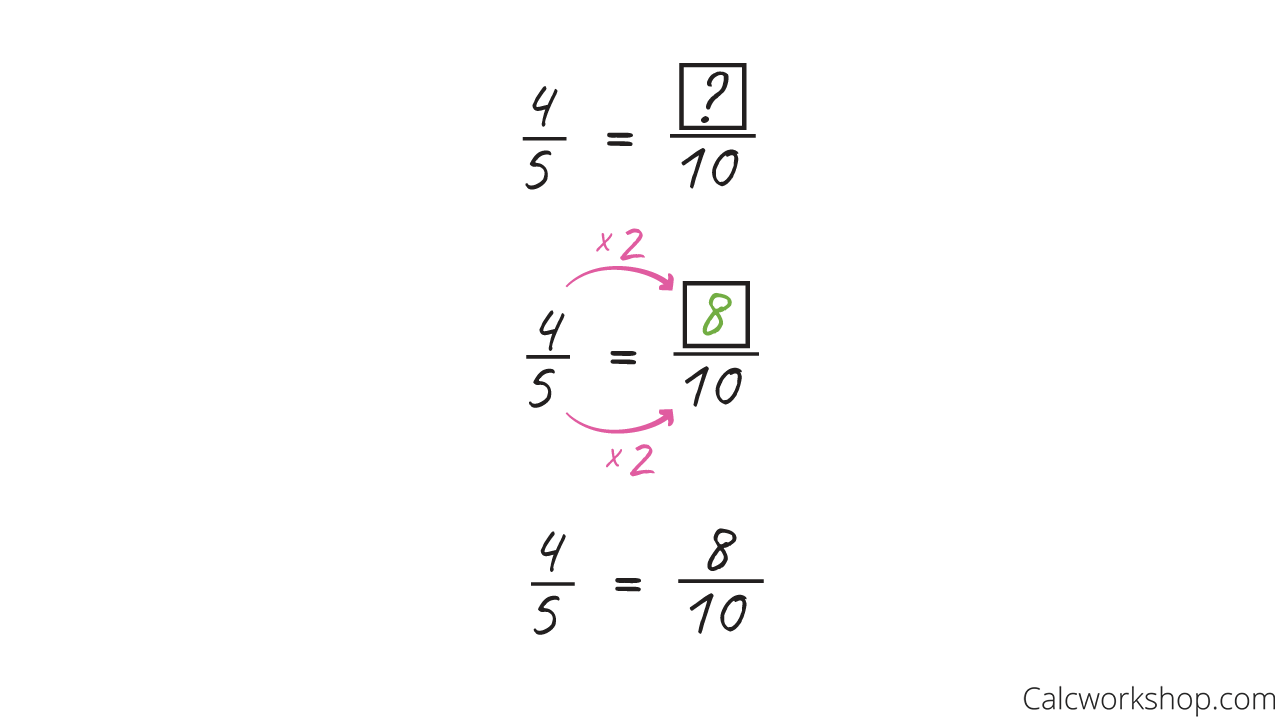
Multiply to Find Equivalent Fractions
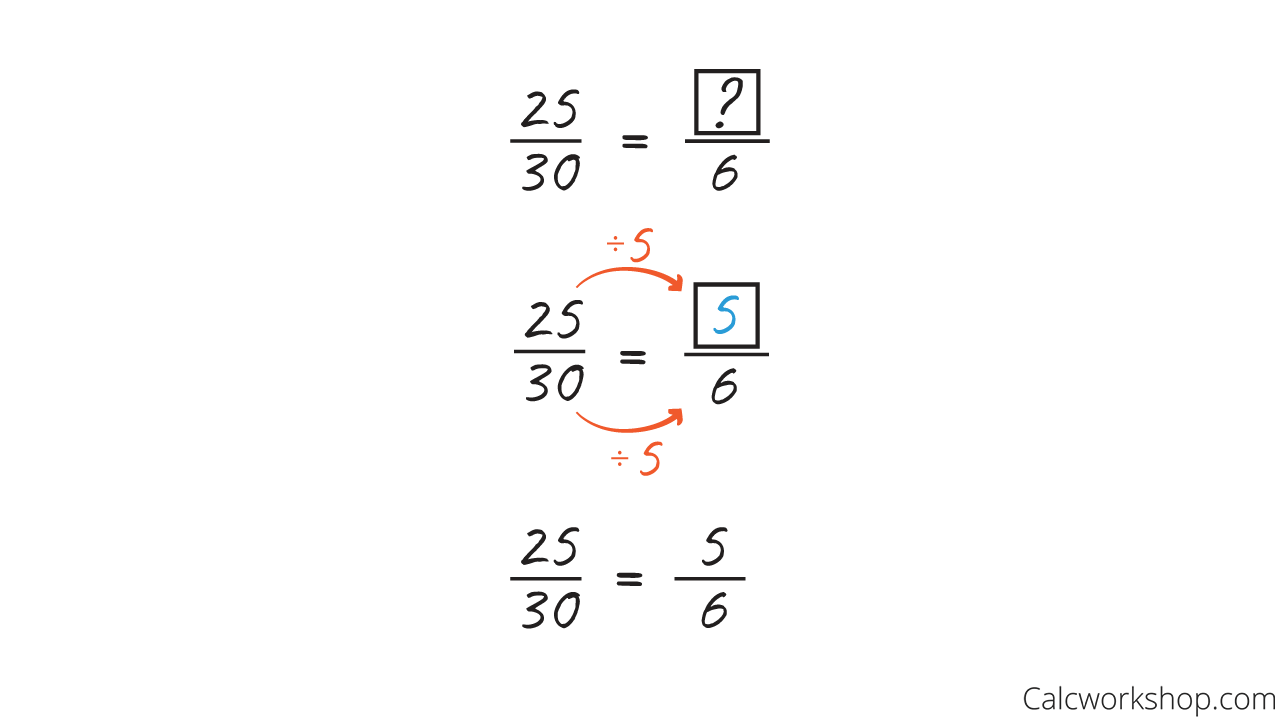
Divide to Find an Equivalent Fraction
But how does knowing how to create equivalent fractions help us compare fractions?
Well, to compare fractions, we have to ensure that we have common denominators. In other words, we can only compare fractions if the denominators are the same.
And the way we get common denominators is by creating fractions that have the same part to whole, as noted by Monterey Institute.
Finding Common Denominators
How do we determine the common denominators?
By using the Least Common Denominator (LCD)!
What’s cool is that the LCD uses the same process for finding the least common multiple (LCM), but only for the numbers in the denominator. This means we already know what to do.
Solved Example
For instance, let’s find common denominators for:
- 1/4
- 2/5
- First, we find the LCM of the denominators 5 and 4 by either listing multiples or using prime factorization.
- Then we create equivalent fractions for each using our new LCM.
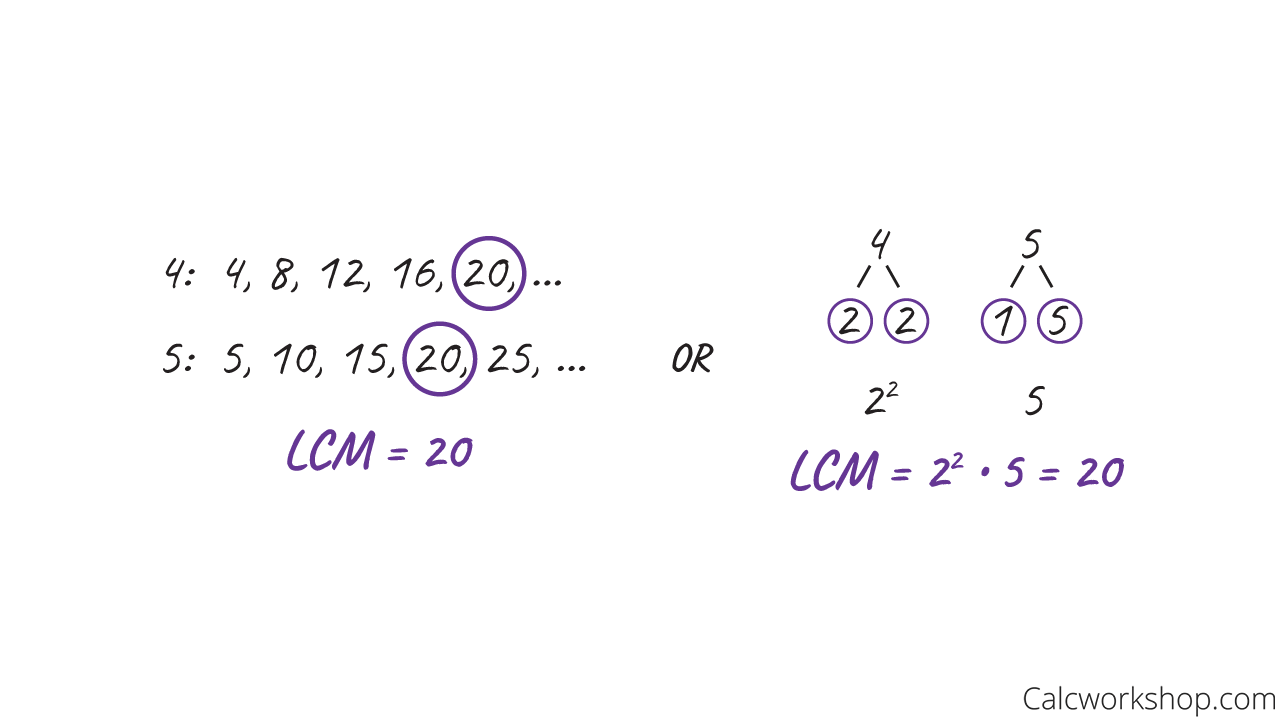
How To Find LCM Using Prime Factorization
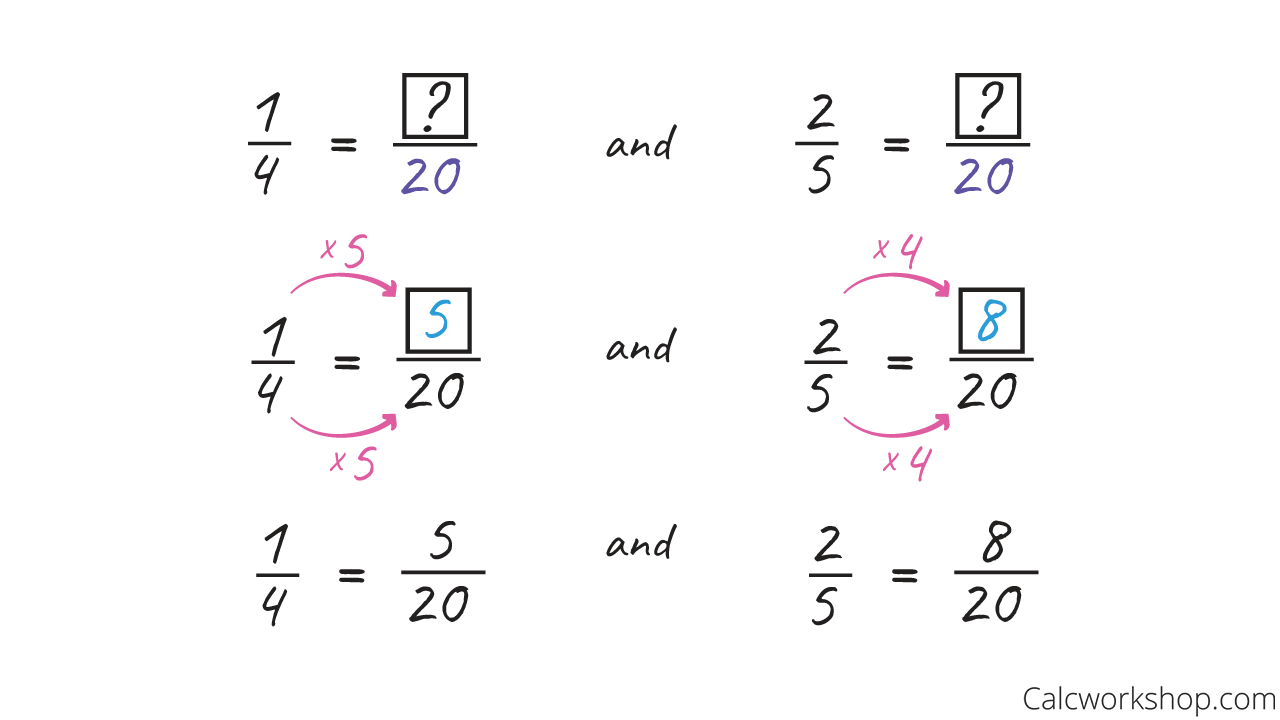
Equivalent Fractions with LCD
How To Compare Fractions
And now that we’ve found common denominators, we are ready to do a comparison of the fractions!
Because our denominators are the same, all we have to do is analyze our numerators to determine <, > or =.
Worked Example
So, let’s compare our two fractions of:
- 1/4
- 2/5
Thankfully, we already transformed these two fractions into equivalent fractions of 5/20 and 8/20 after finding common denominators, so all we have to do now is study their numerators.
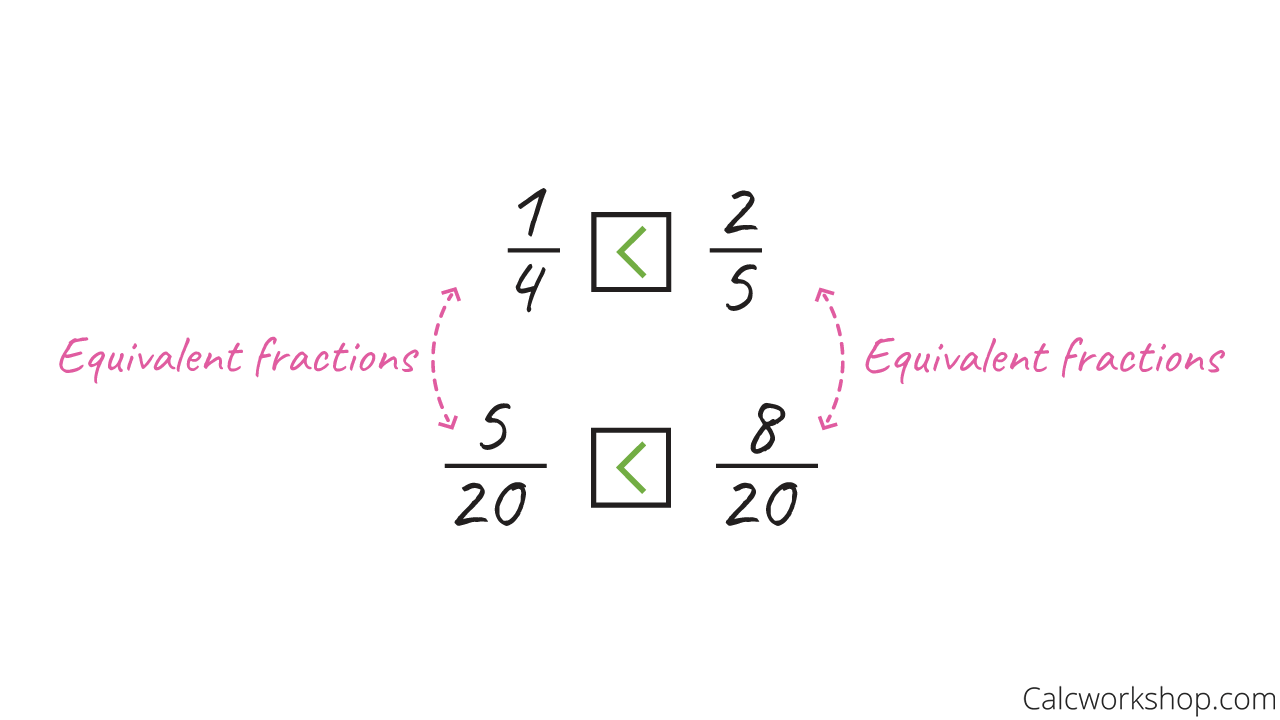
Compare Equivalent Fractions
That’s all there is to comparing fractions:
- Write each fraction with common denominators.
- Then compare their numerators.
Mixed Number vs. Improper Fraction
But what if we are working with an improper fraction with a mixed number?
You first want to change the mixed number into an improper fraction by multiplying the denominator by the whole number and adding the numerator, and then follow the steps listed above.
Detailed Example
For example, let’s work on the following problem:
- 14/3
- 5—1/2
First, we write the mixed number of 5 and 1/2 as an improper fraction of 11/2 using the technique we learned in our improper fraction mixed number video.

Compare Mixed Numbers and Improper Fractions
Next, we find the LCD by first finding the LCM of our denominators in order to create common denominators.
Because the LCM of 3 and 2 is 6, our least common denominator is 6.
So, now it’s time to create equivalent fractions.
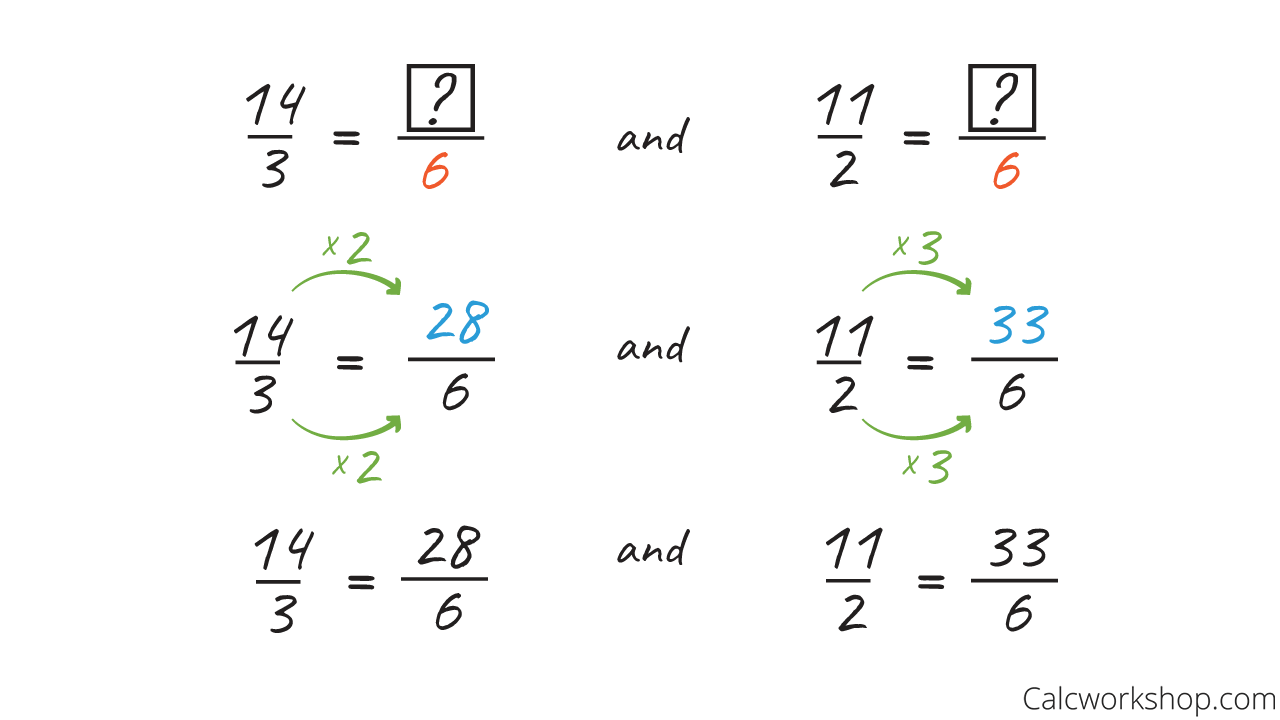
Comparing Improper Fractions
And since 28 is less than 33, then 28/6 is less than 33/6, which means 14/3 is less than 5 and 1/2.
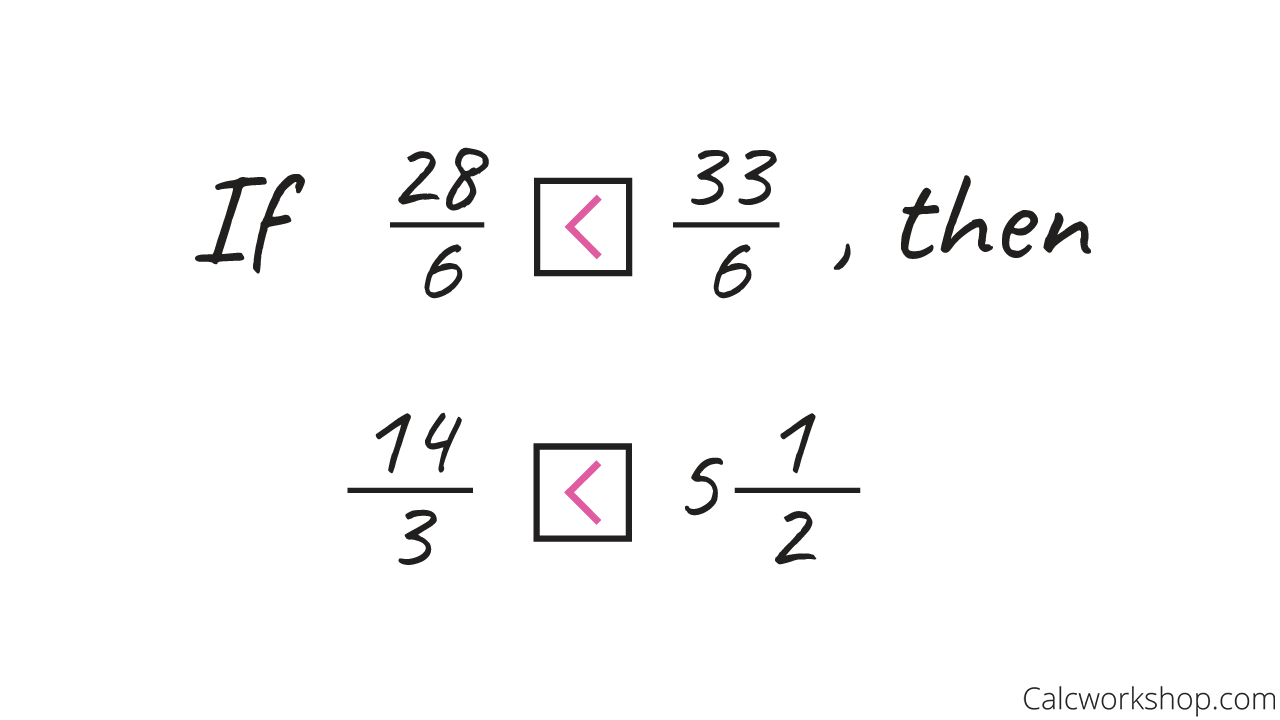
Improper Fractions — Comparison
Cool!
How To Compare More Than 2 Fractions
Okay, so what do we do when we want to equate more than two fractions?
Whenever this happens, you are asked to list each fraction in order from least to greatest (ascending) or greatest to least (descending), just like we did in our decimals lesson.
Key Example
Once again, the key to listing fractions in order is to first get common denominators!

List of Fractions in Order
Worksheet (PDF) — Hands on Practice
Put that pencil to paper in these easy to follow worksheets — expand your knowledge!
Comparing Fractions — Practice Problems
Comparing Fractions — Step-by-Step Solutions
Summary
In the video below, we will look at additional examples of how to compare fractions by finding the least common denominator and how to order fractions from least to greatest, as well as looking at some helpful tricks and tips along the way.
Let’s do it!
Video Tutorial — Full Lesson w/ Detailed Examples
1 hr 12 min
- Introduction to Video
- 00:00:39 – Least Common Denominator and Equivalent Fractions (Examples #1-3)
- 00:09:20 – Compare fractions by finding the LCD (Examples #4-7)
- 00:25:59 – Tips and Tricks for mixed numbers and improper fractions
- 00:28:47 – Comparison of improper fractions and mixed numbers (Examples #8-10)
- 00:38:22 – Compare each fraction using <,>,or = (Examples #11-14)
- 00:54:43 – Order the fractions from least to greatest (Examples #15-17)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.