Sometimes the first step in solving a differential equation is to make a substitution.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Why?
Because the current equation doesn’t seem to fit any of the known classifications or procedures we know of for solving. Therefore, a substitution or transformation is required.
But first, we need to talk about homogeneous first order differential equations and its alternative definition.
Homogeneous First Order Differential Equations and Alternative Definition
We learned earlier that a linear first-order differential equation is \(a_{1}(x) y^{\prime}+a_{0}(x) y=0\), but there is an alternative definition that we will be using for solutions by substitutions.
Let’s look at it now.
A first order DE in the form \(M(x, y) d x+N(x, y) d y=0\) is said to be homogeneous if both coefficient functions \(\mathrm{M}\) and \(\mathrm{N}\) are homogeneous functions of the same degree such that
\begin{align*}
M(t x, t y)=t^{n} M(x, y) \text { and } \quad N(t x, t y)=t^{n} N(x, y)
\end{align*}
But why is this important?
Importance of Homogeneous Functions and Substitution Choices
Because if \(\mathrm{M}\) and \(\mathrm{N}\) are homogeneous functions of degree \(\mathrm{n}\), then we can make either of the following substitutions \(y=u x\) or \(x=v y\), where \(\mathrm{u}\) and \(\mathrm{v}\) are new dependent variables; thus, reducing the equation to a separable first-order DE.
But how do we know which substitution to use?
Easy! We just look for which function, \(\mathrm{M}\) or \(\mathrm{N}\), is easiest or less complicated.
Steps for Solving by Substitutions
Let’s outline the steps for solving by substitutions and then look at an example to make sense of things.
- 1. Determine which function appears less complicated. If \(M(x, y)\) is “easiest” then substitute \(y=u x\). If \(N(x, y)\) is less complicated, then substitute \(x=v y\).
It is important to note that this type of substitution, or change of variables, is very similar to u-substitution from calculus, in the sense that when you change \(\mathrm{y}\) or \(\mathrm{x}\) you will also need to change \(\mathrm{dx}\) or \(\mathrm{dy}\) accordingly.
- 2. Simplify our equation and separate our equation using the method of separable equations.
- 3. Resubstitute our variables to arrive at our general solution. Alright, let’s try it!
Example: Solving Differential Equation with Substitution
Using an appropriate substitution, solve the differential equation
\begin{equation}
(x-y) d x+x d y=0
\end{equation}
First, we need to select the least complicated function, either \(\mathrm{M}\) or \(\mathrm{N}\).
\begin{equation}
\underbrace{(x-y)}_M d x+\underbrace{(x)}_N d y=0
\end{equation}
Because \(\mathrm{N}\) is less complicated, we will substitute \(x=v y\), which also means we will need to find \(\mathrm{dx}\) as well. In other words, if \(x=v y\), then using implicit differentiation and the product rule we let \(d x=v d y+y d v\)
Now we substitute \(x=v y\) and \(d x=v d y+y d v\) into our differential equation and simplify.
\begin{equation}
(x-y) d x+x d y=0
\end{equation}
\begin{equation}
(v y-y)(v d y+y d v)+(v y) d y=0
\end{equation}
Simplifying the Example Equation with Separation of Variables
Next, we will use the method of separation of variables by getting all the y’s on one side and all the v’s on the other.
1. Start by expanding the expression on the left-hand side of the equation:
Comment: Multiplying the terms and combining them with the second term.
\[
(v y-y)(v d y+y d v)+(v y) d y=0
\]
\[
v^{2} y d y+v y^{2} d v-v y d y-y^{2} d v+v y d y=0
\]
2. Simplify by combining like terms:
\[
v^{2} y d y-v y d y+v y d y+v y^{2} d v-y^{2} d v=0
\]
\[
v^{2} y d y+v y^{2} d v-y^{2} d v=0
\]
3. Factor out common terms:
Comment: Factoring ydy from the “dy” term and y²dv from the “dv” terms.
\[
y d y\left(v^{2}\right)+y^{2} d v(v-1)=0
\]
4. Subtract the “dv” term to the other side of the equal sign:
\[
y d y\left(v^{2}\right)=-y^{2} d v(v-1)
\]
5. Use Separate of Variables so that all the “ys” are on one side and all the “vs” are on the other:
\[
\frac{y d y}{-y^{2}}=\frac{(v-1) d v}{\left(v^{2}\right)}
\]
6. Simplify the left-hand side and the right-hand side of the equation:
\[
\frac{y d y}{-y^2}=\frac{v-1}{v^2} d v
\]
\[
-\frac{y}{y^2} d y=\left(\frac{v}{v^2}-\frac{1}{v^2}\right) d v
\]
\[
-\frac{1}{y} d y=\left(\frac{1}{v}-\frac{1}{v^2}\right) d v
\]
Integration and Resubstitution for the Example Equation
Now it is time to integrate both sides and solve for \(\mathrm{y}\)
\[
\int-\frac{1}{y} d y=\int\left(\frac{1}{v}-\frac{1}{v^2}\right) d v
\]
\[
-\ln |y|=\ln |v|+\frac{1}{v}+C
\]
Lastly, we will resubstitute \(x=v y\), which is the same as \(v=\frac{x}{y}\) into our equation to find our general solution.
1. Start with the given equation:
Comment: The equation relating the natural logarithm of y to x and a constant C.
\[
-\ln |y|=\ln \left|\frac{x}{y}\right|+\frac{1}{(x / y)}+C
\]
2. Simplify the equation
\[
-\ln |y|=\ln \left|\frac{x}{y}\right|+\frac{y}{x}+C
\]
3. Break up the logarithm on the right-hand side:
Comment: Using the property of logarithms ln(a/b) = ln(a) – ln(b).
\[
-\ln |y|=\ln |x|-\ln |y|-\frac{y}{x}+C
\]
4. Add ln|y| to both sides of the equation. Notice the ln|y| terms cancel out.
\[
0=\ln |x|-\frac{y}{x}+C
\]
5. Multiply both sides by x to eliminate any fractions:
\[
0=x \ln |x|-y+C x
\]
6. Solve for y:
\[
y=x \ln |x|+C x
\]
Conclusion
Granted, this process can be tedious at times and forces us to draw upon our knowledge of differentiation, integration, and logarithms, but it isn’t hard to grasp and is an extremely useful method for solving first order differential equations.
In fact, Paul’s Online Notes encourages us to never forget this powerful tool of substitution as it is a great way to solve a differential equation that doesn’t seem to fit the mold.
Next Steps
So, together, we will:
- Look at the steps for solving Homogeneous First Order ODEs,
- Make a substitution that will transform our given differential equation into a linear differential equation with an integrating factor, and
- Walk through several examples in detail.
Let’s get after it.
Video Tutorial w/ Full Lesson & Detailed Examples
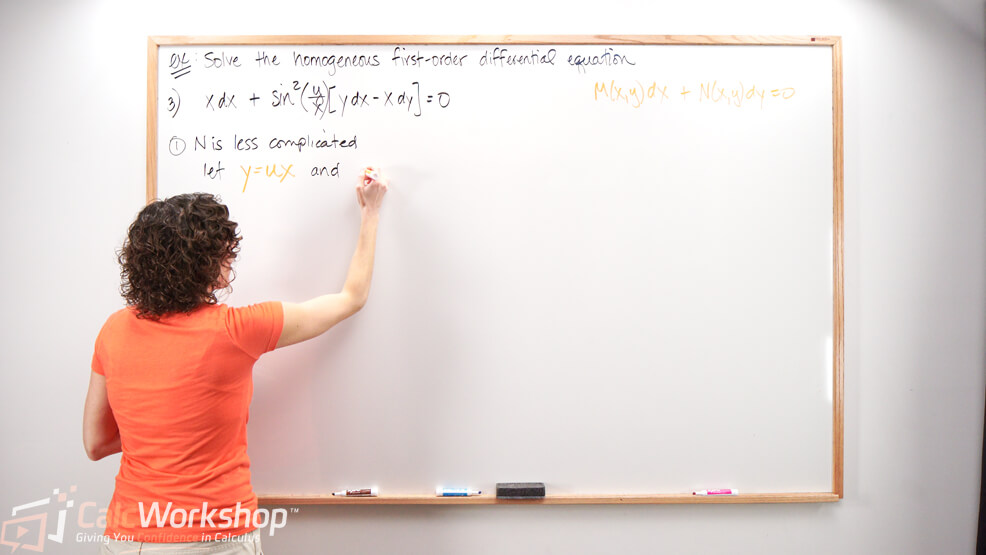
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.