Did you know that the transformation of random variables is the same process as for data sets?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
Just like we saw in our previous unit of exploring data where we learned how transforming data affects:
- Shape
- Center
- Spread of the Distribution
We will see that similar techniques can be applied to transform the mean and variance of discrete probability distributions.
Let’s get started!
Review:
- Adding the same number (positive or negative) to an observation will shift the center and location of a distribution, but it will not change the distribution’s shape or spread. This means that the mean, median, quartiles, and percentiles will all shift the same amount as the added value, but the range, IQR, and standard deviation will stay the same.
- Multiplying by a fixed number will shift the center, location, and spread of a distribution, but it will not change the shape of the distribution. In other words, the mean, median, quartiles, range, IQR, and standard deviation will all shift, but the overall shape will stay the same.
These effects are the same for a random variable and can be applied to expectancy and standard error.
Let’s look at the three properties for transforming and combining discrete random variables.
- If X and Y are random variables, and a and b are fixed numbers, and Y = a +bX, then the probability distribution of Y has the same shape as the probability distribution of X and:
- If T = X + Y is the sum of two random variables and T = X – Y is the difference of two random variables. The mean of the sum or difference is the sum or difference of their means as long as X and Y are independent random variables.
- If T = X + Y or T = X – Y, then T’s variance is the sum of their variances.
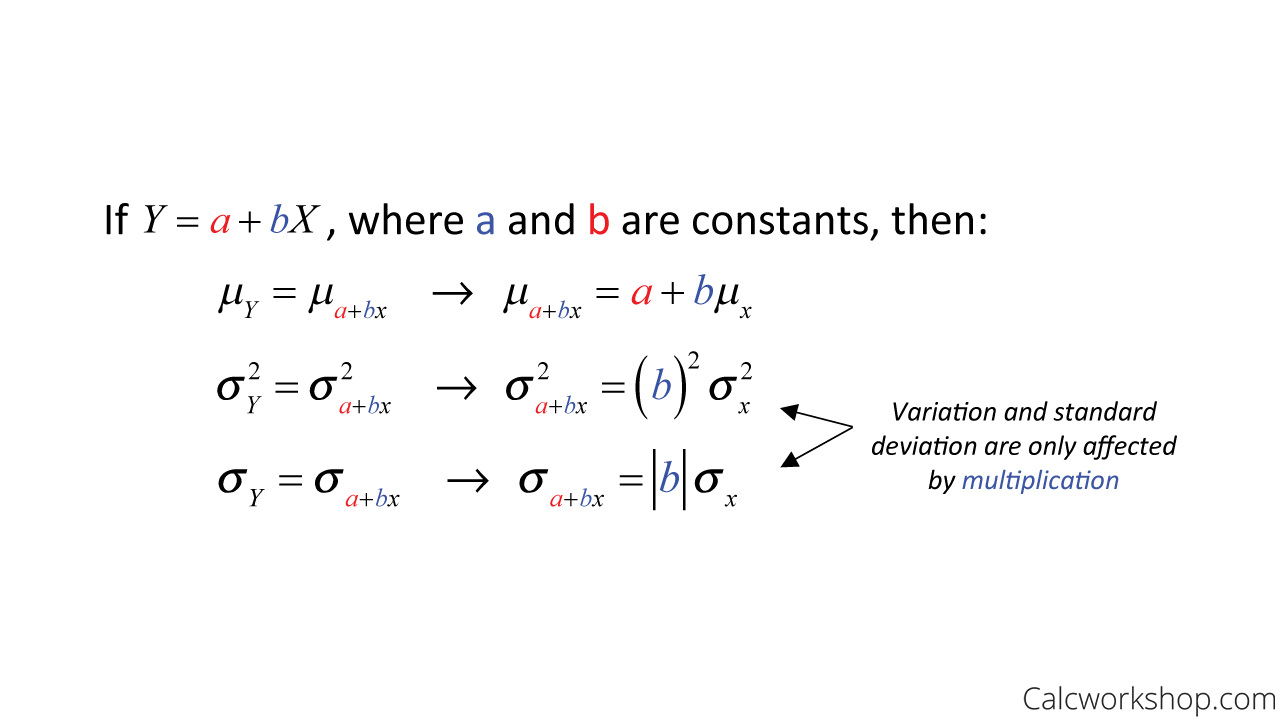
Mean And Variance Formulas For Linear Combinations
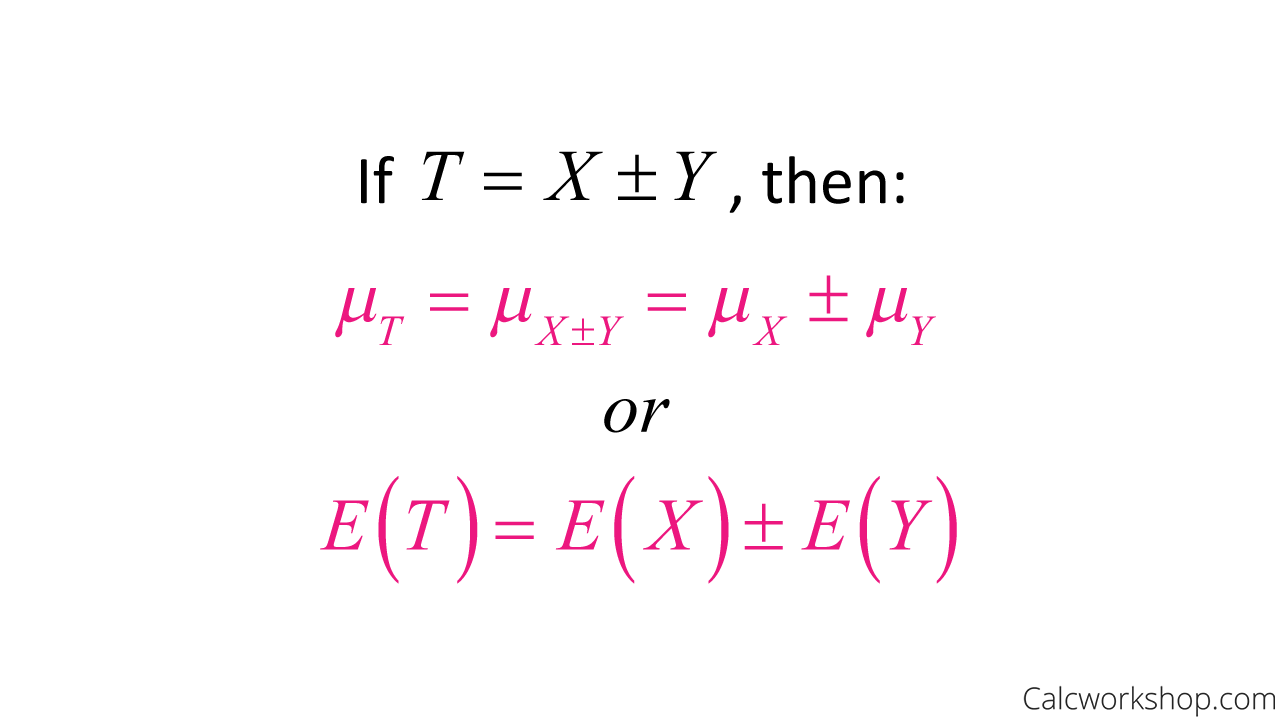
Mean Of Two Random Variables
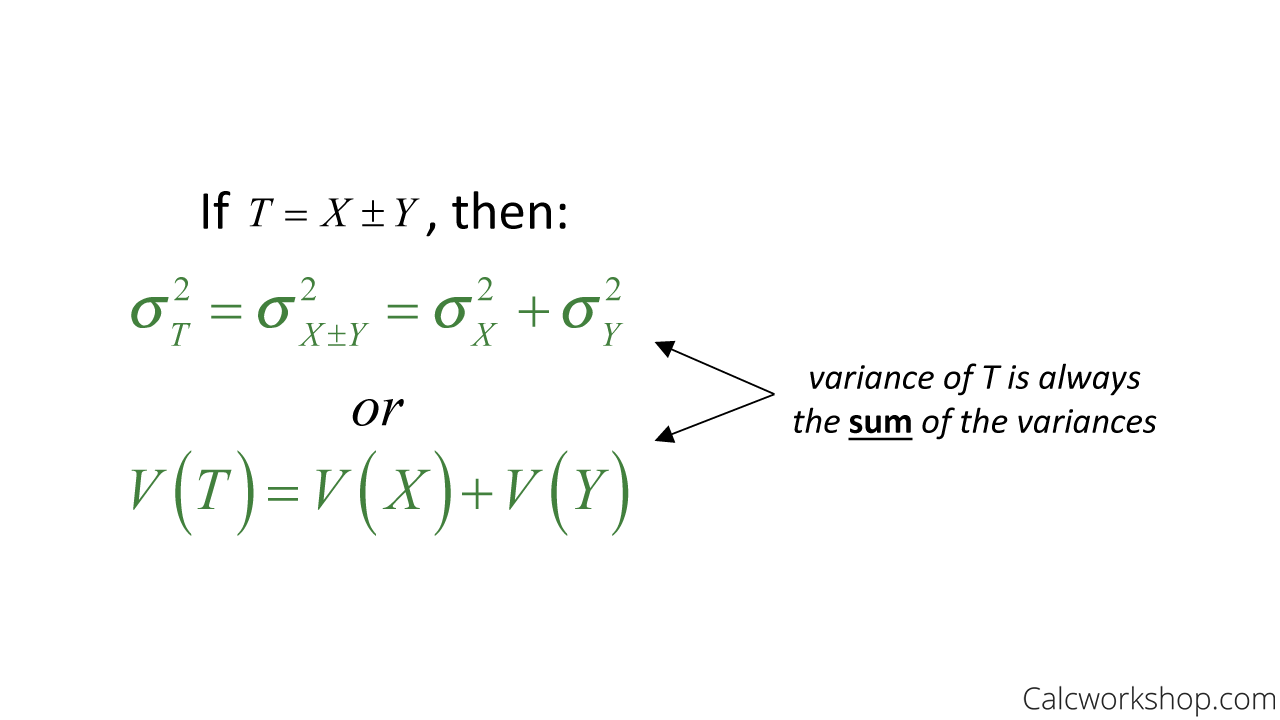
Variance Of Two Random Variables
Example
This is made clear with examples, so let’s look at these properties in action!
Suppose X and Y are two independent, discrete random variables with E(X)=10, V(X)=5, E(Y)=20, and V(Y)=3. Calculate the following:

Two Variable Problem For The Mean And Variance
All we have to do is follow our formulas, as seen below:

Solution For The Mean And Variance Of A Two Variable Problem
That’s it!
Throughout this video lesson, we will walk through numerous examples in detail for finding the mean and variance of a transformed random variable and how to combine random variables for discrete probability distributions.
Transformation of Random Variables – Lesson & Examples (Video)
49 min
- Introduction to Video: Transforming and Combining Discrete Random Variable
- 00:00:39 – Overview of how to transform a random variable and combine two random variables to find mean and variance
- Exclusive Content for Members Only
- 00:06:03 – Find the new mean and variance (Example #1)
- 00:10:50 – Find the new mean and variance given two discrete random variables (Example #2)
- 00:23:20 – Find the mean and variance of the probability distribution (Example #3)
- 00:36:11 – Find the mean and standard deviation of the probability distribution (Example #4a)
- 00:39:38 – Find the new mean and standard deviation after the transformation and graph the distribution (Example #4b)
- 00:46:12 – Find the mean and standard deviation of the linear transformation (Example #4c)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.