In a Poisson Distribution, we are interested in whether events occur randomly in time or space.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
For example:
- The number of calls per hour
- The number of prairie dogs in a field
- The number of births in a year
- The number of viral cases in a city
- Etc.
Are all examples of situations in which we observe the numerical values of a random variable within a set time interval (minute, hour, day, year, etc.) or specified region (length, area, volume).
Formulas
The Poisson Distribution, named after French mathematician Siméon Denis Poisson, is a discrete probability distribution with the following conditions and formulas:
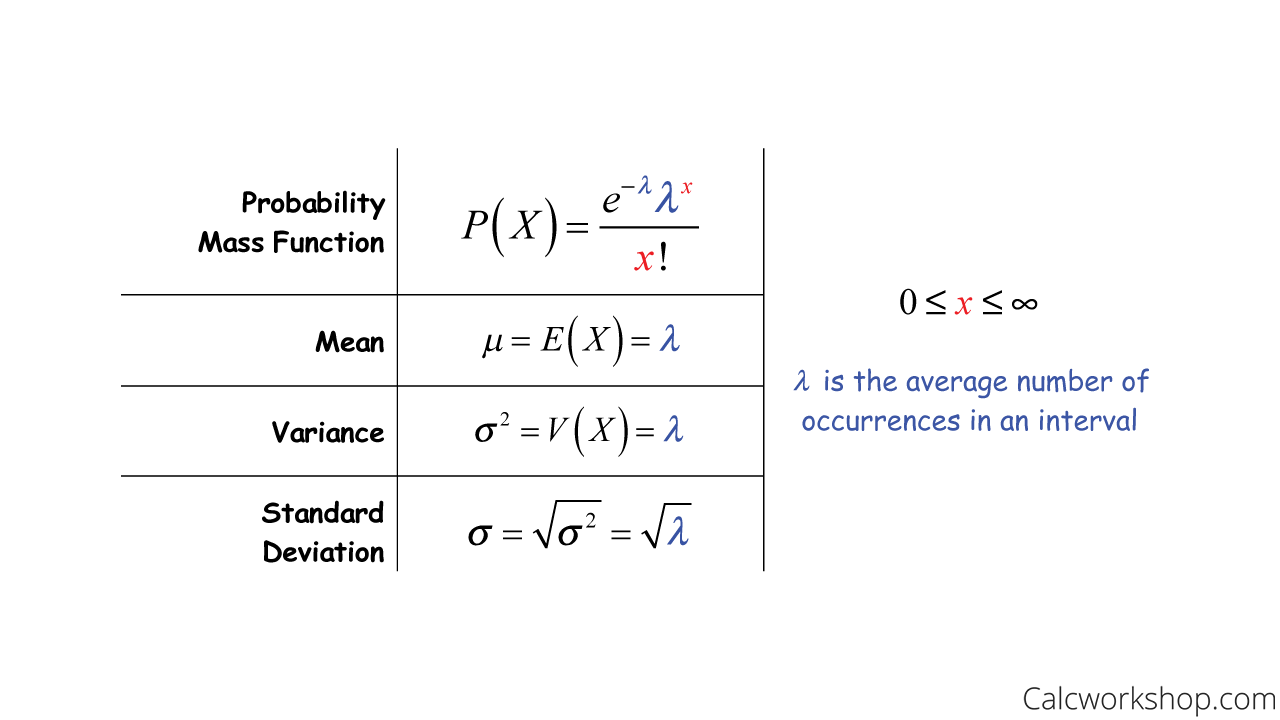
Poisson Distribution (PMF, Mean, Variance, And Standard Deviation)
The average number of outcomes or successes occurring in one time interval or specified region is independent and lacks memory, similar to the geometric and exponential distributions. This fact is confirmed in a post by Towards Data Science as well.
The probability of one count in a subinterval is the same for all subintervals and proportional to the length of the subinterval.
The probability that more than one outcome will occur in a subinterval is negligible or almost zero.
And the Poisson distribution becomes more symmetric, or bell-shaped, as the mean grows large.
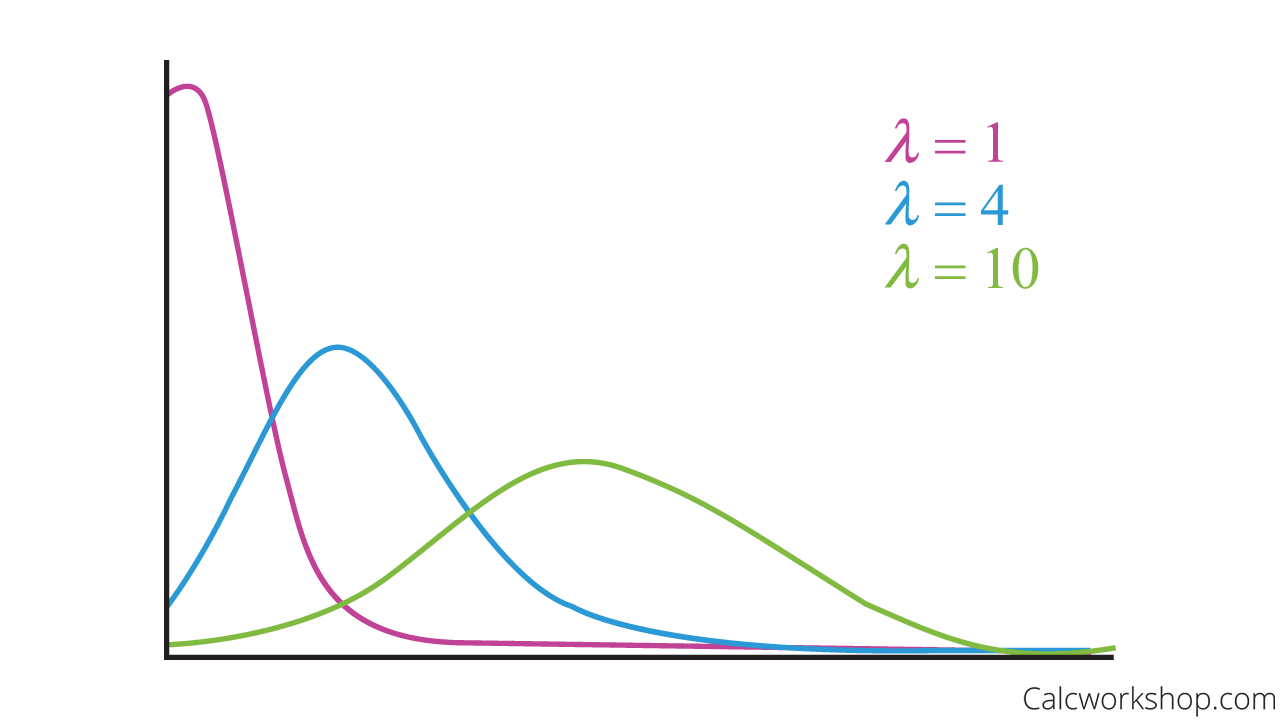
Poisson Distribution Curve
It is important to note that the Poisson differs from the previous discrete distributions in the sense that there isn’t a limit to the number of possible outcomes. The Binomial Distribution along with the Geometric, Hypergeometric, and Negative Binomial Distributions are all binary in nature, meaning they are used when each observation represents two possible outcomes (success or failure). Still, the Poisson distribution is used for events that could occur a large number of times.
But even so, it can still be challenging to know when to use the Poisson Distribution and when to choose another discrete distribution for a given problem.
So, let me give you a big hint…
…always use the Poisson Distribution when you’re given the average probability of an event happening per unit of time or space, and you want to find the likelihood of a certain number of events happening in a period of time or space.
Ah, so the key is the “average”!
Worked Example
Let’s look at an example.
Suppose a local retail store can expect three customers to enter the establishment every 10 minutes, on average. What is the probability that four or fewer customers will enter the store in twenty minutes?
Notice that we were given an average amount in a specified time interval, so we know we’re going to be using the Poisson Distribution.
And, we are told that, on average, three customers enter the store every ten minutes, so we would expect to see six customers in 20 minute period. Our job is to determine the likelihood that four or fewer customers will enter the store in the same 20 minute period. In other words, what is the probability that 0, 1, 2, 3, or 4 customers enter the store in 20 minutes?
So, knowing that the specified time interval is 20, the average value is six customers, so we use our Poisson Distribution formula, as shown below.
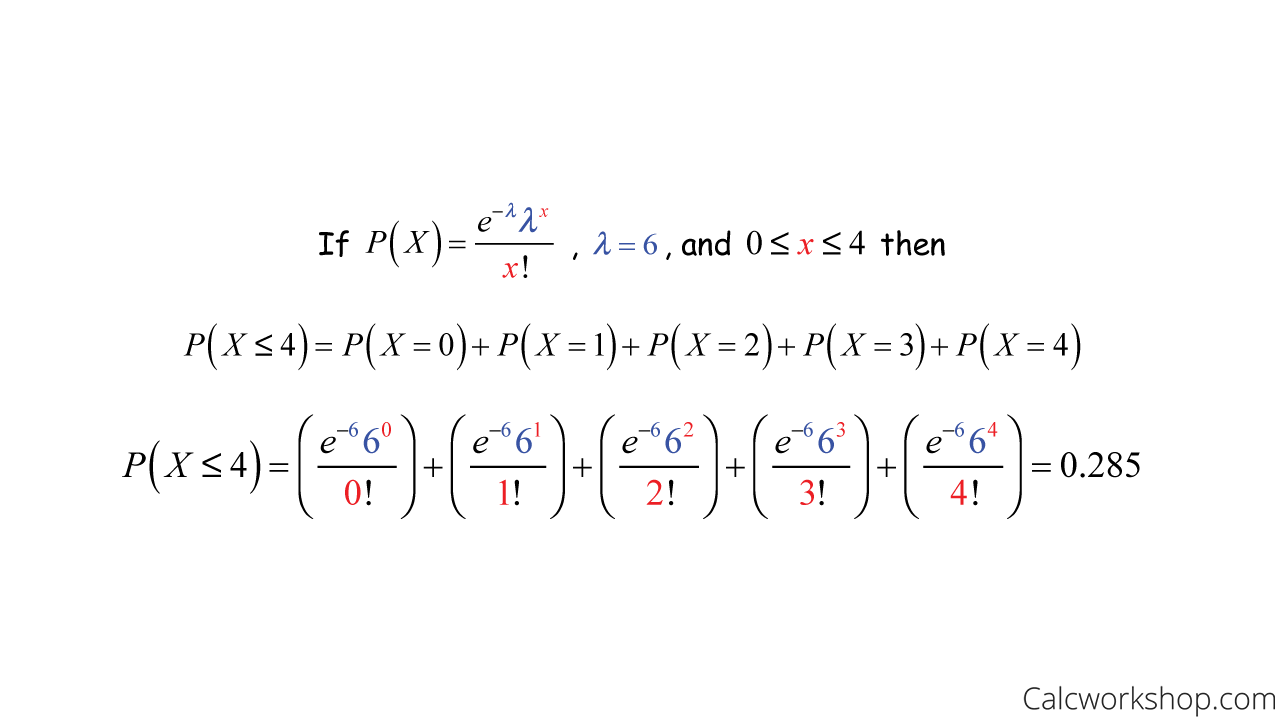
Poisson Probability CDF Example
Therefore, the probability that four or fewer customers enter the store in twenty minutes is 0.285
Not so bad!
Throughout this lesson will walk you through detailed examples of how to recognize the Poisson distribution and how to use the formulas for probability, expectancy, and variance without getting lost or confused.
Let’s do it!
Poisson Distribution – Lesson & Examples (Video)
52 min
- Introduction to Video: Poisson Distribution
- 00:00:48 – Overview of the Poisson Distribution and it’s properties
- Exclusive Content for Members Only
- 00:09:43 – Given a Poisson distribution find the probability, expectation and standard deviation (Examples #1-2)
- 00:22:17 – Find the probability and cumulative probability given a Poisson Distribution (Examples #3-4)
- 00:34:35 – Find the expected cost using definition of expectation for a poisson distribution (Example #5)
- 00:42:33 – Verify the expected value of a Poisson distribution using Taylor series (Example #6)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.