Have you ever practiced something until you mastered it?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Well, this is the idea behind the Geometric Distribution – experimenting until success is obtained!
A geometric random variable has conditions, just like the binomial random variable.
And the easiest way for us to remember these conditions is to recognize the BINS!

Geometric Distribution Mnemonic
Binomial Vs Geometric Distribution
Notice that the only difference between the binomial random variable and the geometric random variable is the number of trials: binomial has a fixed number of trials, set in advance, whereas the geometric random variable will conduct as many trials as necessary until the first success as noted by Brilliant.
Worked Example
So, let’s see how we use these conditions to determine whether a given random variable has a geometric distribution.
For example, suppose we shuffle a standard deck of cards, and we turn over the top card. We put the card back in the deck and reshuffle. We repeat this process until we get a Jack. Is this a geometric distribution?
All we have to do is check the BINS!
B – binary – yes, either it’s a Jack or not a Jack
I – independent – yes, because we replace the card each time, the trials are independent.
N – number of trials until you get a success – yes, we are told to repeat until we get a Jack.
S – success (probability of success) the same – yes, the likelihood of getting a Jack is 4 out of 52 each time you turn over a card.
Therefore, this is an example of a geometric distribution.
Okay, so now that we know the conditions of a Geometric Random Variable, let’s look at its properties:
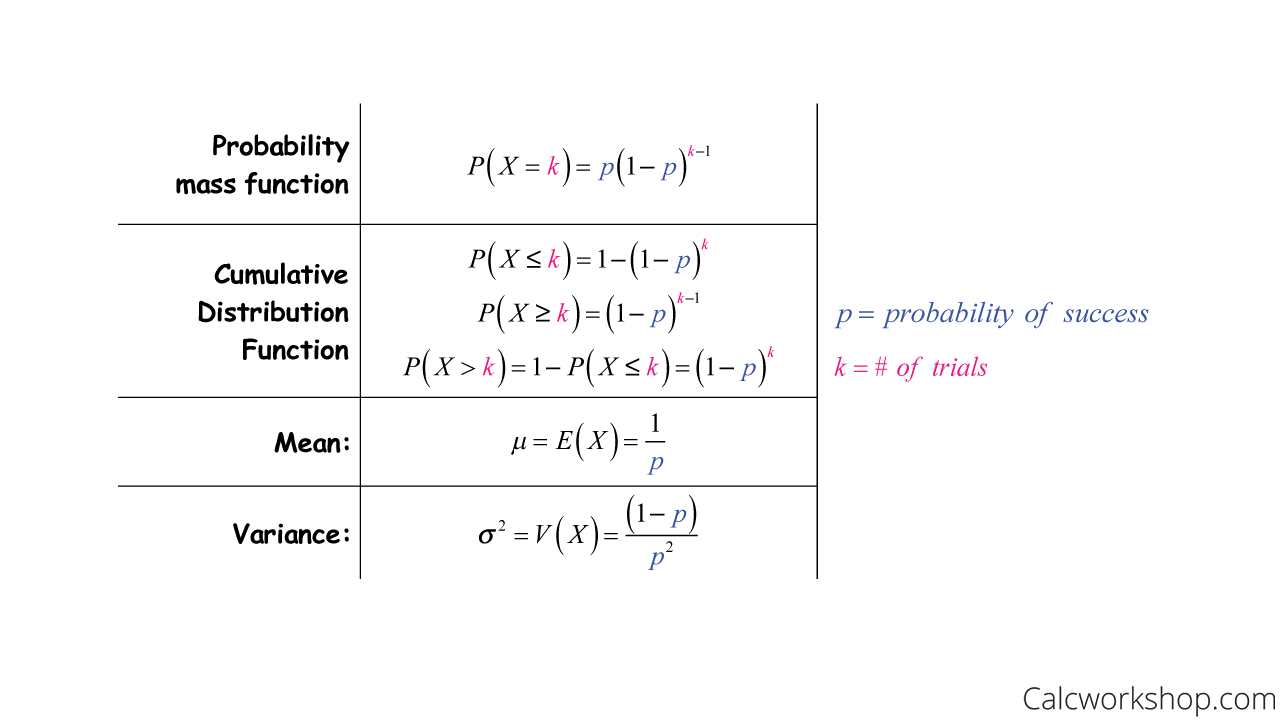
Mean And Variance Of Geometric Distribution (PMF & CDF)
Worked Example
Now, let’s investigate how to use the properties with an example.
Suppose Max owns a lightbulb manufacturing company and determines that 3 out of every 75 bulbs are defective. What is the probability that Max will find the first faulty lightbulb on the 6th one that he tested?
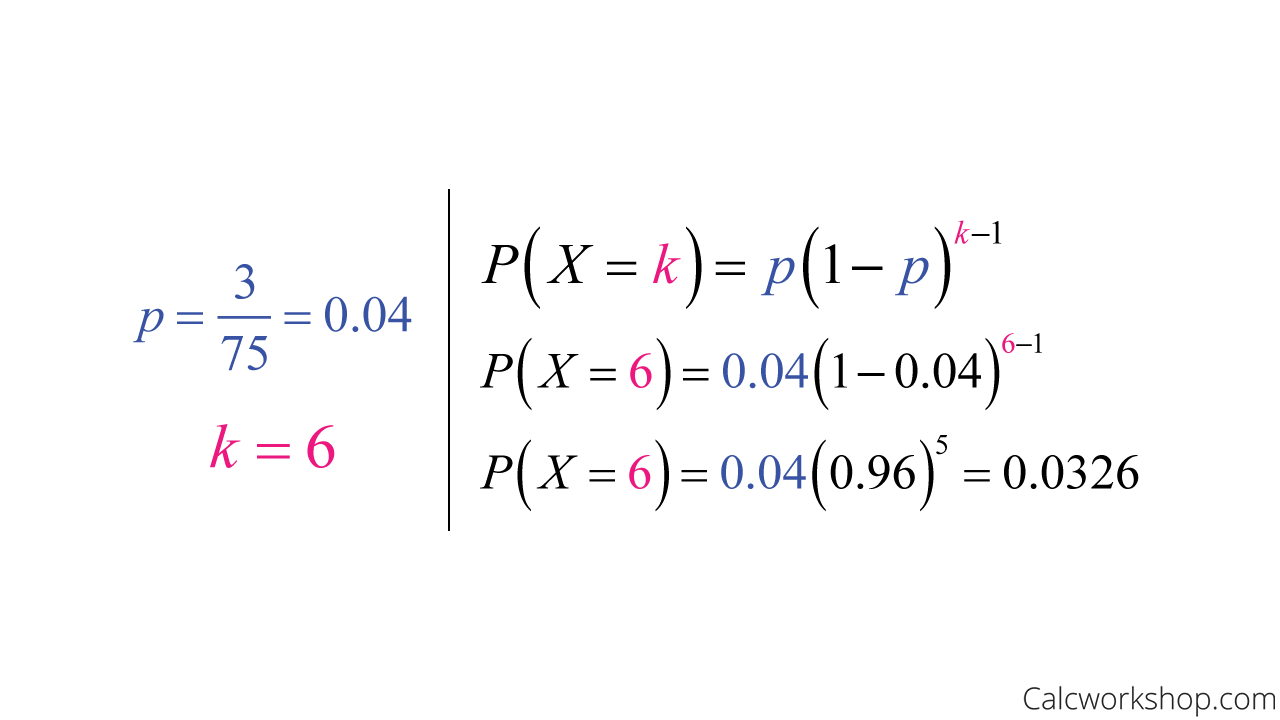
Geometric Probability Problem
This means that the likelihood of Max finding the first defective lightbulb on the 6th one he tests is 0.0326.
Now, what if Max wants to know the likelihood that it takes at least six trials until he finds the first defective lightbulb?
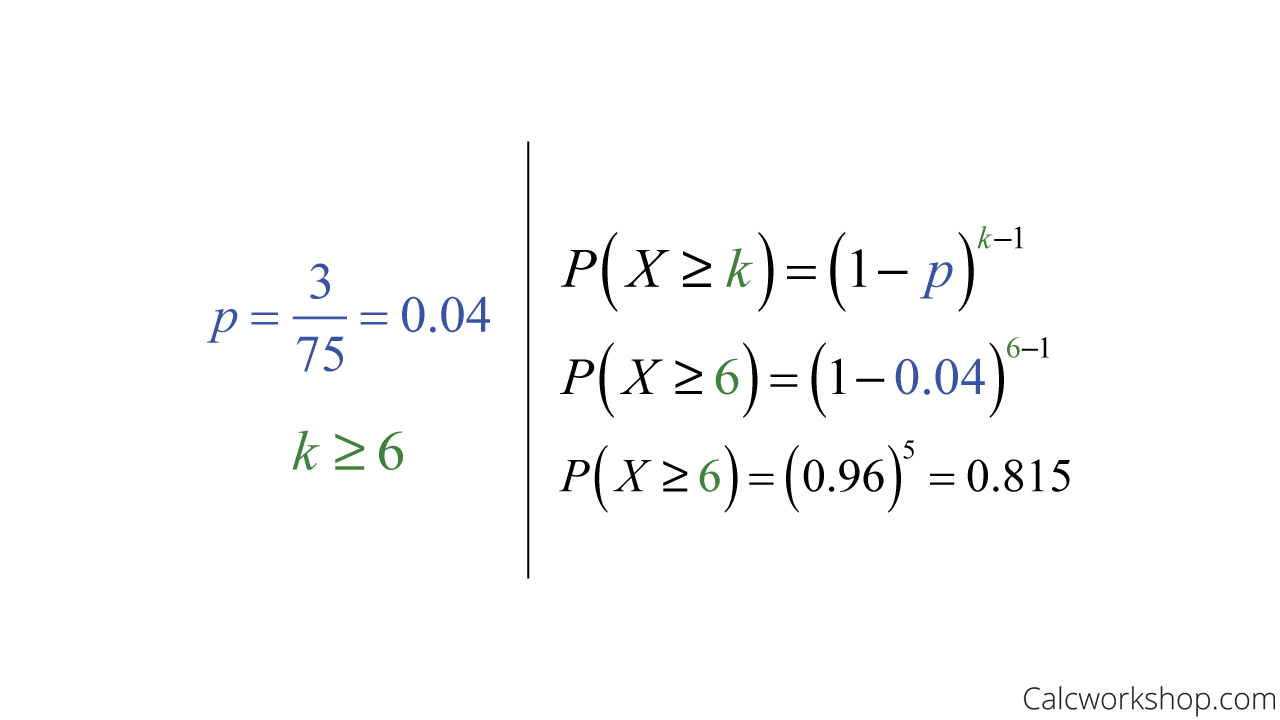
Example Of Geometric CDF
Using the formula for a cumulative distribution function of a geometric random variable, we determine that there is an 0.815 chance of Max needing at least six trials until he finds the first defective lightbulb.
And using this same example, let’s determine the number lightbulbs we would expect Max to inspect until he finds his first defective, as well as the standard deviation.
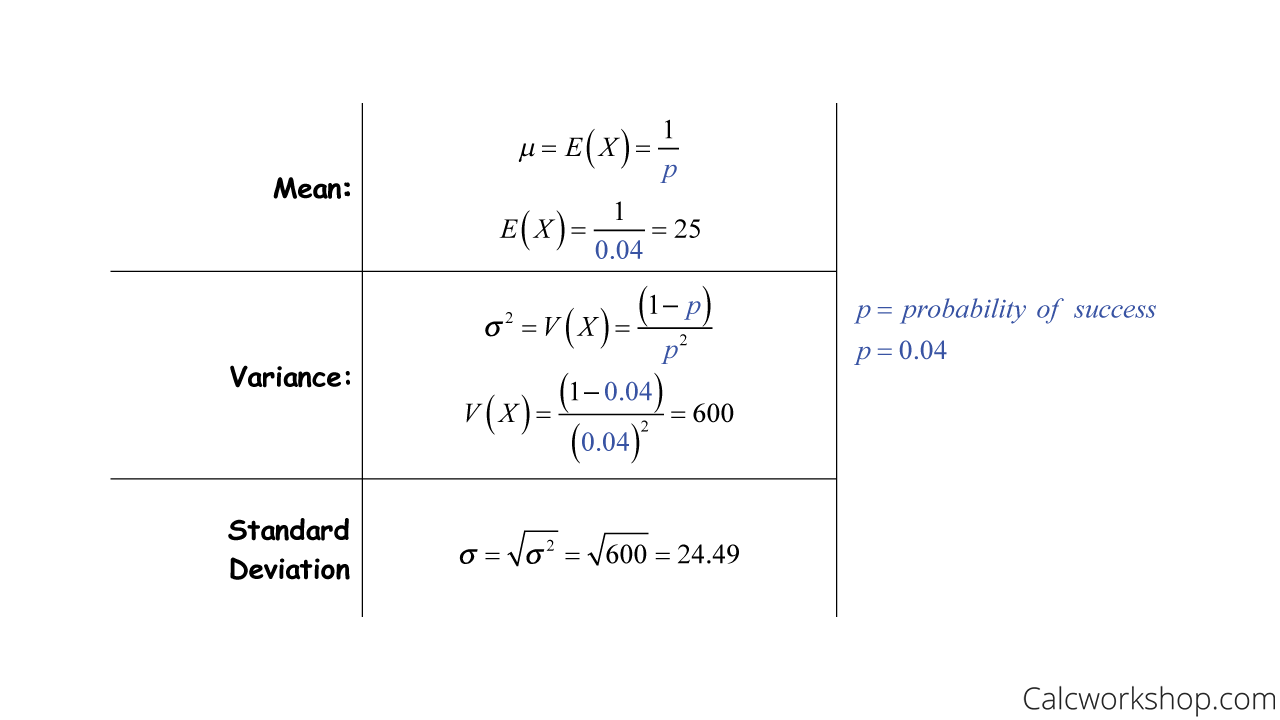
Geometric Distribution Example
This shows us that we would expect Max to inspect 25 lightbulbs before finding his first defective, with a standard error of 24.49.
What this example nicely shows is that sometimes we are more interested in the number of failures rather than the number of successes. Notice that Max was inspecting lightbulbs until he found his first defective (i.e., his first failure), and the geometric distribution was the perfect tool to help.
Throughout this video, we will utilize our conditions for geometric random variables and apply our properties to find
- Expectancy
- Variance
- Probabilities
By using both PMF and CDF formulas of geometric distributions.
Additionally, we will introduce the lack of memory property that applies to both the geometric and exponential distributions.
Geometric Distribution – Lesson & Examples (Video)
44 min
- Introduction to Video: Geometric Distribution
- 00:00:33 – Overview of Geometric Random Variable with Examples #1-3
- Exclusive Content for Members Only
- 00:16:29 – Find the probability, expected value and variance for the geometric distribution involving the success of starting a lawnmower(Example #4)
- 00:28:03 – Find the probability and expectation for the distribution of rolling two dice (Example #5)
- 00:34:26 – Find the probability, expected value, and variance for passing a placement test (Example #6)
- 00:41:30 – Overview of Lack of Memory principle for geometric distributions
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.