What is a discrete random variable?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question.
That’s exactly what we’re going to learn about in today’s statistics lesson.
Let’s get started!
Did you know that a random variable is a function that assigns a real number with each outcome in the sample space?
For example, imagine you toss a coin twice, so the sample space is {HH, HT, TH, TT}, where H represents heads, and T represents tails. And you want to determine the number of heads that come up. Well, we would count the number of heads (outcomes) in the sample space, as demonstrated.
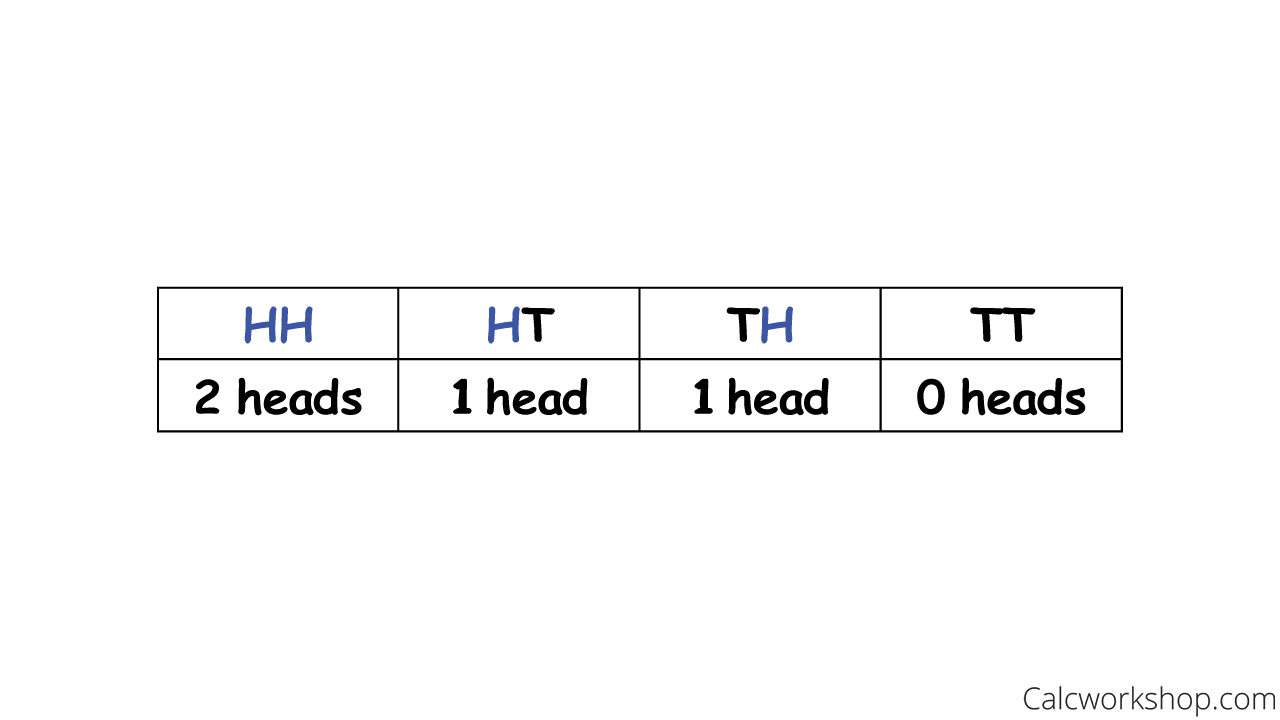
Sample Space Of Head And Tails
The number of heads that you count is called a random variable and is typically denoted as X or Y.
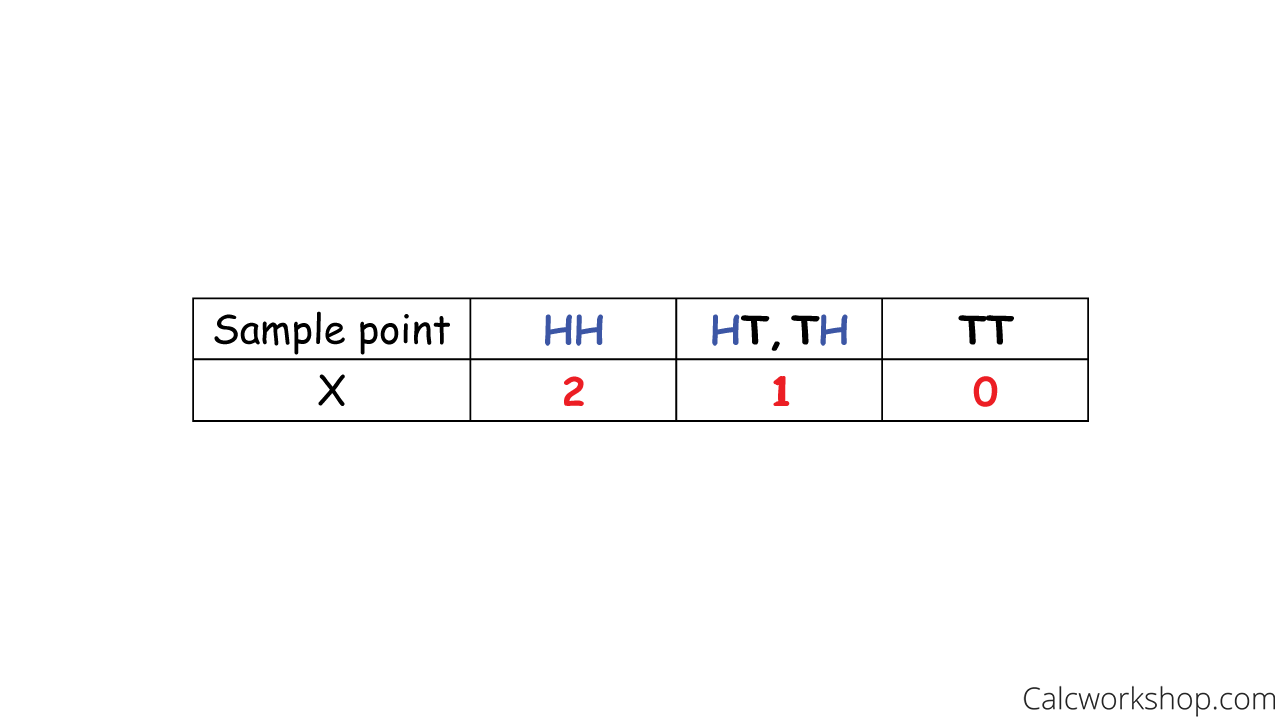
Random Heads Or Tails Variable
Now a random variable can be either discrete or continuous, similar to how quantitative data is either discrete (countable) or continuous (infinite). A random variable that takes on a finite or countably infinite number of values is called a Discrete Random Variable. A random variable that takes on a non-countable, infinite number of values is a Continuous Random Variable.
Here are a few real-life examples that help to differentiate between discrete random variables and continuous random variables.

Discrete Vs Continuous Variables
And this now leads us to the idea of Discrete Probability Distributions.
A discrete probability distribution lists all the possible values that the random variable can assume and their corresponding probabilities. So using our previous example of tossing a coin twice, the discrete probability distribution would be as follows.

Discrete Probability Distribution Example
What are the properties of a discrete probability distribution?
The set of all ordered pairs of (x, f(x)) is a probability function, also called a probability mass function (PMF), of the random variable X, if for each possible outcome.

Properties Of Discrete Probability Distribution
So, let’s look at these properties in action.
For example, let’s determine if the following probability distributions are discrete probability distribution.

Determine Whether the Distribution is a Discrete Probability Distribution
Likewise, we can use a probability distribution to find the probability of an event.
For example, given the following discrete probability distribution, we want to find the likelihood that a random variable X is greater than 4. All we have to do is determine the random variables that are true for this inequality, and sum their corresponding probabilities.
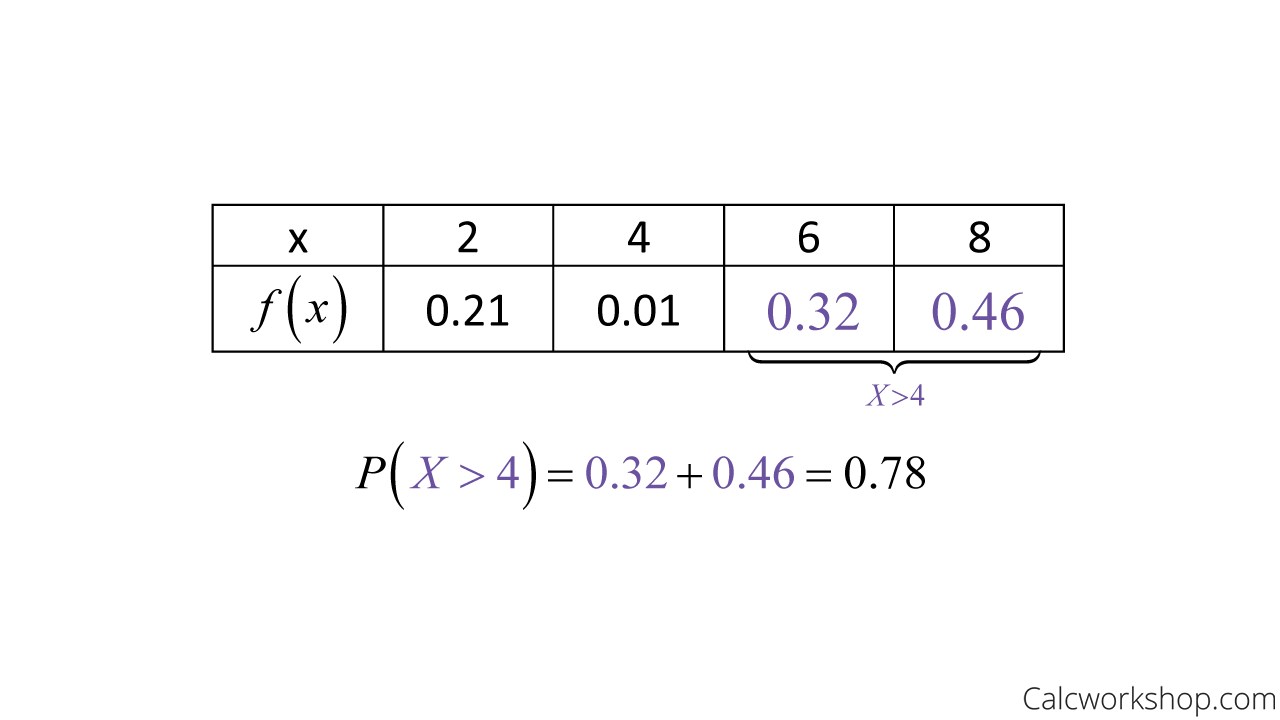
How To Find The Probability Distribution
But what if we want to compute the probability that the observed value of random variable X will be less than or equal to some real number x?
This is the concept of cumulative distributions!
If we define F(x) to be the Cumulative Distribution Function (CDF) of the random variable, then.

Cumulative Distribution Function Properties
Let’s look at an example.
Using our previous example, where we tossed a coin twice, let’s now find the cumulative distribution function (CDF)
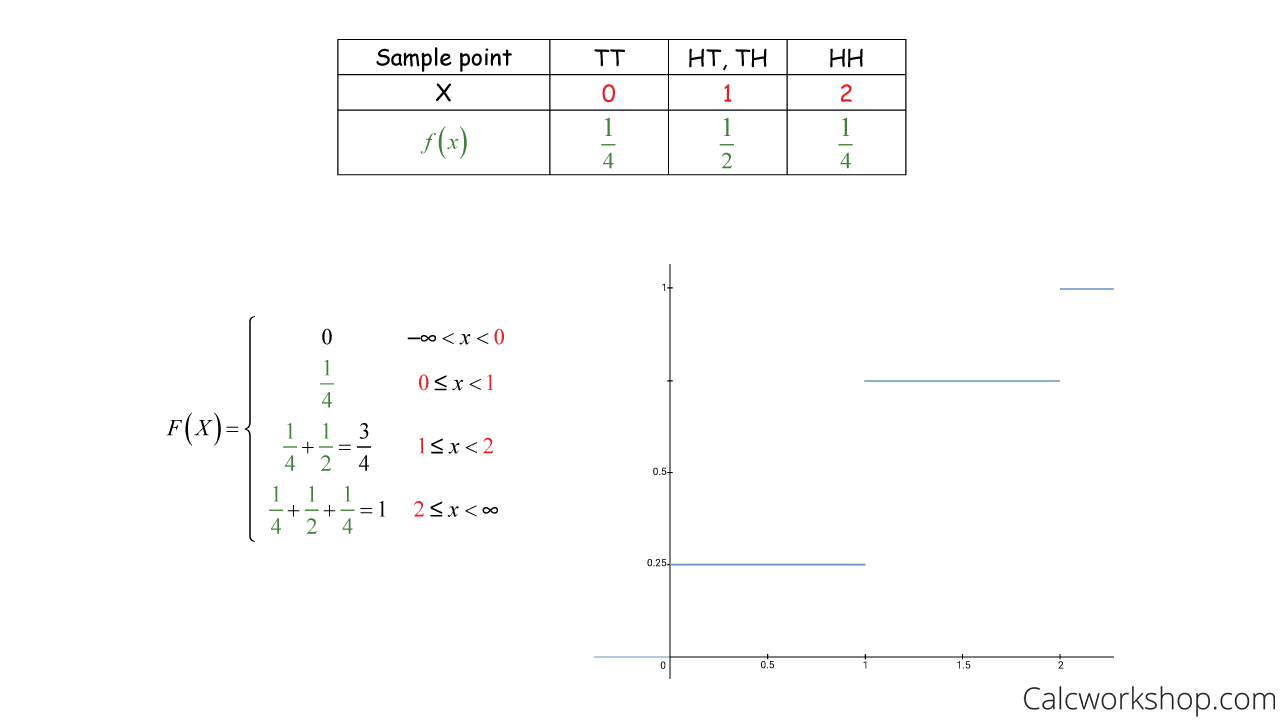
How To Find Cumulative Distribution Function
What’s important to note is that each jump’s magnitude is the exact probabilities in the probability distribution table!
As we proceed from left to right, notice that it looks like we are going upstairs. This demonstrates how the CDF is monotonically increasing!
Together, we will work through numerous examples of how to determine if a distribution is a probability distribution, identify probability given the probability mass function, create a discrete probability distribution for a sample set, and find the cumulative distribution function.
Let’s jump right in!
Discrete Random Variable – Lesson & Examples (Video)
1 hr 14 min
- Introduction to Video: Discrete Random Variables
- 00:00:29 – Overview of Discrete Random Variables, Continuous Random Variables, and Probability Distributions
- Exclusive Content for Members Only
- 00:13:17 – Find the probability distribution if a coin is tossed three times (Example #1)
- 00:19:30 – Determine if the given table is a probability distribution (Examples #2-4)
- 00:30:29 – Given the probability distribution find the probability of an event and create a histogram (Examples #5-8)
- 00:30:28 – Given the probability mass function find the probability of an event (Example #9)
- 00:34:03 – Construct a probability distribution for a carnival game (Example #10)
- 00:39:45 – Construct a tree diagram and find the probability for defective batteries (Example #11)
- 01:03:40 – Overview of Cumulative Distribution Functions with Example #12
- 01:12:49 – Find the cumulative function and obtain its graph (Example #13)
- 00:48:34 – Determine the probability function given the cumulative function (Example #14)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.