Did you know that the binomial distribution is built from the Bernoulli distribution?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
And wouldn’t it be nice if the probability, expectation, and variance were all pre-calculated for discrete random variables?
Well, for some essential discrete random variables, this is precisely the case.
Bernoulli Random Variable
The most straightforward kind of a random variable is called the Bernoulli Random Variable.
The Bernoulli random variable only has one independent trial; thus, it can only take one of two values – one and zero. A 1 means the experiment was a success, and a zero indicates the experiment failed. A Bernoulli random variable has the following properties:
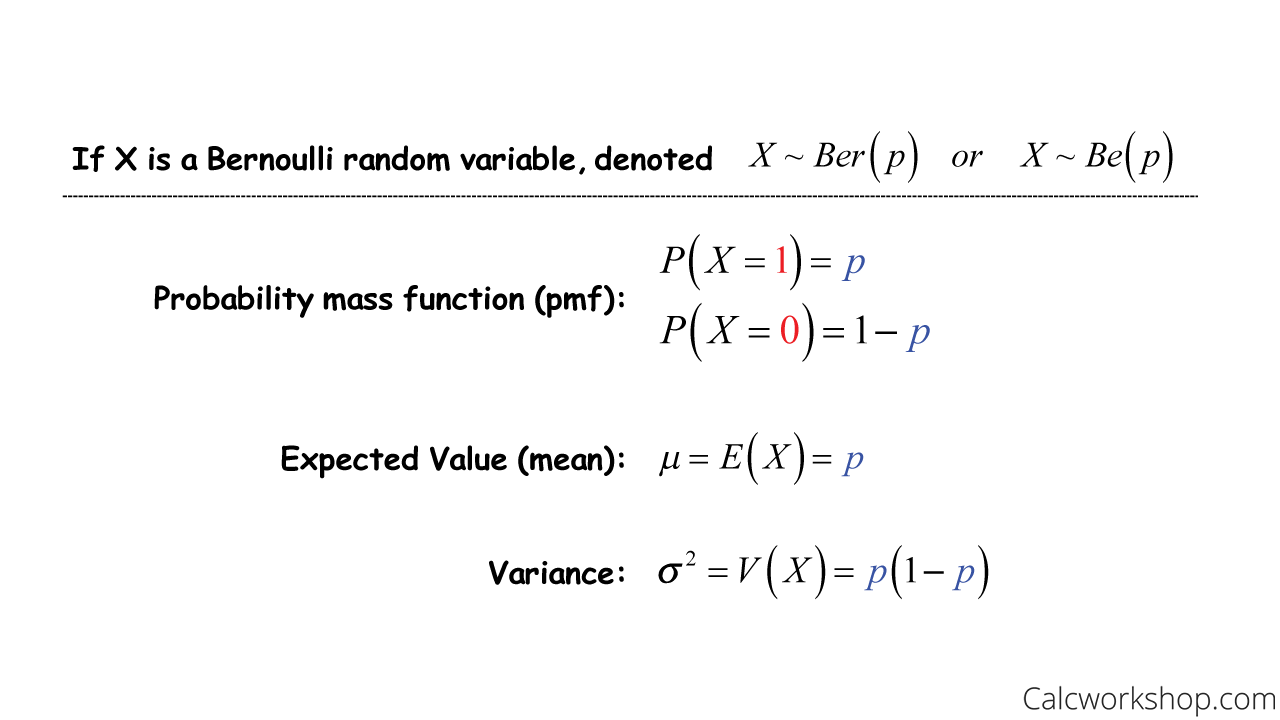
Bernoulli Distribution Mean And Variance
Worked Example
Let’s look at an example of a Bernoulli random variable.
Suppose we flip a coin only once. If it lands heads, then we win (success). But if it lands tails, then we lose (failure). This means that
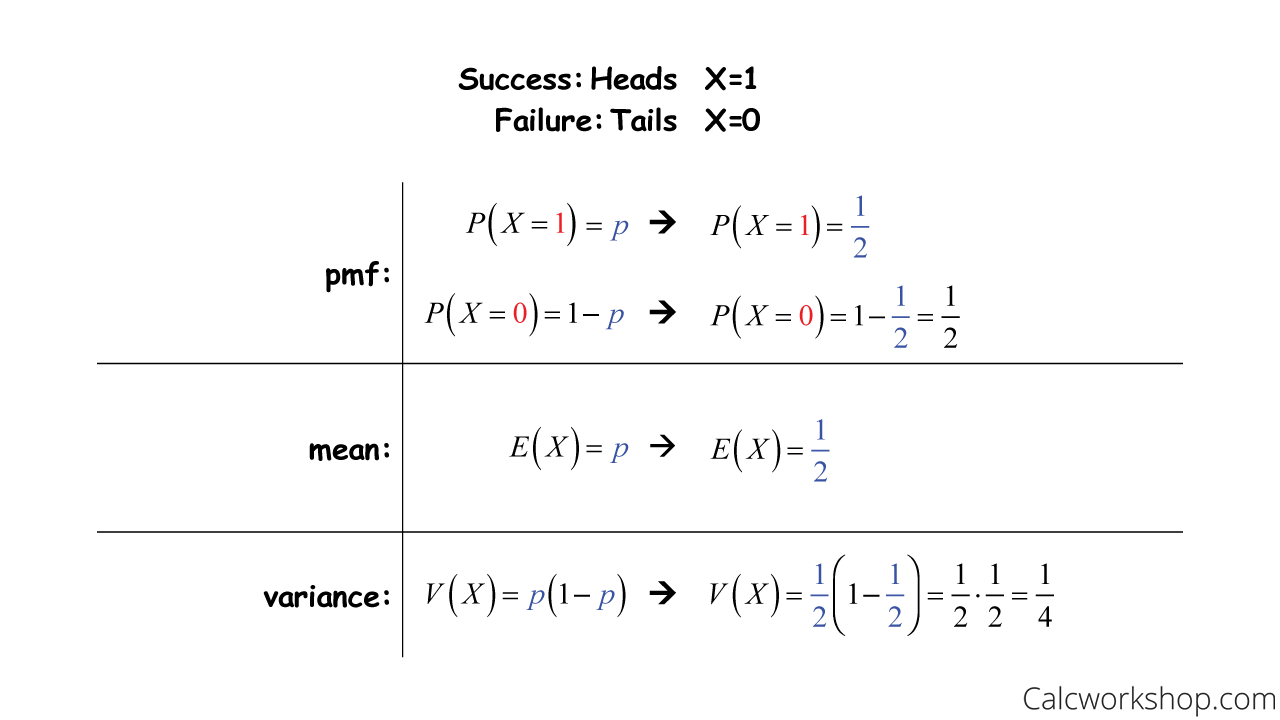
Bernoulli Distribution Example
As you can see, the Bernoulli random variable is exceptionally straightforward because there is only one independent trial (one flip of a coin, or one roll of a die).
Binomial Random Variable
But, what happens if you want to run the experiment or trial more than once?
Introducing the Binomial Random Variable!
A Binomial random variable represents the number of success in a fixed number of successive identical, independent trials, where each trial has the possibility of either two outcomes:
- Success
- Or Failure
Additionally, the probability of the two outcomes remains constant for every trial as defined in the NIST Handbook.
Here’s an easy way to remember the conditions of a Binomial distribution: BINS!

Binomial Distribution Rules Mnemonic
Worked Example
So, let’s see how we use these conditions to determine whether a given random variable has a binomial distribution.
For example, suppose we shuffle a standard deck of cards, and we turn over the top card. We put the card back in the deck and reshuffle. We repeat this process five times. Let X equal the number of Jacks we observe. Is this a binomial distribution?
All we have to do is check the BINS!
- B – binary – yes, either it’s a Jack or it isn’t
- I – independent – yes, because we replace the card each time, the trials are independent.
- N – number of trials fixed in advance – yes, we are told to repeat the process five times.
- S – successes (probability of success) are the same – yes, the likelihood of getting a Jack is 4 out of 52 each time you turn over a card.
Therefore, this is an example of a binomial distribution.
Okay, so now that we know the conditions of a Binomial Random Variable, let’s look at its properties:
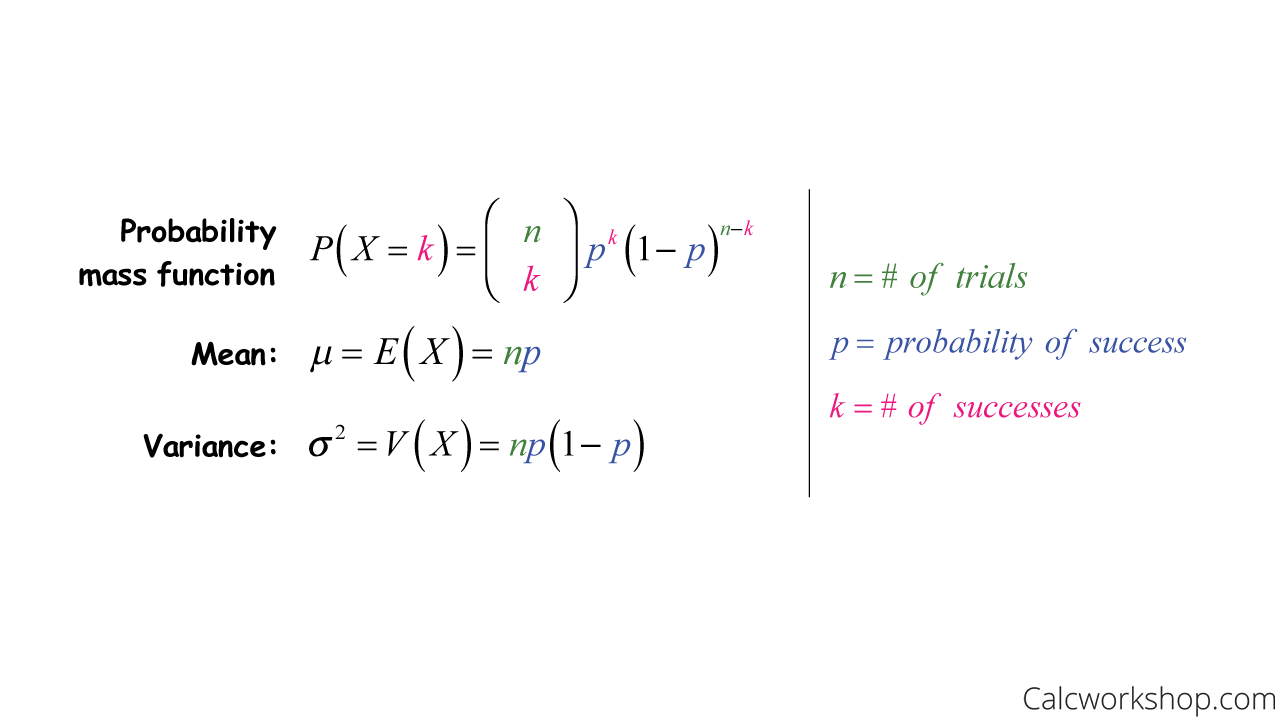
Mean And Variance Of Binomial Distribution
Worked Example
Let’s investigate how to use the properties with an example.
Suppose that Charlie makes a free throw 0.82 on any one try. Assuming that this probability doesn’t change, find the chance that Charlie makes 4 out of the next seven free throws.

Binomial Probability Example
This means that Charlie has a 0.0923 chance of making precisely 4 out of the next seven free throws.
And using the same example, let’s determine the number of free throws Charlie should expect to make and the standard deviation.
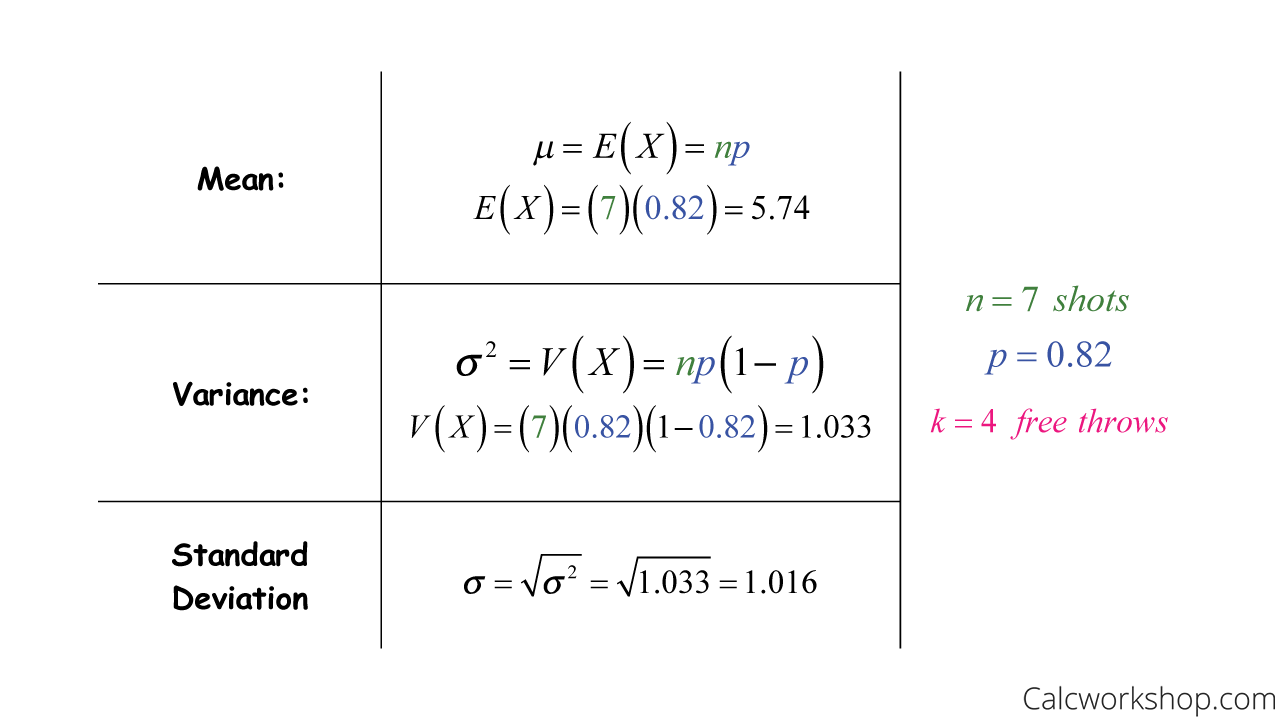
Mean Variance Standard Deviation For A Binomial Problem
What this shows us is that we would expect Charlie to make about 5.74 free throws out of 7 shots, with a standard error of 1.016.
Throughout this video, we will utilize our conditions for binomial random variables and apply our properties to find expectancy, variance, and probabilities of binomial distributions.
Binomial Distribution – Lesson & Examples (Video)
1 hr 12 min
- Introduction to Video: Bernoulli and Binomial Random Variables
- 00:00:30 – Bernoulli Distribution Overview with Examples #1-2
- Exclusive Content for Members Only
- 00:11:12 – Binomial Distribution Overview
- 00:21:18 – Determine if the random variable represents a binomial distribution (Examples #3-6)
- 00:32:11 – Find the probability, expected value, and variance for the binomial distribution (Examples #7-8)
- 00:45:58 – Find the probability and cumulative probability, expected value, and variance for the binomial distribution (Examples #9-10)
- 00:59:12 – Find the cumulative probability, expected value, and variance for the binomial distribution (Example #11)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.