There are some differential equations for which we are unable to solve algebraically.
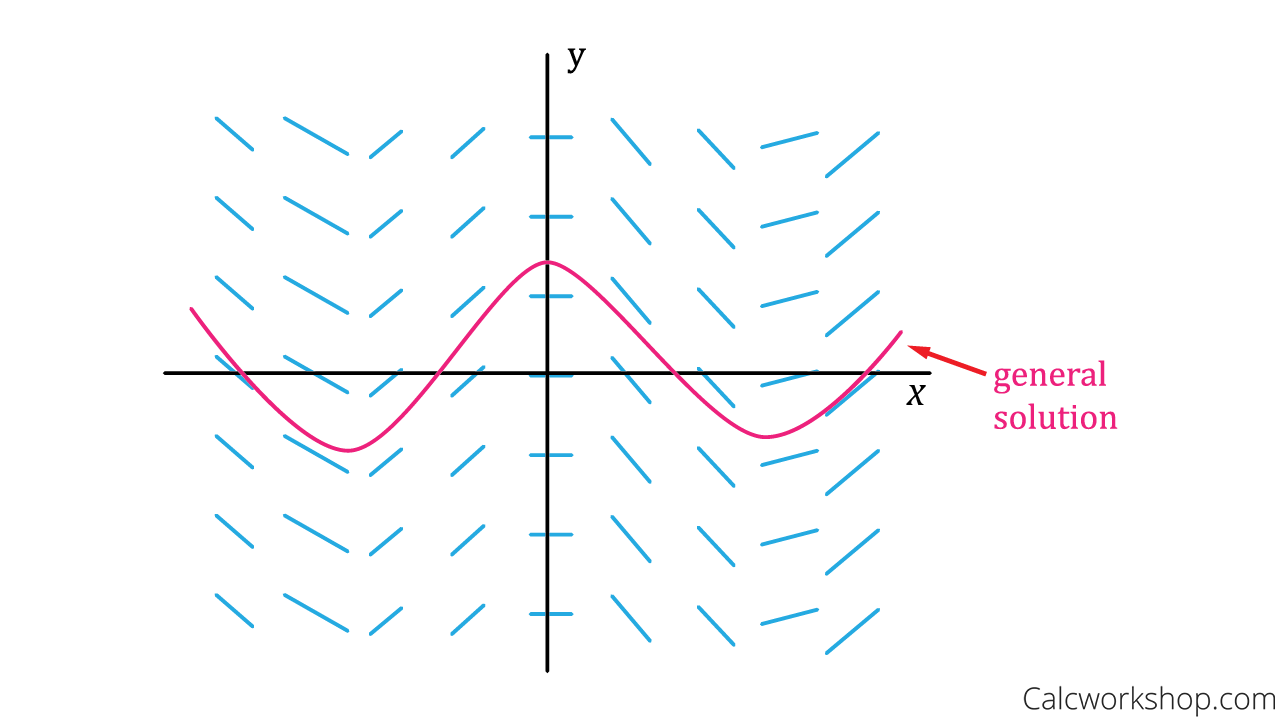
Identifying the General Solution of a Slope Field
In these instances, we must rely on a numerical approach or a graphical approach.
A Slope Field, sometimes called a Direction Field, is a way for us to analyze a function by looking at the graph of its slope.
While an explicit solution is not attainable, we are still able to generate a solution curve by observing how the slope of the function is behaving at specific points.
As Wikipedia points out, a slope field is useful because it can be created without solving the differential equation analytically, and can be used to qualitatively visualize or approximate solutions.
So if we draw short line segments that portray the slope of the curve at several different points, the result is called a slope field, or directional field.
And these line segments indicate the direction in which the solution curve is heading, and help us to visualize the overall shape of the curve without having to solve the differential equation!
Together, we’ll learn how to create a slope field and draw a particular solution through a given condition.
Slope Fields Video

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.