How do you solve related rates?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question!
And that’s just what you’re going to learn how to do in today’s calculus lesson.
Let’s go!
What Are Related Rates (Real Life Examples)
Have you ever watched a baseball player who is rounding third and heading for home and wondered if they had enough speed to make it before getting tagged out by the thrower?
Or have you ever watched a basketball player shoot a free-throw and speculate if the ball has enough height and distance?
Or perhaps you’ve listened to a guitar solo and contemplated the number of vibrations per second needed to make the guitar strings hum at the perfect pitch?
If you have, and even if you haven’t, all of these queries have something in common — something is changing with respect to time.
This is the idea behind related rates.
The baseball player’s distance to the home plate is changing with respect to the runner’s speed per second. The success of a free-throw is related to the ball’s projectile motion and the instantaneous rate of change of the height and distance traveled. And when a guitar string is plucked, the rate of the guitar string’s vibration (frequency) produces high or low pitches, which make the music we hear sound pleasing.
What Does It Mean If Two Rates Are Related
Let’s make sense of things using the image to the right.
Imagine a person is outside looking up into the sky and they spot an airplane that is flying at an altitude of 6 miles above the ground. Now, as the plane continues on its flight path, several things are changing with respect to each other.
The angle of elevation (theta), the line of sight (hypotenuse), as well as the horizontal distance are all changing as the plane flies overhead and with respect to time.
And that’s what it means for two or more rates to be related — as one rate changes, so does the other.
Calculate the Speed of an Airplane
How To Solve Related Rates Problems
We use the principles of problem-solving when solving related rates. The steps are as follows:
- Read the problem carefully and write down all the given information.
- Sketch and label a graph or diagram, if applicable.
- Find an equation that relates the unknown variable and known variable(s) by looking for geometric shapes, known formulas, ratios such as the Pythagorean theorem, area and volume formulas, or trig identities.
- Simplify using appropriate substitutions, so that chosen equation has only two variables (known and unknown).
- Differentiate the equation implicitly with respect to time.
- Substitute all known values into the derivative and solve for the final answer.
Ex) Cone Filling With Water
Alright, so now let’s put these problem-solving steps into practice by looking at a question that frequently appears in AP calculus, college, and university classes — the cone problem.
If water is being pumped into the tank at a rate of 3 cubic feet per second, find the rate at which the water level is rising when the water is 4ft deep.
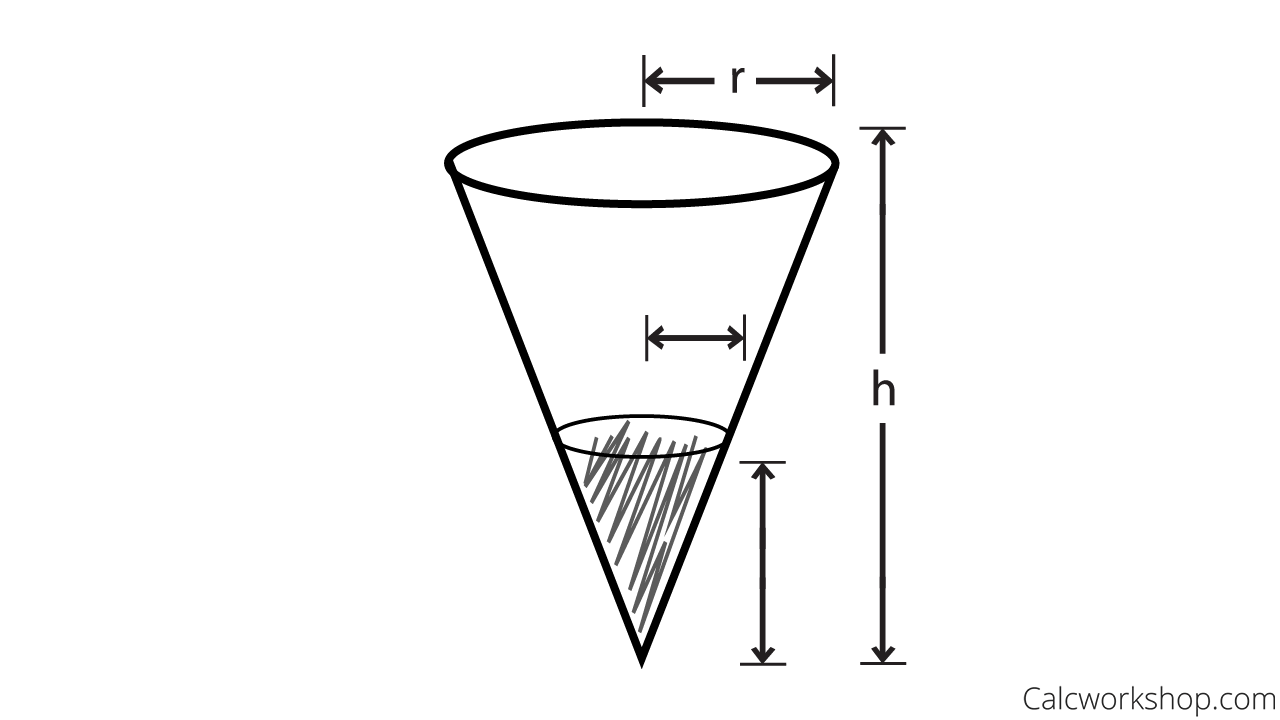
Related Rates – How Things Change Over Time
Steps 1 & 2: Read and Sketch
First, we will sketch and label a cone, vertex down, and identify all pertinent information.
\begin{equation}
\frac{d V}{d t}=3^{f t^{3}} / \mathrm{sec}
\end{equation}
\begin{equation}
\frac{d h}{d t}=?
\end{equation}
\begin{equation}
h=4 f t
\end{equation}
Related Rates — Cone Problem
Step 3: Find An Equation That Relates The Unknown Variables
Because we were given the rate of change of the volume as well as the height of the cone, the equation that relates both V and h is the formula for the volume of a cone.
\begin{equation}
V=\frac{1}{3} \pi r^{2} h
\end{equation}
But here’s where it can get tricky. Our equation has three variables (V, r, and h), but we only have two derivatives, dh, and dV.
Hmmm, that means we have to reduce the number of variables so that the number of variables equals the number of derivatives.
How does that work?
Step 4: Simplify To Get Known & Unknown Variables
We use an incredibly useful ratio found by the similar triangles created from the cone above (HINT: this ratio will be used quite often when solving related rate problems). And in so doing, we will also create a proportion, using the conical tank’s original dimensions, and solve for r. This way, we can eliminate the r in volume formula.
\begin{equation}
\frac{r}{h}=\frac{3}{5}
\end{equation}
\begin{equation}
r=\frac{3}{5} h
\end{equation}
\begin{equation}
V=\frac{1}{3} \pi\left(\frac{3}{5} h\right)^{2} h=\frac{3}{25} \pi h^{3}
\end{equation}
\begin{equation}
V=\frac{3}{25} \pi h^{3}
\end{equation}
Step 5: Implicit Differentiation
We will now use implicit differentiation on both sides with respect to t.
\begin{equation}
V=\frac{3}{25} \pi h^{3}
\end{equation}
\begin{equation}
\frac{d V}{d t}=\frac{9}{25} \pi h^{2}\left(\frac{d h}{d t}\right)
\end{equation}
Step 6: Substitute Back In
And lastly, we will substitute our given information and solve the unknown rate, dh/dt.
\begin{equation}
\frac{d V}{d t}=\frac{9}{25} \pi h^{2}\left(\frac{d h}{d t}\right) \text { when } \frac{d V}{d t}=3 \text { and } h=4
\end{equation}
\begin{equation}
3=\frac{9}{25} \pi(4)^{2}\left(\frac{d h}{d t}\right)
\end{equation}
\begin{equation}
\frac{d h}{d t}=\frac{25}{48 \pi}
\end{equation}
See, all we have to do is follow the steps and arrive at our answer!
And don’t worry, we will do two more cone problems in the video below, so you’ll become a master at these questions in no time!
Let’s get after it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 35 min
Ladder Sliding Down Wall
- Overview of Related Rates + Tips to Solve Them
- 00:02:58 – Increasing Area of a Circle
- 00:12:30 – Expanding Volume of a Sphere
- 00:21:15 – Expanding Volume of a Cube
- 00:26:32 – Calculate the Speed of an Airplane
- 00:39:13 – Conical Sand Pile
- 00:51:19 – Conical Water Tank
- 00:59:59 – Boat & Winch
- 01:09:13 – Ladder Sliding Down A Wall
Related Rates
Related Rates – 2 Examples
Get access to 6 more examples and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.