Wouldn’t it be nice to be able to calculate the slope of the tangent quickly and easily?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Thankfully we have the power rule to simplify our work tremendously, for it allows us to take derivatives of functions without needing to labor over the formal limit definition.
What Is The Power Rule
Okay, so what is the power rule, and how do we use it?
The power rule is used to find the slope of polynomial functions and any other function that contains an exponent with a real number. In other words, it helps to take the derivative of a variable raised to a power (exponent).
The Steps
All we have to do is:
- Move the exponent down in front of the variable.
- Multiply it by the coefficient.
- Decrease the exponent by 1.
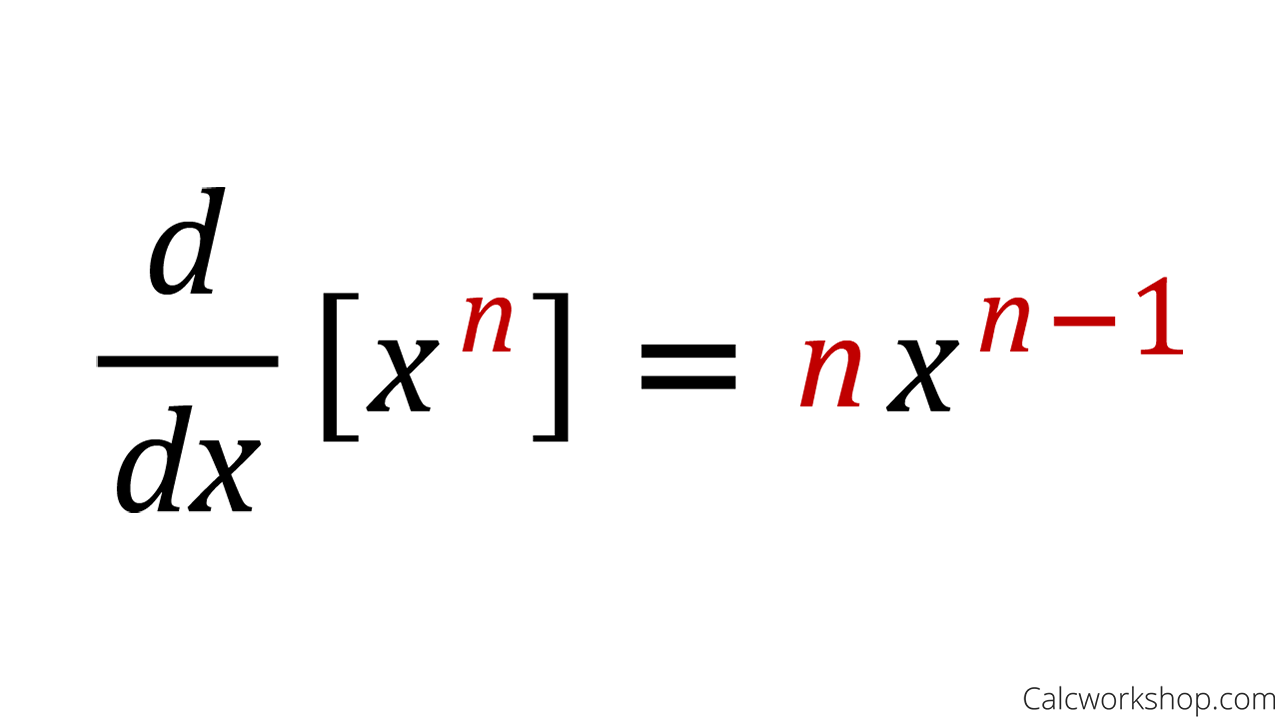
General Version Of The Power Rule
Ex) Derivative of
For instance, let’s use the power rule to find the derivative of x^2. All we have to do is bring the exponent down in front and then decrease the exponent by 1.
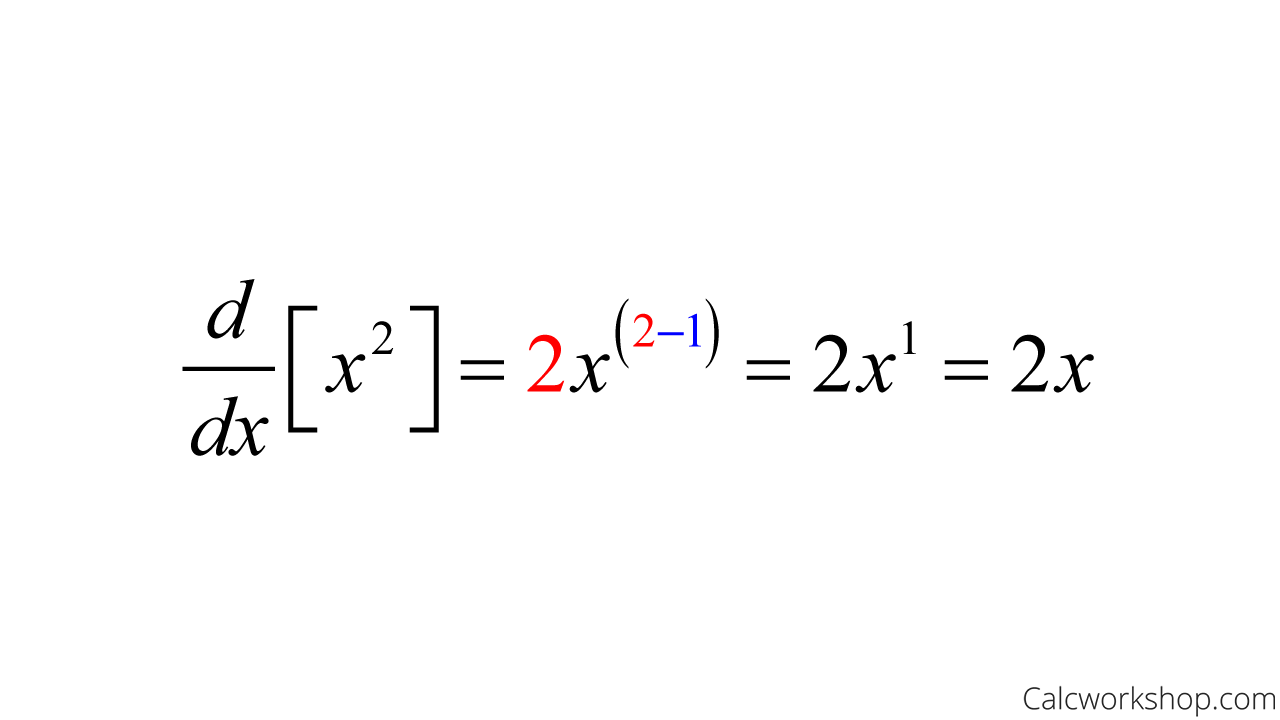
Derivative Of X^2
So, the derivative of x^2 is 2x!
But how does the power rule apply to more complicated functions?
Well, it’s important to note that we can apply the power rule to any function that contains terms that are the product of a real number, a coefficient, and a variable raised to a real number. These functions are called power functions.
Simply put, the power rule lends itself to the following differentiation rules:
- Constant Multiple Rule
- Derivative of a Constant Function
- Sum and Difference Rule
Which help us to find the rate of change of more “complicated” power functions.
Let’s look at each of these differentiation rules more closely as we learn to apply our general power rule.
Constant Multiple Rule
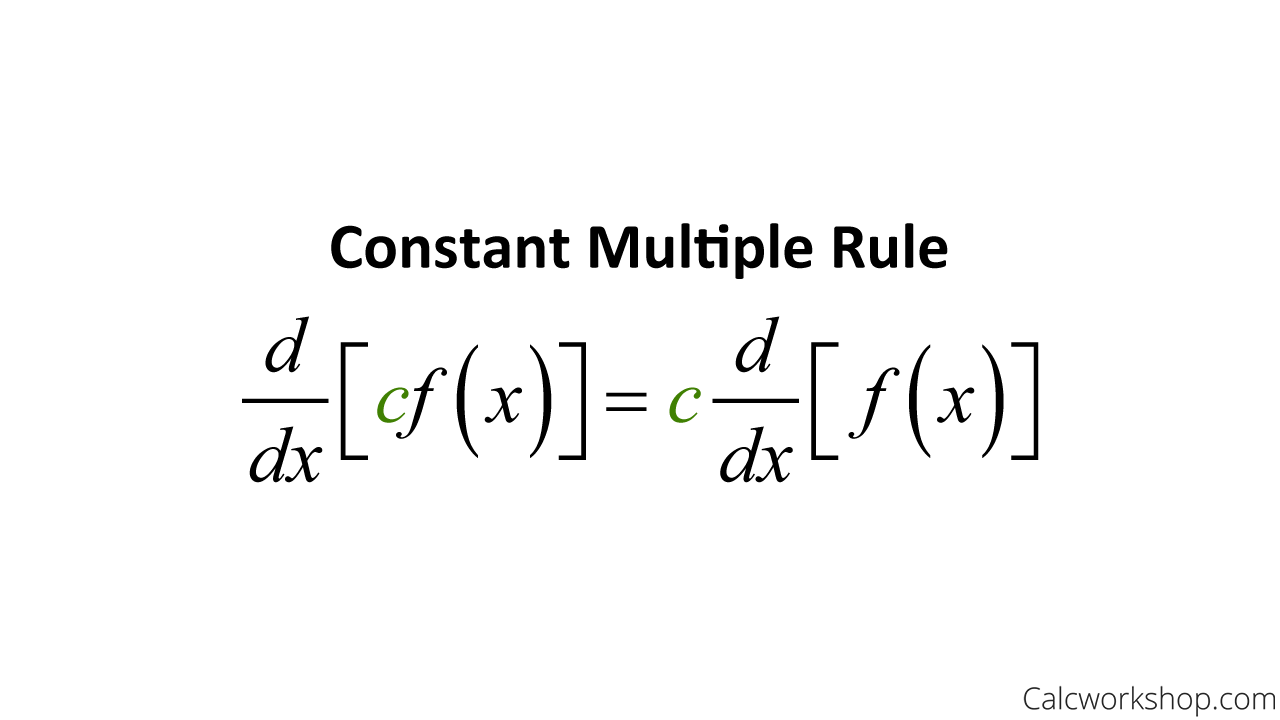
Constant Multiple Rule
Ex) Derivative of
For instance,
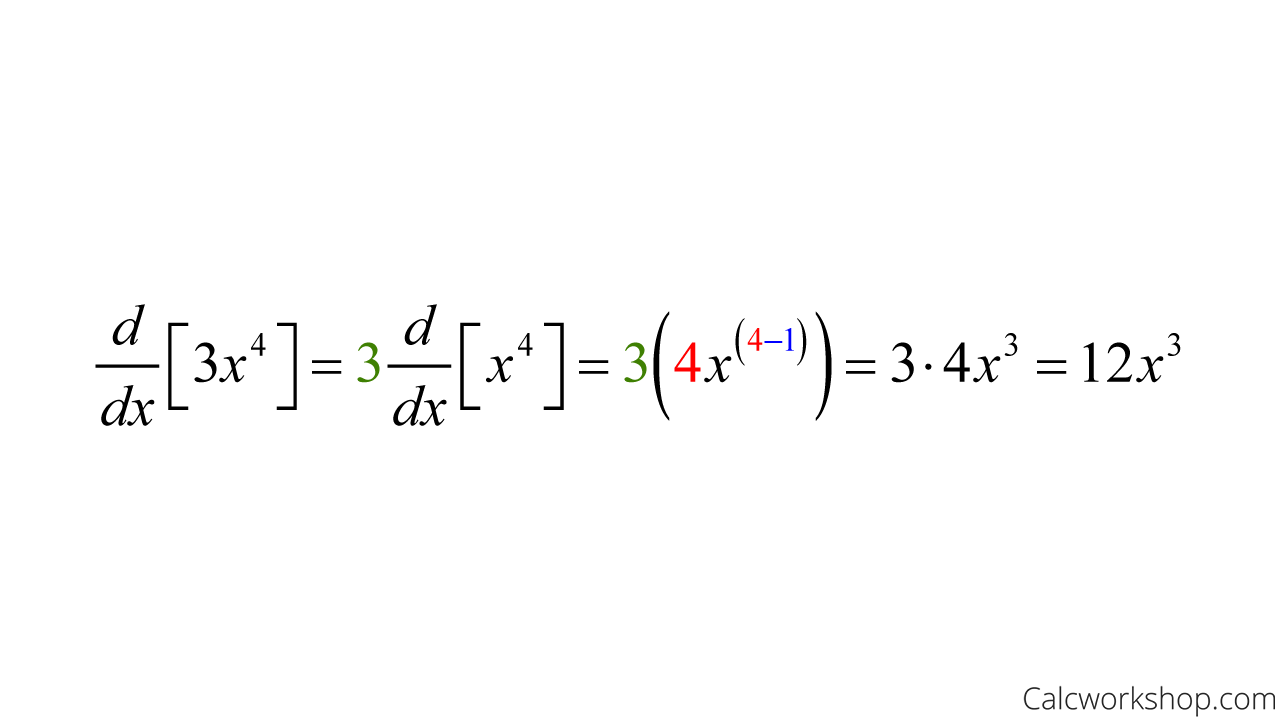
Derivative Constant Multiple Rule — Example
Derivative Of A Constant

Derivative Constant Rule
Why?
Because constants are terms that contain only numbers, specifically, they are terms without variables. So, how do we apply the power rule when there isn’t a variable or exponent to bring down?
Ex) Derivative of 4
By recognizing that the unseen variable has an exponent of zero, as seen in the example below!
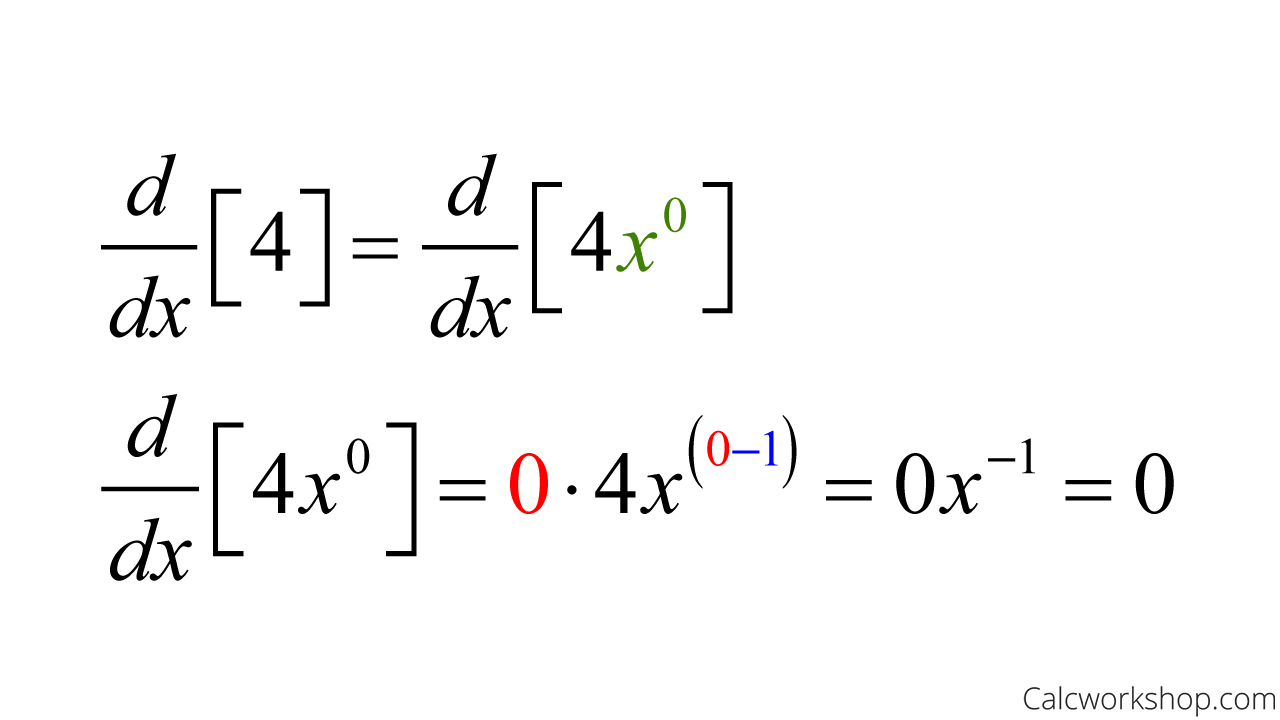
Derivative Of A Constant To A Power — Example
But do we have to show all of these steps each time we have a constant term?
Nope. Now that we know why it works, all we have to do is apply the rule. This means, every time you take the derivative of a constant, the answer is zero.
Sum And Difference Rules

Derivative Sum Difference — Formula
This rule states that we can apply the power rule to each and every term of the power function, as the example below nicely highlights:
Ex) Derivative of
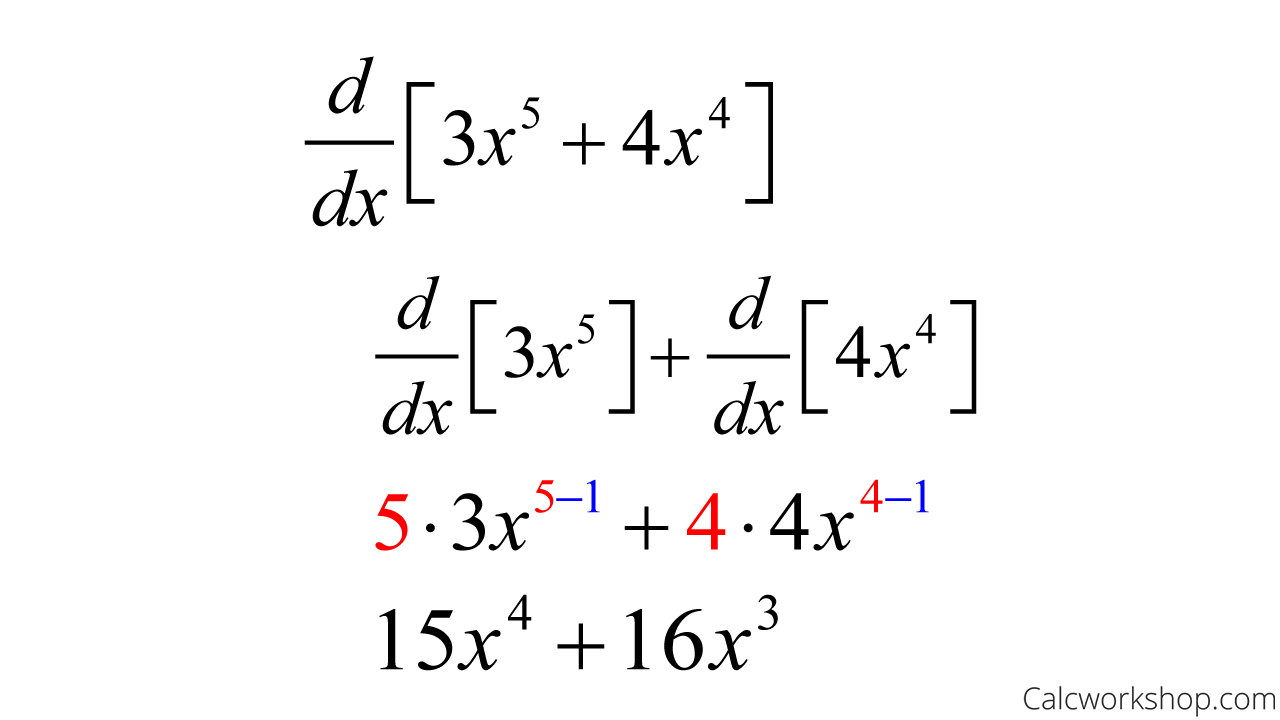
Derivative Sum Rule — Example
See, the power rule is super easy to use!
But did you know that we can apply the power rule and its corollaries to functions other than polynomials, such as functions containing negative or rational exponents?
Extended Power Rule
Let’s look at a few more examples to get a better understanding of the power rule and its extended differentiation methods.
Use the power rule to differentiate each power function.
Ex) Derivative of

Derivative Of A Negative Power — Example
Ex) Derivative of
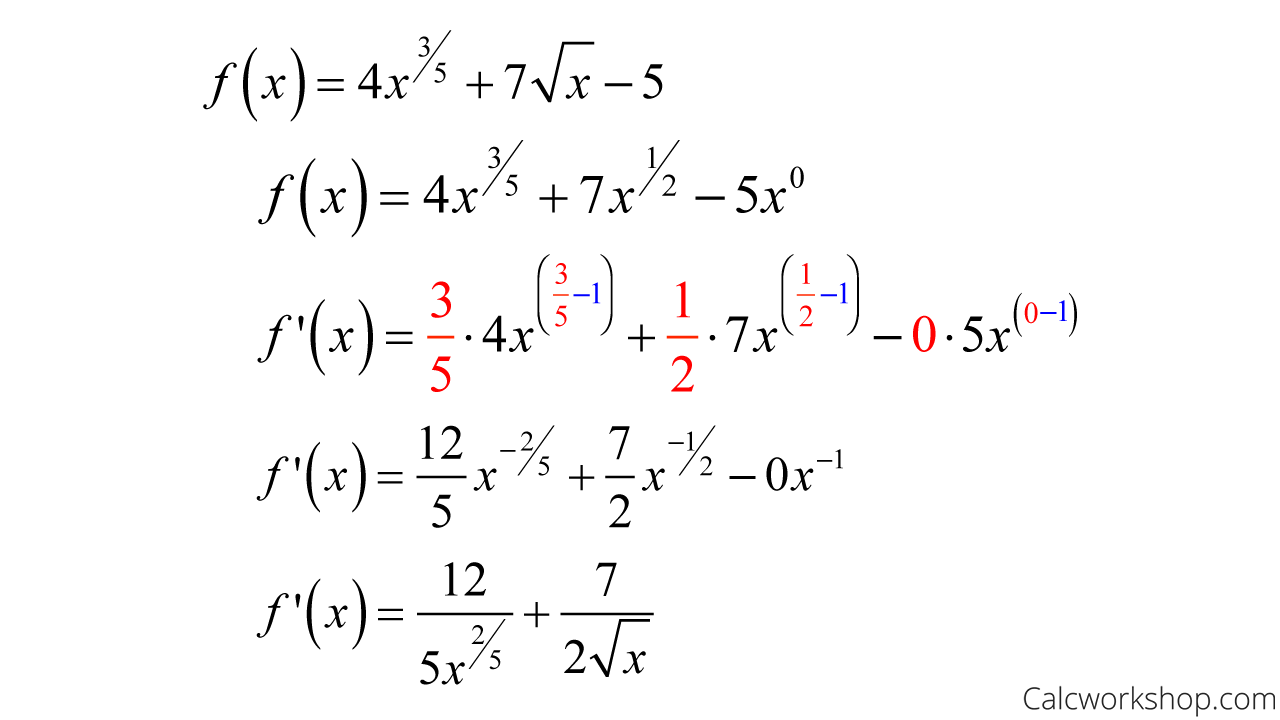
Find Derivative Rational Exponents — Example
Summary
Isn’t the power rule fantastic?
No wonder why it is considering one of the most important rules in all of differentiation, according to Wikipedia.
Together we will walk through 10 examples in detail, and I’m confident that you will think the power rule is pretty powerful too!
Let’s jump in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.