Suppose you are asked to approximate a root of an equation.
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What do you do?
Well, you know that a root is synonymous with x-intercept, so you are being asked to find where the function crosses the x-axis. This means you need to set your equation equal to zero and solve for x.
That seems easy enough, right?
Now that might be a problem, because sometimes — finding the exact solution (roots) of an equation algebraically is easier said than done.
So when faced with solving an equation that seems impossible, we need this method!
Why?
Newton’s Method, also known as Newton Raphson Method, is important because it’s an iterative process that can approximate solutions to an equation with incredible accuracy. And it’s a method to approximate numerical solutions (i.e., x-intercepts, zeros, or roots) to equations that are too hard for us to solve by hand.
How To Use Newton’s Method
The idea behind is to start with an initial guess which is reasonably close to the true root (solution) and then to use the tangent line to obtain another x-intercept that is even better than our initial guess or starting point.
Let’s look at this conceptually to make sense of what is happening.
Assume we want to find the root (i.e., x-intercept) for f(x). This means we want to find a in the picture below.
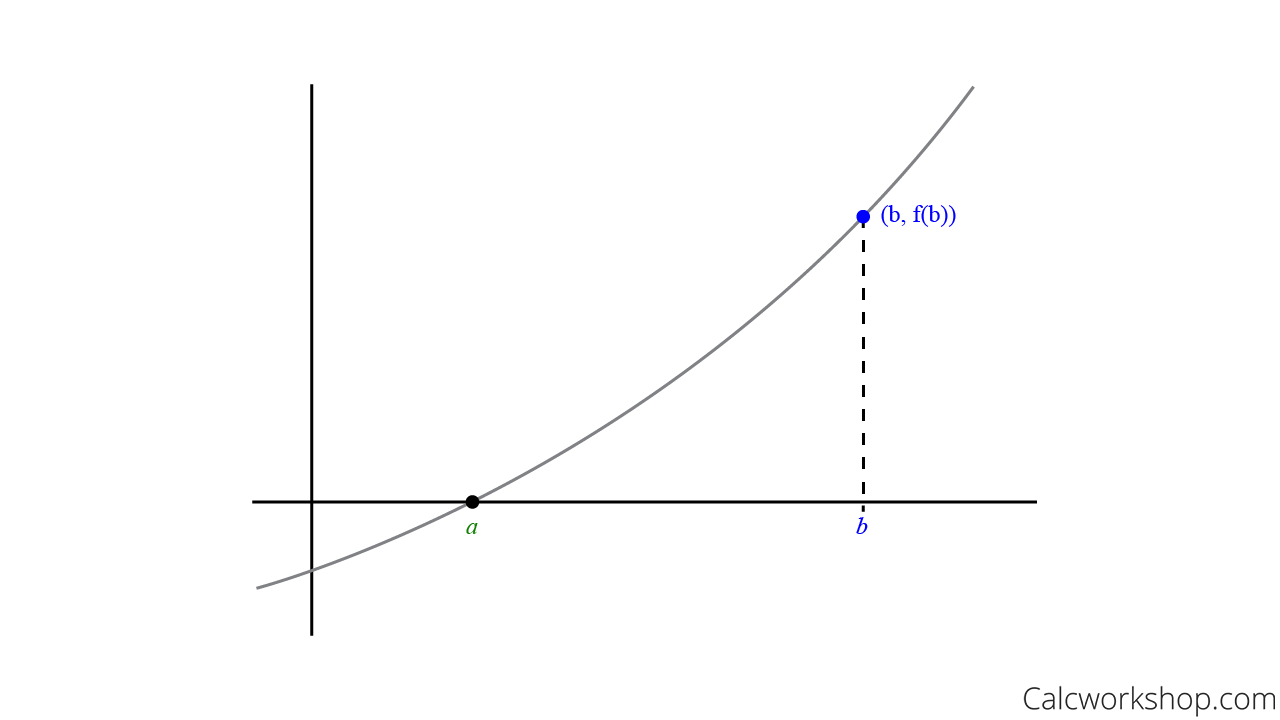
Step One: Approximate Point B
So, we begin with an initial guess (as noted by UC Davis) that is relatively close to point a, which is indicated as point b, and substitute b into f(x) and see if it equals zero. If it does equal, we’re done. However, more than likely, this will not be the case, and we will need to try for a better guess.
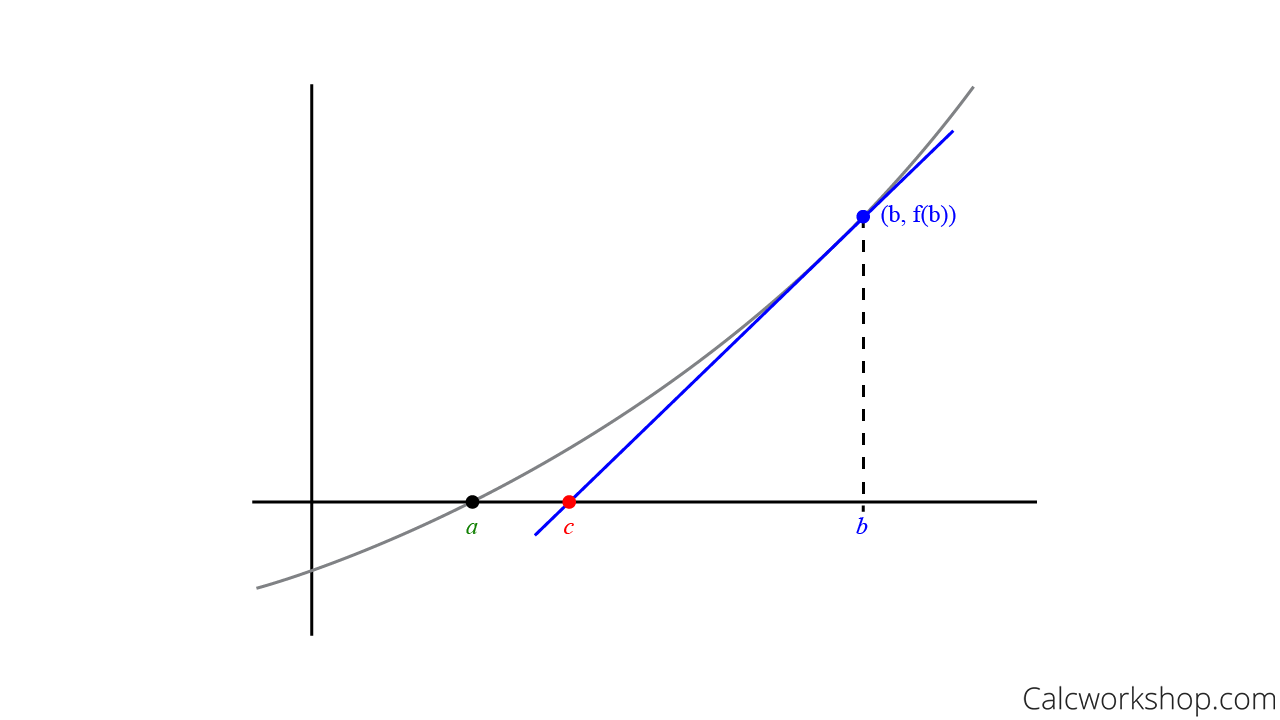
Step Two: Drawing Tangent Lines For B
How?
By using our knowledge of linear approximation. If we can create a tangent line to the graph at point b, then we can find another point even closer to a that also intersects the x-axis, at point c, as seen below.
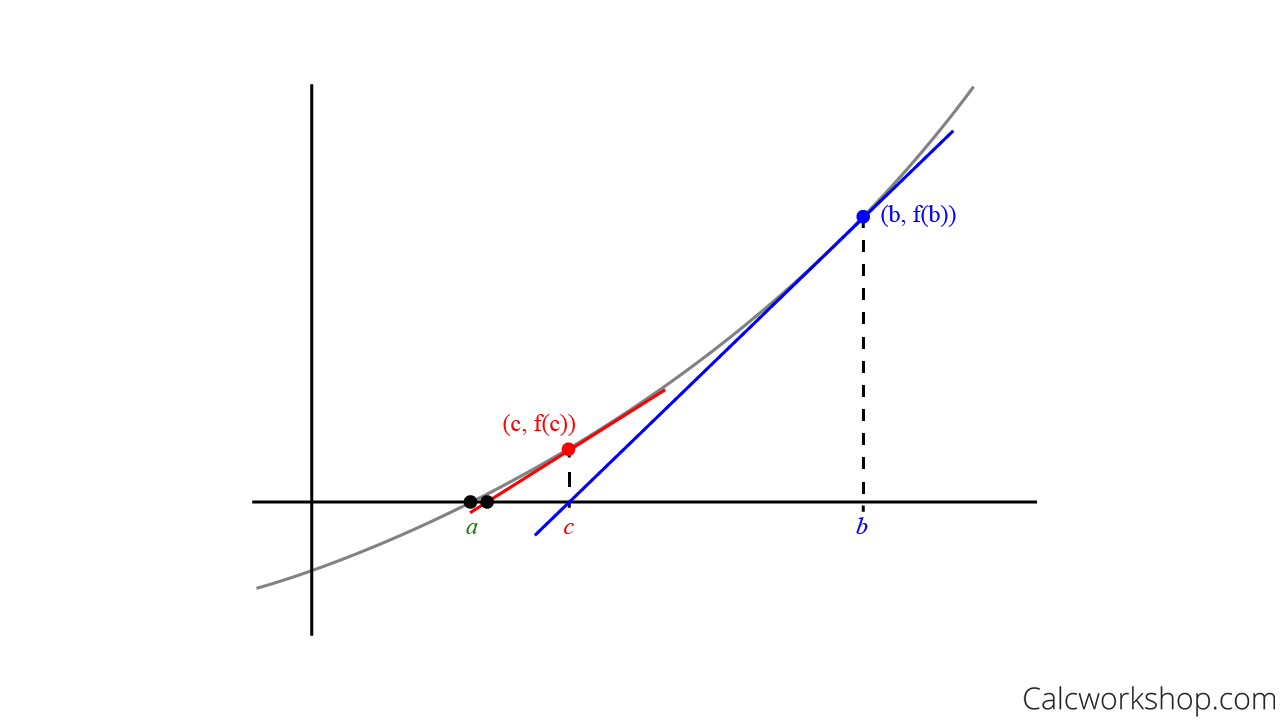
Step Three: Find The Tangent Line At C
And we keep using this process until we can find two successive values that agree to the desired decimal place.
In other words, until we finally converge on the value of a.
This iterative process is called Newton’s Method!
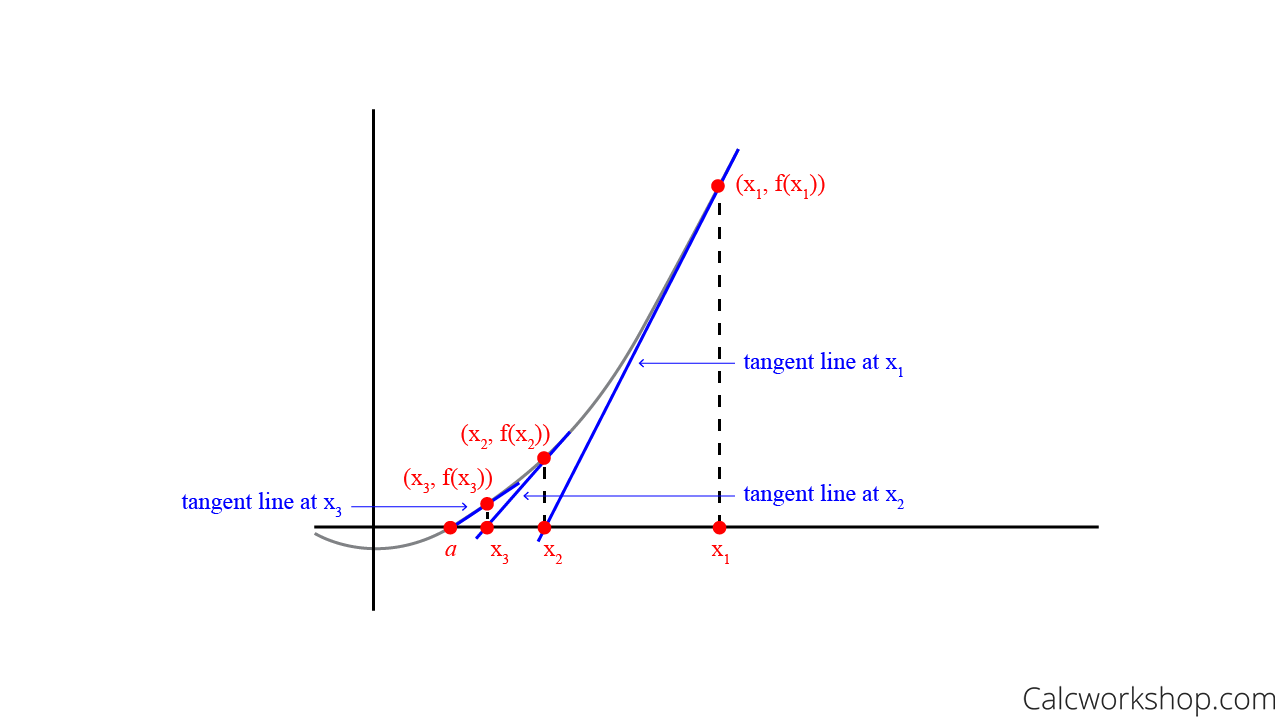
Newton’s Method — Calculus
Newton’s Method Formula
And to help with our calculations, we can use the following formula:
If the nth approximation is \(x_{n}\) and \(f^{\prime}\left(x_{n}\right) \neq 0\), then the next approximation is given by:
\begin{equation}
x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)}
\end{equation}
Example
Alright, let’s work through a problem together.
Use Newton’s Method, correct to eight decimal places, to approximate \(\sqrt[7]{1000}\).
First, we must do a bit of sleuthing and recognize that \(\sqrt[7]{1000}\) is the solution to \(x^{7}=1000\) or \(x^{7}-1000=0\).
Therefore, our function for which we will use is \(f(x)=x^{7}-1000\).
Next, we will calculate the first derivative and substitute both the function and derivative into our formula.
\begin{equation}
\begin{array}{l}
f^{\prime}=7 x^{6} \\
x_{n+1}=x_{n}-\frac{x_{n}^{7}-100}{7 x_{n}^{6}}
\end{array}
\end{equation}
Now it’s time to guess a reasonably comparable value to the actual value. So, let’s say \(x_{1}=3\).
And now it’s time to perform our iterations until we find two numbers that are the same up to eight decimal places.
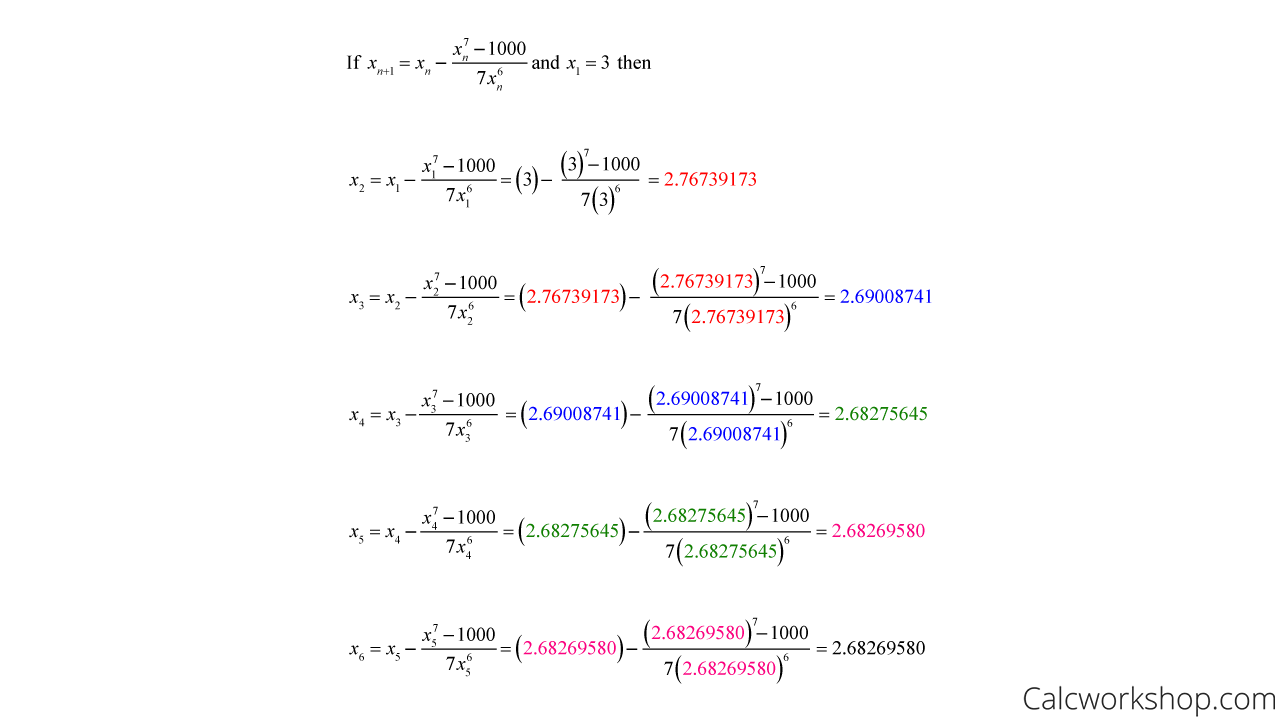
Newton’s Method — Example
So, after six iterations, we have found that the seventh root of 1000 to be approximately 2.6826958.
And that’s all you have to do.
Cool, right?
Summary
And did you know that Newton’s Method is more than just a root finder. It’s also effective for finding critical numbers, absolute minimums and maximums, coordinates of inflection points, and so much more.
Together we will walk through several examples, in great detail, so we can become human calculators and wield this new superpower.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.