Wouldn’t it be nice to be able to find the limit of an indeterminate form quickly and easily without having to use the conjugate or trig identities?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great news!
Because that’s exactly what L’Hopital’s Rule is for.
Our foundational rule for taking limits is not difficult – plug the number into the function and simplify.
But for some functions, this yields a value of zero over zero or infinity over infinity or one of the other indeterminate forms, as seen below.

7 Indeterminate Forms
This is called an indeterminate form, and we must transform our given function to evaluate the limit correctly.
In our limits section we discussed techniques for evaluating limits of indeterminate forms, such as
- Factoring
- Common Denominators
- Conjugate Pairs
- Trig Identities
- Horizontal Asymptotes For Limits At Infinity
But sometimes, even these methods can be challenging to implement.
Thankfully, now that we are familiar with derivatives, we can learn a new tool for evaluating indeterminate limits!
When Can You Use L’hopital’s Rule
We can apply L’Hopital’s rule, also commonly spelled L’Hospital’s rule, whenever direct substitution of a limit yields an indeterminate form.
L’Hospital’s Rule states:
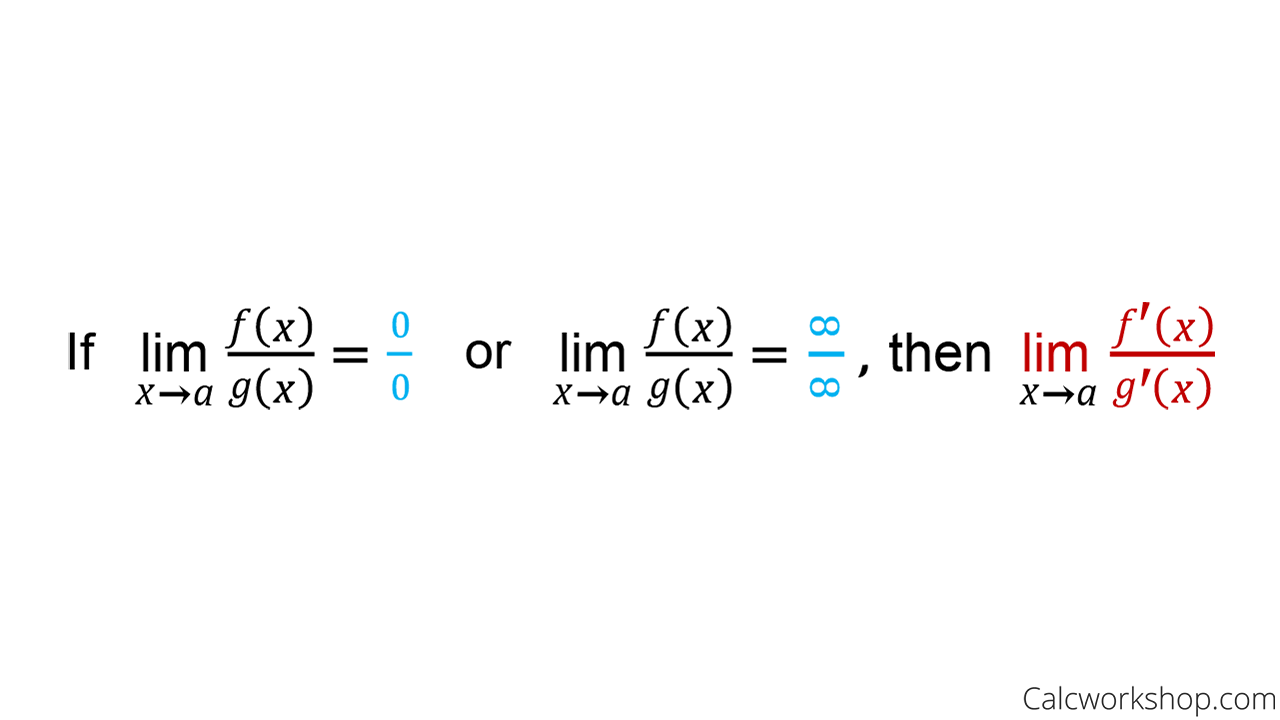
L’Hopital’s Rule for Indeterminate Forms
This means that the limit of a quotient of functions (i.e., an algebraic fraction) is equal to the limit of their derivatives.
It is important to note that L’Hopital’s rule treats f(x) and g(x) as independent functions, and it is not the application of the quotient rule.
How To Use L’hopital’s Rule
We differentiate the numerator and the denominator separately and then take the limit.
Additionally, I would like to point out that there will be times when L’Hopital’s rule must be applied more than once to calculate the limit value successfully.
Example
Let’s look at how we apply l’Hoptial’s rule for the indeterminate form of zero over zero.
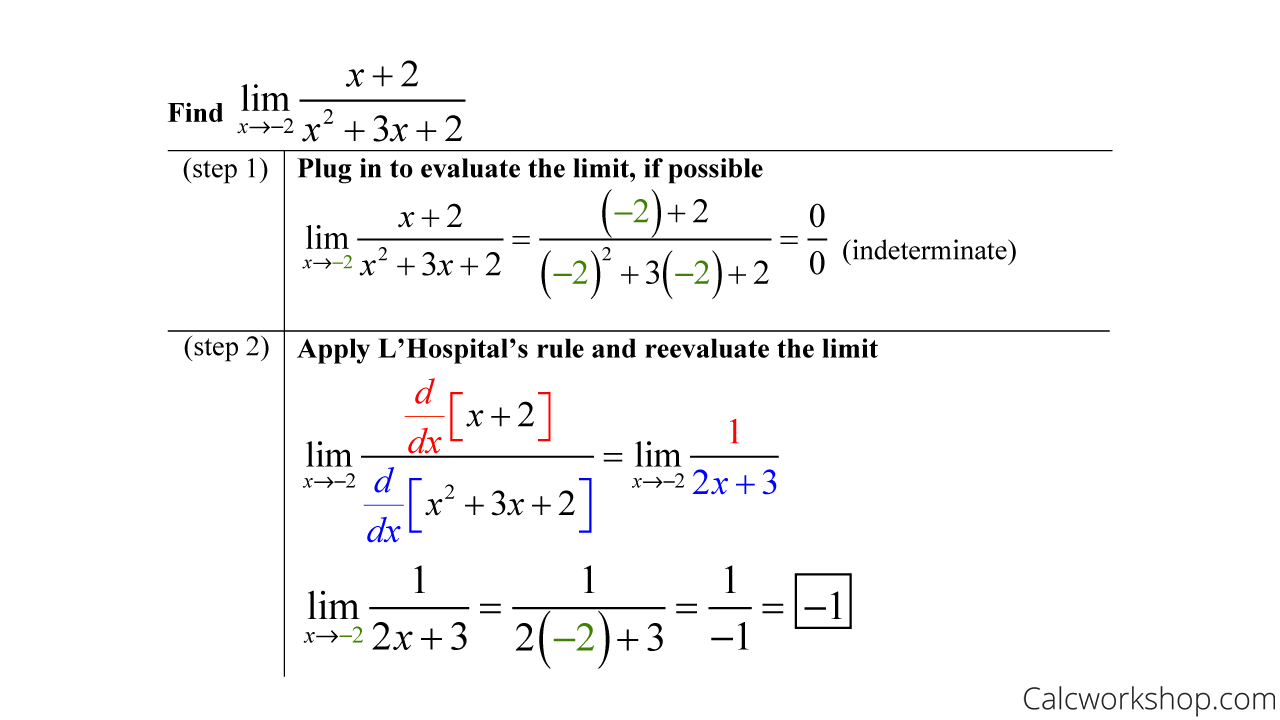
Lhopitals Rule – Indeterminate – Divided By Zero
Notice that we could have just as easily factored the rational function and arrived at the same answer, but with L’Hopital’s rule, we achieved the same goal using derivatives.
Example
Alright, now let’s look at how we can use l’Hospital’s rule for the indeterminate form of infinity over infinity.
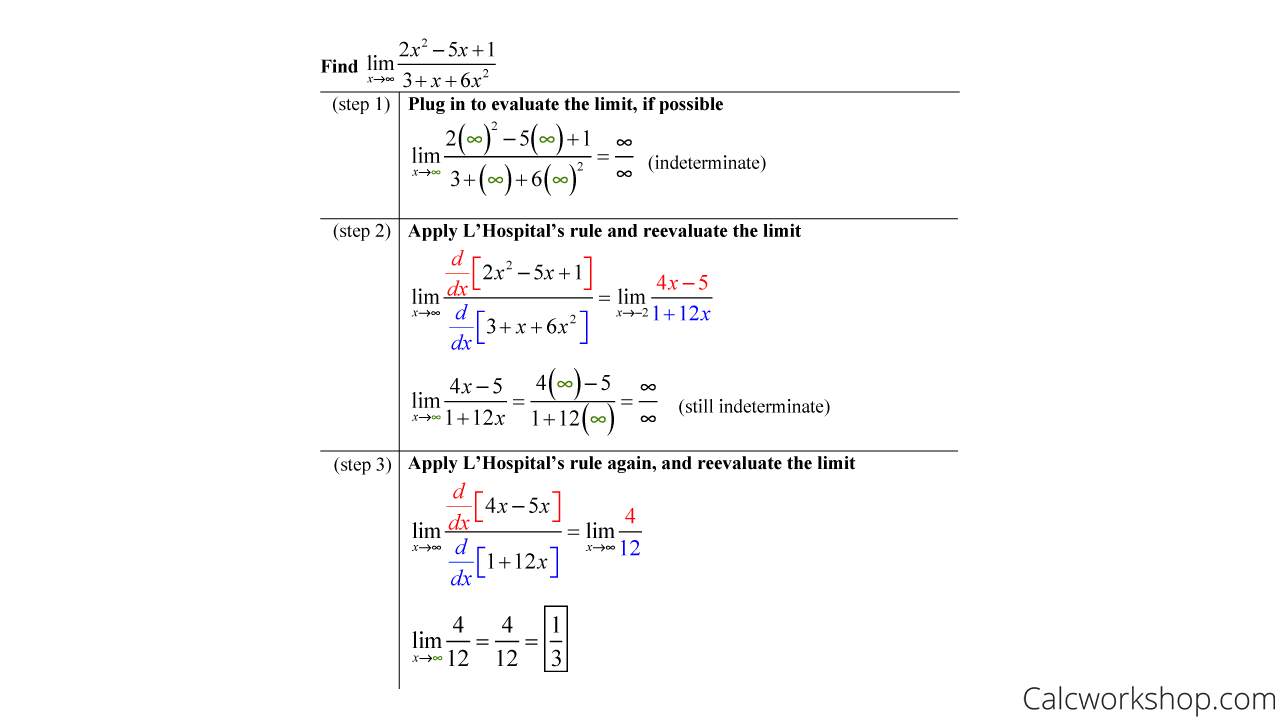
Lhopital Rule — Limit At Infinity
Observe that we had to apply L’Hopital’s rule twice to find the limit value.
But overall, the process is straightforward: if the limit is indeterminate, take the derivative of the top and the derivative of the bottom separately and then reevaluate the limit until you arrive at a defined value.
Simple!
Why Does L’hopital’s Rule Work
Okay, so without getting bogged down with semantics or the formal proof involving Cauchy’s Mean Value Theorem, let’s discuss why L’Hopital’s Rule works.
When I was studying calculus for the first time, this was the explanation given to me, and now I want to pass it along to you.
Suppose we are taking the limit of a function as x approaches infinity and whose numerator and denominator subsequently approach infinity as well.
This means the limit of this algebraic fraction is indeterminate, and the limit doesn’t give us a clear picture of what is happening.
Is the numerator rapidly approaching infinity while the denominator is going to infinity more slowly? Or is the denominator speeding toward infinity, and the numerator is lagging behind? In other words, who is dominating the behavior of the overall limit? Is it the numerator or denominator?
Hmm, if only there were a way to observe their individual rate of change, then we can see which function is the dominant function.
Wait, that’s it!
Rather than just comparing the numerator and denominator directly, let’s compare their derivatives (i.e., rate of change)!
And this is the idea behind L’Hospital’s Rule!
By comparing the rate of change, we can easily decipher the function’s behavior as a whole.
Advanced Problems
Okay, so now let’s look at a few examples of more advanced forms of indeterminate forms and see how l’Hospital’s rule really because invaluable.
Example
First, we will look at an example of an indeterminate product.
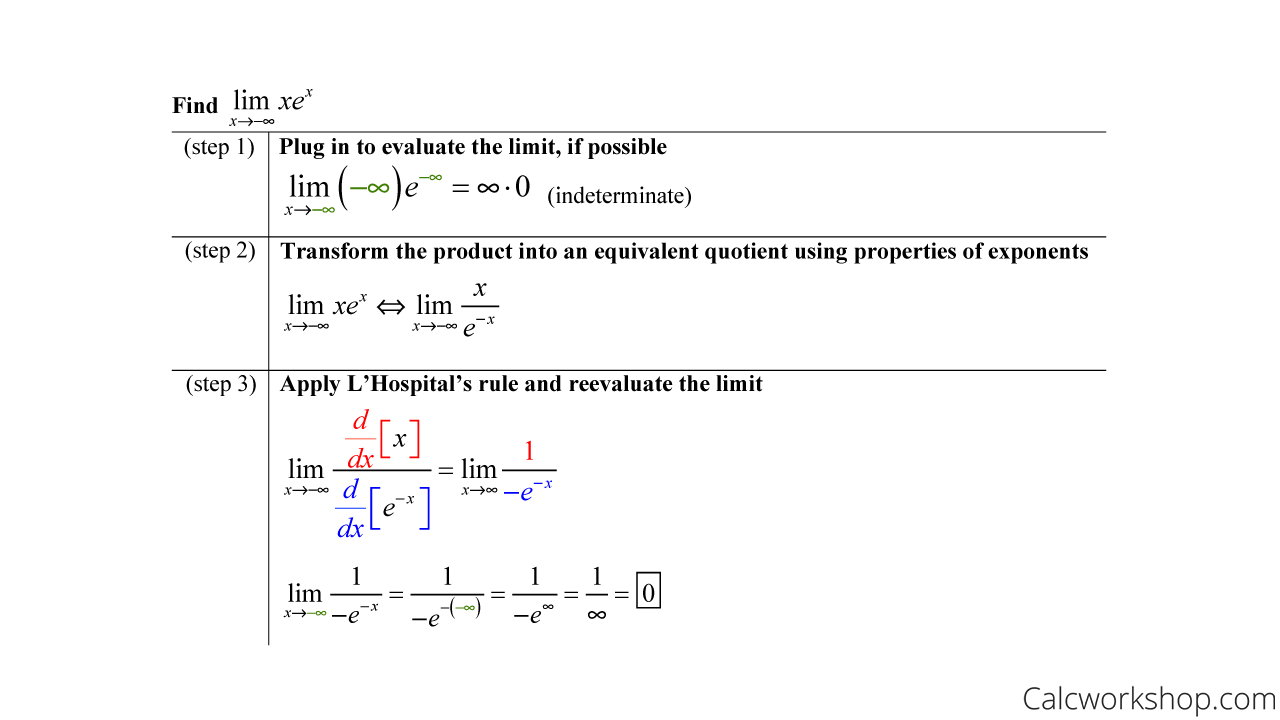
Indeterminate Limit — Infinity Times Zero
Example
The next type of limit we will look at is called an indeterminate difference.
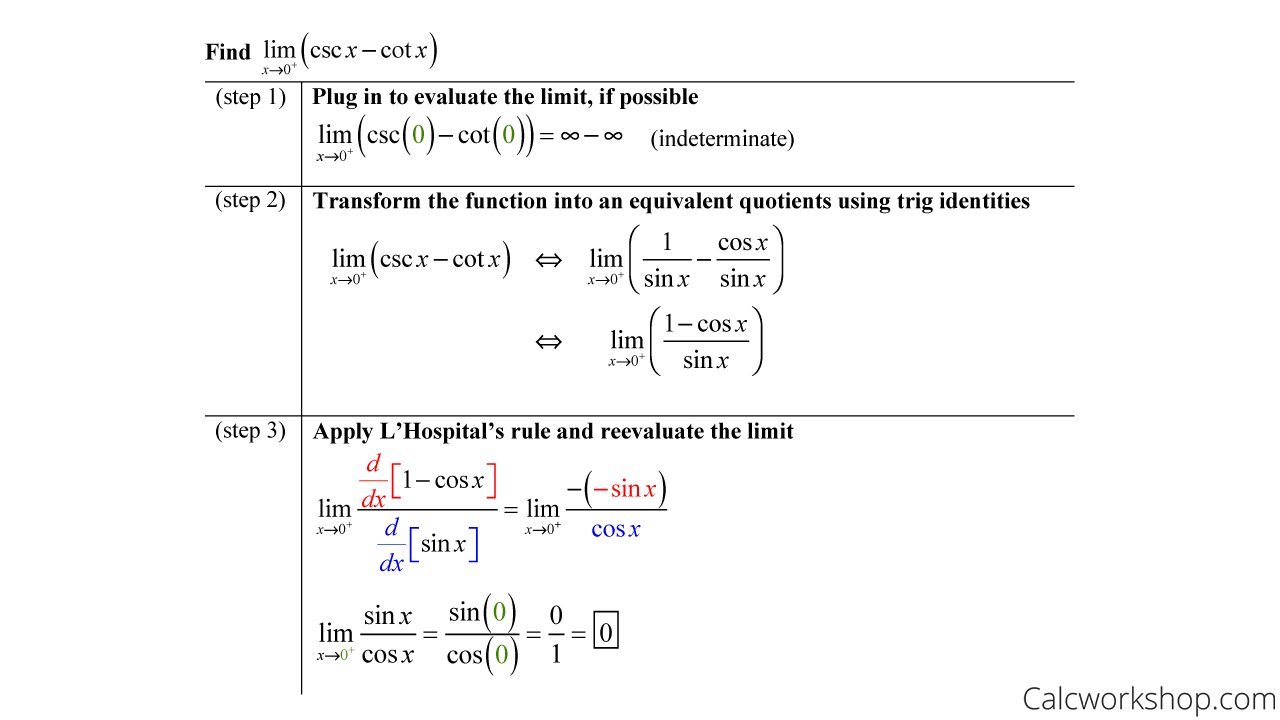
L Hospital Rule — Trig
Example
Our last example is when indeterminate powers arise. These types of questions are the most challenging as they require logarithms’ properties.
\begin{equation}
\text { Find } \lim _{x \rightarrow 0^{+}}(\sin x)^{\tan x}
\end{equation}Step 1: Plug in to evaluate the limit, if possible.
\begin{equation}
\lim _{x \rightarrow 0^{+}}(\sin (0))^{\tan (0)}=0^{0}
\end{equation}Step 2: Transform the function by taking the natural logarithmic of both sides and change the product into a quotient.
\begin{equation}
\begin{aligned}
&y=(\sin x)^{\tan x} \\
&\ln y=\ln (\sin x)^{\tan x} \\
&\ln y=\tan x \cdot \ln (\sin x) \\
&\ln y=\frac{1}{\cot x} \cdot \ln (\sin x) \\
&\ln y=\frac{\ln (\sin x)}{\cot x}
\end{aligned}
\end{equation}Step 3: Apply L’Hospital’s rule.
\begin{equation}
\begin{aligned}
&\ln y=\lim _{x \rightarrow 0^{+}} \frac{\ln (\sin x)}{\cot x} \\
&\ln y=\lim _{x \rightarrow 0^{+}} \frac{\frac{d}{d x}[\ln (\sin x)]}{\frac{d}{d x}[\cot x]}=\lim _{x \rightarrow 0^{+}} \frac{\left(\frac{\cos x}{\sin x}\right)}{-\csc ^{2} x} \\
&\ln y=\lim _{x \rightarrow 0^{+}} \frac{\left(\frac{\cos x}{\sin x}\right)}{-\csc ^{2} x}=\lim _{x \rightarrow 0^{+}}(-\cos x \cdot \sin x)=(-\cos (0) \cdot \sin (0))=-1 \cdot 0=0
\end{aligned}
\end{equation}Step 4: Exponentiate both sides of the equation to solve for y.
\begin{equation}
\begin{aligned}
&\ln y=0 \\
&e^{\ln y}=e^{0} \\
&y=e^{0}=1
\end{aligned}
\end{equation}
Super cool — but sneaky!
So, together we will work through various problems in detail and quickly discover how L’Hopitals Rule enables us to find limits of indeterminate forms.
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.